Refine search
Actions for selected content:
9062 results in Discrete Mathematics, Information Theory and Coding
Chapter 8 - More about Permanents
-
- Book:
- Permanents
- Published online:
- 05 June 2013
- Print publication:
- 28 December 1984, pp 129-160
-
- Chapter
- Export citation
Chapter 10 - Congruence Properties of Partition Functions
-
- Book:
- The Theory of Partitions
- Published online:
- 10 February 2010
- Print publication:
- 28 December 1984, pp 159-178
-
- Chapter
- Export citation
Index
-
- Book:
- Permanents
- Published online:
- 05 June 2013
- Print publication:
- 28 December 1984, pp 203-205
-
- Chapter
- Export citation
Introduction
-
- Book:
- Measurement Theory
- Published online:
- 04 August 2010
- Print publication:
- 28 December 1984, pp 1-12
-
- Chapter
- Export citation
Editor's Statement
-
-
- Book:
- Measurement Theory
- Published online:
- 04 August 2010
- Print publication:
- 28 December 1984, pp xv-xvi
-
- Chapter
- Export citation
Chapter 13 - Partitions in Combinatorics
-
- Book:
- The Theory of Partitions
- Published online:
- 10 February 2010
- Print publication:
- 28 December 1984, pp 212-229
-
- Chapter
- Export citation
Chapter 6 - Upper Bounds for Permanents
-
- Book:
- Permanents
- Published online:
- 05 June 2013
- Print publication:
- 28 December 1984, pp 103-118
-
- Chapter
- Export citation
Chapter 2 - Infinite Series Generating Functions
-
- Book:
- The Theory of Partitions
- Published online:
- 10 February 2010
- Print publication:
- 28 December 1984, pp 16-32
-
- Chapter
- Export citation
Chapter 1 - Relations
-
- Book:
- Measurement Theory
- Published online:
- 04 August 2010
- Print publication:
- 28 December 1984, pp 13-48
-
- Chapter
- Export citation
Author Index
-
- Book:
- Measurement Theory
- Published online:
- 04 August 2010
- Print publication:
- 28 December 1984, pp 405-410
-
- Chapter
- Export citation
Chapter 4 - Applications to Psychophysical Scaling
-
- Book:
- Measurement Theory
- Published online:
- 04 August 2010
- Print publication:
- 28 December 1984, pp 149-196
-
- Chapter
- Export citation
Bibliography
-
- Book:
- Permanents
- Published online:
- 05 June 2013
- Print publication:
- 28 December 1984, pp 161-196
-
- Chapter
- Export citation
Chapter 7 - Evaluation of Permanents
-
- Book:
- Permanents
- Published online:
- 05 June 2013
- Print publication:
- 28 December 1984, pp 119-128
-
- Chapter
- Export citation
Author Index
-
- Book:
- The Theory of Partitions
- Published online:
- 10 February 2010
- Print publication:
- 28 December 1984, pp 250-251
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- The Theory of Partitions
- Published online:
- 10 February 2010
- Print publication:
- 28 December 1984, pp i-v
-
- Chapter
- Export citation
Chapter 1 - The Theory of Permanents in the Historical Order of Development
-
- Book:
- Permanents
- Published online:
- 05 June 2013
- Print publication:
- 28 December 1984, pp 1-14
-
- Chapter
- Export citation
Chapter 5 - The Hardy–Ramanujan–Rademacher Expansion of p(n)
-
- Book:
- The Theory of Partitions
- Published online:
- 10 February 2010
- Print publication:
- 28 December 1984, pp 68-87
-
- Chapter
- Export citation
Detecting algebraic K-theory
- Part of
-
- Journal:
- Mathematika / Volume 31 / Issue 2 / December 1984
- Published online by Cambridge University Press:
- 26 February 2010, pp. 234-244
- Print publication:
- December 1984
-
- Article
- Export citation
On the oscillation of solutions of linear differential equations
- Part of
-
- Journal:
- Mathematika / Volume 31 / Issue 2 / December 1984
- Published online by Cambridge University Press:
- 26 February 2010, pp. 214-226
- Print publication:
- December 1984
-
- Article
- Export citation
Theories for the diffraction of three-dimensional surface waves by plane vertical obstacles
- Part of
-
- Journal:
- Mathematika / Volume 31 / Issue 2 / December 1984
- Published online by Cambridge University Press:
- 26 February 2010, pp. 178-195
- Print publication:
- December 1984
-
- Article
- Export citation
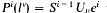 , to
, to