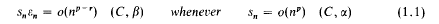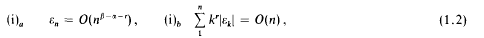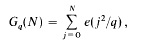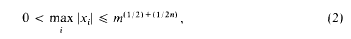Refine search
Actions for selected content:
9062 results in Discrete Mathematics, Information Theory and Coding
Chapter III - The Hyperelliptic Equation
-
- Book:
- Diophantine Equations over Function Fields
- Published online:
- 05 April 2013
- Print publication:
- 26 April 1984, pp 29-47
-
- Chapter
- Export citation
Chapter IV - Equations of Small Genus
-
- Book:
- Diophantine Equations over Function Fields
- Published online:
- 05 April 2013
- Print publication:
- 26 April 1984, pp 48-64
-
- Chapter
- Export citation
References
-
- Book:
- Diophantine Equations over Function Fields
- Published online:
- 05 April 2013
- Print publication:
- 26 April 1984, pp 124-125
-
- Chapter
- Export citation
Chapter VIII - The Superelliptic Equation
-
- Book:
- Diophantine Equations over Function Fields
- Published online:
- 05 April 2013
- Print publication:
- 26 April 1984, pp 117-123
-
- Chapter
- Export citation
Chapter II - The Thue Equation
-
- Book:
- Diophantine Equations over Function Fields
- Published online:
- 05 April 2013
- Print publication:
- 26 April 1984, pp 17-28
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Diophantine Equations over Function Fields
- Published online:
- 05 April 2013
- Print publication:
- 26 April 1984, pp i-vi
-
- Chapter
- Export citation
MTK volume 30 issue 2 Front matter
-
- Journal:
- Mathematika / Volume 30 / Issue 2 / December 1983
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f10
- Print publication:
- December 1983
-
- Article
-
- You have access
- Export citation
The toroidal analogue to Eberhard's theorem
-
- Journal:
- Mathematika / Volume 30 / Issue 2 / December 1983
- Published online by Cambridge University Press:
- 26 February 2010, pp. 274-290
- Print publication:
- December 1983
-
- Article
- Export citation
Convergence and summability factors in a sequence (II)
- Part of
-
- Journal:
- Mathematika / Volume 30 / Issue 2 / December 1983
- Published online by Cambridge University Press:
- 26 February 2010, pp. 255-273
- Print publication:
- December 1983
-
- Article
- Export citation
The graphs of exponential sums
-
- Journal:
- Mathematika / Volume 30 / Issue 2 / December 1983
- Published online by Cambridge University Press:
- 26 February 2010, pp. 153-163
- Print publication:
- December 1983
-
- Article
- Export citation
MTK volume 30 issue 2 Back matter
-
- Journal:
- Mathematika / Volume 30 / Issue 2 / December 1983
- Published online by Cambridge University Press:
- 26 February 2010, p. b1
- Print publication:
- December 1983
-
- Article
-
- You have access
- Export citation
Aspherical manifolds with the Q-homology of a sphere
-
- Journal:
- Mathematika / Volume 30 / Issue 2 / December 1983
- Published online by Cambridge University Press:
- 26 February 2010, pp. 291-294
- Print publication:
- December 1983
-
- Article
- Export citation
On a free boundary problem for the equations of tidal motions
- Part of
-
- Journal:
- Mathematika / Volume 30 / Issue 2 / December 1983
- Published online by Cambridge University Press:
- 26 February 2010, pp. 222-254
- Print publication:
- December 1983
-
- Article
- Export citation
K-analytic sets
- Part of
-
- Journal:
- Mathematika / Volume 30 / Issue 2 / December 1983
- Published online by Cambridge University Press:
- 26 February 2010, pp. 189-221
- Print publication:
- December 1983
-
- Article
- Export citation
Small solutions of congruences
-
- Journal:
- Mathematika / Volume 30 / Issue 2 / December 1983
- Published online by Cambridge University Press:
- 26 February 2010, pp. 164-188
- Print publication:
- December 1983
-
- Article
- Export citation
IRREGULARITIES OF PARTITIONS: RAMSEY THEORY, UNIFORM DISTRIBUTION
-
-
- Book:
- Surveys in Combinatorics
- Published online:
- 05 May 2013
- Print publication:
- 11 August 1983, pp 201-246
-
- Chapter
- Export citation
REDFIELD DISCOVERED AGAIN
-
-
- Book:
- Surveys in Combinatorics
- Published online:
- 05 May 2013
- Print publication:
- 11 August 1983, pp 135-156
-
- Chapter
- Export citation
MAXIMUM SETS IN FINITE PROJECTIVE SPACES
-
-
- Book:
- Surveys in Combinatorics
- Published online:
- 05 May 2013
- Print publication:
- 11 August 1983, pp 55-76
-
- Chapter
- Export citation
GL(n, C) FOR COMBINATORIALISTS
-
-
- Book:
- Surveys in Combinatorics
- Published online:
- 05 May 2013
- Print publication:
- 11 August 1983, pp 187-200
-
- Chapter
- Export citation
BOUNDS ON PERMANENTS, AND THE NUMBER OF 1-FACTORS AND 1-FACTORIZATIONS OF BIPARTITE GRAPHS
-
-
- Book:
- Surveys in Combinatorics
- Published online:
- 05 May 2013
- Print publication:
- 11 August 1983, pp 107-134
-
- Chapter
- Export citation