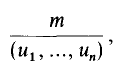Refine search
Actions for selected content:
9011 results in Discrete Mathematics, Information Theory and Coding
Power mean values of the Riemann zeta-function
-
- Journal:
- Mathematika / Volume 29 / Issue 2 / December 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 202-212
- Print publication:
- December 1982
-
- Article
- Export citation
MTK volume 29 issue 2 Front matter
-
- Journal:
- Mathematika / Volume 29 / Issue 2 / December 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- December 1982
-
- Article
-
- You have access
- Export citation
The recognition of certain Hausdorff like measures
- Part of
-
- Journal:
- Mathematika / Volume 29 / Issue 2 / December 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 260-263
- Print publication:
- December 1982
-
- Article
- Export citation
Slices of L. Fejes Tóth's sausage conjecture
- Part of
-
- Journal:
- Mathematika / Volume 29 / Issue 2 / December 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 194-201
- Print publication:
- December 1982
-
- Article
- Export citation
On the Mertens conjecture for cusp forms
-
- Journal:
- Mathematika / Volume 29 / Issue 2 / December 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 213-226
- Print publication:
- December 1982
-
- Article
- Export citation
Exponential sums connected with Ramanujan's function τ(n)
-
- Journal:
- Mathematika / Volume 29 / Issue 2 / December 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 270-277
- Print publication:
- December 1982
-
- Article
- Export citation
Local cohomology and modules of generalized fractions
- Part of
-
- Journal:
- Mathematika / Volume 29 / Issue 2 / December 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 296-306
- Print publication:
- December 1982
-
- Article
- Export citation
MTK volume 29 issue 1 Front matter
-
- Journal:
- Mathematika / Volume 29 / Issue 1 / June 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- June 1982
-
- Article
-
- You have access
- Export citation
Totally ordered measure spaces and their Lp algebras
- Part of
-
- Journal:
- Mathematika / Volume 29 / Issue 1 / June 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 42-54
- Print publication:
- June 1982
-
- Article
- Export citation
On the representation of even integers as sums of two almost-primes in algebraic number fields
-
- Journal:
- Mathematika / Volume 29 / Issue 1 / June 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 93-108
- Print publication:
- June 1982
-
- Article
- Export citation
A measure invariant under group endomorphisms
- Part of
-
- Journal:
- Mathematika / Volume 29 / Issue 1 / June 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 116-118
- Print publication:
- June 1982
-
- Article
- Export citation
On the presentation of stratified sets and singular varieties
- Part of
-
- Journal:
- Mathematika / Volume 29 / Issue 1 / June 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 135-170
- Print publication:
- June 1982
-
- Article
- Export citation
Covering and packing properties of bounded sequences of convex sets
-
- Journal:
- Mathematika / Volume 29 / Issue 1 / June 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 18-31
- Print publication:
- June 1982
-
- Article
- Export citation
Mean values of superharmonic functions on half-spaces
-
- Journal:
- Mathematika / Volume 29 / Issue 1 / June 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 55-57
- Print publication:
- June 1982
-
- Article
- Export citation
A parity problem from sieve theory
-
- Journal:
- Mathematika / Volume 29 / Issue 1 / June 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-6
- Print publication:
- June 1982
-
- Article
- Export citation
Sets of finite sets satisfying union conditions
-
- Journal:
- Mathematika / Volume 29 / Issue 1 / June 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 128-134
- Print publication:
- June 1982
-
- Article
- Export citation
Hausdorff dimension and the exceptional set of projections
- Part of
-
- Journal:
- Mathematika / Volume 29 / Issue 1 / June 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 109-115
- Print publication:
- June 1982
-
- Article
- Export citation
Cubic Diophantine inequalities
-
- Journal:
- Mathematika / Volume 29 / Issue 1 / June 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 83-92
- Print publication:
- June 1982
-
- Article
- Export citation
Boundary measures of solutions of partial differential equations
- Part of
-
- Journal:
- Mathematika / Volume 29 / Issue 1 / June 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 67-82
- Print publication:
- June 1982
-
- Article
- Export citation
Modules of generalized fractions
- Part of
-
- Journal:
- Mathematika / Volume 29 / Issue 1 / June 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 32-41
- Print publication:
- June 1982
-
- Article
- Export citation
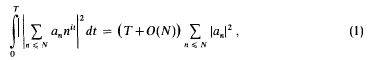
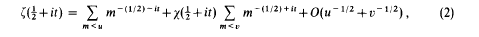
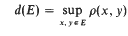
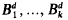 be
be 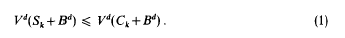
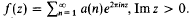 We assume further that
We assume further that 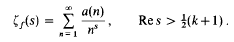
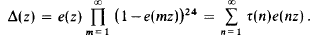
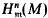 may be viewed as a module of generalized fractions of
may be viewed as a module of generalized fractions of 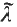 on Ĩ such that τ(
on Ĩ such that τ(