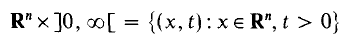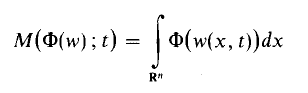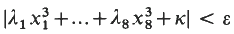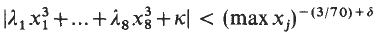Refine search
Actions for selected content:
9084 results in Discrete Mathematics, Information Theory and Coding
MTK volume 29 issue 1 Front matter
-
- Journal:
- Mathematika / Volume 29 / Issue 1 / June 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- June 1982
-
- Article
-
- You have access
- Export citation
Totally ordered measure spaces and their Lp algebras
- Part of
-
- Journal:
- Mathematika / Volume 29 / Issue 1 / June 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 42-54
- Print publication:
- June 1982
-
- Article
- Export citation
On the representation of even integers as sums of two almost-primes in algebraic number fields
-
- Journal:
- Mathematika / Volume 29 / Issue 1 / June 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 93-108
- Print publication:
- June 1982
-
- Article
- Export citation
A measure invariant under group endomorphisms
- Part of
-
- Journal:
- Mathematika / Volume 29 / Issue 1 / June 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 116-118
- Print publication:
- June 1982
-
- Article
- Export citation
On the presentation of stratified sets and singular varieties
- Part of
-
- Journal:
- Mathematika / Volume 29 / Issue 1 / June 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 135-170
- Print publication:
- June 1982
-
- Article
- Export citation
Covering and packing properties of bounded sequences of convex sets
-
- Journal:
- Mathematika / Volume 29 / Issue 1 / June 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 18-31
- Print publication:
- June 1982
-
- Article
- Export citation
Mean values of superharmonic functions on half-spaces
-
- Journal:
- Mathematika / Volume 29 / Issue 1 / June 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 55-57
- Print publication:
- June 1982
-
- Article
- Export citation
A parity problem from sieve theory
-
- Journal:
- Mathematika / Volume 29 / Issue 1 / June 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-6
- Print publication:
- June 1982
-
- Article
- Export citation
Sets of finite sets satisfying union conditions
-
- Journal:
- Mathematika / Volume 29 / Issue 1 / June 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 128-134
- Print publication:
- June 1982
-
- Article
- Export citation
Hausdorff dimension and the exceptional set of projections
- Part of
-
- Journal:
- Mathematika / Volume 29 / Issue 1 / June 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 109-115
- Print publication:
- June 1982
-
- Article
- Export citation
Cubic Diophantine inequalities
-
- Journal:
- Mathematika / Volume 29 / Issue 1 / June 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 83-92
- Print publication:
- June 1982
-
- Article
- Export citation
Boundary measures of solutions of partial differential equations
- Part of
-
- Journal:
- Mathematika / Volume 29 / Issue 1 / June 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 67-82
- Print publication:
- June 1982
-
- Article
- Export citation
Modules of generalized fractions
- Part of
-
- Journal:
- Mathematika / Volume 29 / Issue 1 / June 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 32-41
- Print publication:
- June 1982
-
- Article
- Export citation
Squarefree numbers on short intervals
-
- Journal:
- Mathematika / Volume 29 / Issue 1 / June 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 7-17
- Print publication:
- June 1982
-
- Article
- Export citation
Low-Reynolds-number flow between converging spheres
- Part of
-
- Journal:
- Mathematika / Volume 29 / Issue 1 / June 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 58-66
- Print publication:
- June 1982
-
- Article
- Export citation
Simplicial faces and sections of a convex polytope
-
- Journal:
- Mathematika / Volume 29 / Issue 1 / June 1982
- Published online by Cambridge University Press:
- 26 February 2010, pp. 119-127
- Print publication:
- June 1982
-
- Article
- Export citation
Cesàro means and recurrence in dynamic thermoelasticity
-
- Journal:
- Mathematika / Volume 28 / Issue 2 / December 1981
- Published online by Cambridge University Press:
- 26 February 2010, pp. 211-230
- Print publication:
- December 1981
-
- Article
- Export citation
Minimal width and diameter of lattice-point-free convex bodies
-
- Journal:
- Mathematika / Volume 28 / Issue 2 / December 1981
- Published online by Cambridge University Press:
- 26 February 2010, pp. 255-264
- Print publication:
- December 1981
-
- Article
- Export citation
Lifting properties and uniform regularity of lebesgue measures on topological spaces
- Part of
-
- Journal:
- Mathematika / Volume 28 / Issue 2 / December 1981
- Published online by Cambridge University Press:
- 26 February 2010, pp. 198-205
- Print publication:
- December 1981
-
- Article
- Export citation
Convex bodies which tile space by translation: Acknowledgement of priority
-
- Journal:
- Mathematika / Volume 28 / Issue 2 / December 1981
- Published online by Cambridge University Press:
- 26 February 2010, p. 191
- Print publication:
- December 1981
-
- Article
- Export citation
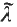 on Ĩ such that τ(
on Ĩ such that τ(