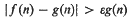Refine search
Actions for selected content:
9032 results in Discrete Mathematics, Information Theory and Coding
Index
-
- Book:
- Parallelisms of Complete Designs
- Published online:
- 16 March 2010
- Print publication:
- 10 June 1976, pp 143-144
-
- Chapter
- Export citation
3 - Steiner points and Veblen points
-
- Book:
- Parallelisms of Complete Designs
- Published online:
- 16 March 2010
- Print publication:
- 10 June 1976, pp 46-62
-
- Chapter
- Export citation
2 - The parallelogram property
-
- Book:
- Parallelisms of Complete Designs
- Published online:
- 16 March 2010
- Print publication:
- 10 June 1976, pp 19-45
-
- Chapter
- Export citation
6 - Automorphism groups
-
- Book:
- Parallelisms of Complete Designs
- Published online:
- 16 March 2010
- Print publication:
- 10 June 1976, pp 108-128
-
- Chapter
- Export citation
Introduction
-
- Book:
- Parallelisms of Complete Designs
- Published online:
- 16 March 2010
- Print publication:
- 10 June 1976, pp 1-3
-
- Chapter
- Export citation
Contents
-
- Book:
- Parallelisms of Complete Designs
- Published online:
- 16 March 2010
- Print publication:
- 10 June 1976, pp iii-iv
-
- Chapter
- Export citation
Electrostatic sieve
-
- Journal:
- Mathematika / Volume 23 / Issue 1 / June 1976
- Published online by Cambridge University Press:
- 26 February 2010, pp. 51-56
- Print publication:
- June 1976
-
- Article
- Export citation
On approximation with algebraic numbers of bounded degree
-
- Journal:
- Mathematika / Volume 23 / Issue 1 / June 1976
- Published online by Cambridge University Press:
- 26 February 2010, pp. 18-31
- Print publication:
- June 1976
-
- Article
- Export citation
On a problem of hardy and ramanujan
-
- Journal:
- Mathematika / Volume 23 / Issue 1 / June 1976
- Published online by Cambridge University Press:
- 26 February 2010, pp. 10-17
- Print publication:
- June 1976
-
- Article
- Export citation
On the distribution of primes in short intervals
-
- Journal:
- Mathematika / Volume 23 / Issue 1 / June 1976
- Published online by Cambridge University Press:
- 26 February 2010, pp. 4-9
- Print publication:
- June 1976
-
- Article
-
- You have access
- Export citation
An approximation property of certain nonlinear Volterra integral operators
- Part of
-
- Journal:
- Mathematika / Volume 23 / Issue 1 / June 1976
- Published online by Cambridge University Press:
- 26 February 2010, pp. 45-50
- Print publication:
- June 1976
-
- Article
- Export citation
The 2-adic density of a quadratic form
-
- Journal:
- Mathematika / Volume 23 / Issue 1 / June 1976
- Published online by Cambridge University Press:
- 26 February 2010, pp. 94-106
- Print publication:
- June 1976
-
- Article
- Export citation
Pipeflows distorted by non-symmetric indentation or branching
- Part of
-
- Journal:
- Mathematika / Volume 23 / Issue 1 / June 1976
- Published online by Cambridge University Press:
- 26 February 2010, pp. 62-83
- Print publication:
- June 1976
-
- Article
- Export citation
On non-Archimedean lengths in groups
- Part of
-
- Journal:
- Mathematika / Volume 23 / Issue 1 / June 1976
- Published online by Cambridge University Press:
- 26 February 2010, pp. 57-61
- Print publication:
- June 1976
-
- Article
- Export citation
On the spectra of singular elliptic operators
- Part of
-
- Journal:
- Mathematika / Volume 23 / Issue 1 / June 1976
- Published online by Cambridge University Press:
- 26 February 2010, pp. 107-115
- Print publication:
- June 1976
-
- Article
- Export citation
A variant of the fundamental theorem of projective geometry
-
- Journal:
- Mathematika / Volume 23 / Issue 1 / June 1976
- Published online by Cambridge University Press:
- 26 February 2010, pp. 89-93
- Print publication:
- June 1976
-
- Article
- Export citation
The stability of an evolving two-dimensional vortex sheet
- Part of
-
- Journal:
- Mathematika / Volume 23 / Issue 1 / June 1976
- Published online by Cambridge University Press:
- 26 February 2010, pp. 35-44
- Print publication:
- June 1976
-
- Article
- Export citation
Axiomatic characterisations of dimension
- Part of
-
- Journal:
- Mathematika / Volume 23 / Issue 1 / June 1976
- Published online by Cambridge University Press:
- 26 February 2010, pp. 84-88
- Print publication:
- June 1976
-
- Article
- Export citation
MTK volume 23 issue 1 Front matter
-
- Journal:
- Mathematika / Volume 23 / Issue 1 / June 1976
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- June 1976
-
- Article
-
- You have access
- Export citation
On l-class groups of certain number fields
-
- Journal:
- Mathematika / Volume 23 / Issue 1 / June 1976
- Published online by Cambridge University Press:
- 26 February 2010, pp. 116-123
- Print publication:
- June 1976
-
- Article
- Export citation
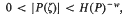
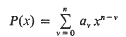
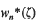 for the supremum of the exponents
for the supremum of the exponents