Refine search
Actions for selected content:
9032 results in Discrete Mathematics, Information Theory and Coding
Note on the slow rotation of a concave spherical lens or bowl in two immiscible semi-infinite viscous fluids
- Part of
-
- Journal:
- Mathematika / Volume 21 / Issue 1 / June 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 147-154
- Print publication:
- June 1974
-
- Article
- Export citation
Problems related to a conjecture by Grünbaum
- Part of
-
- Journal:
- Mathematika / Volume 21 / Issue 1 / June 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 45-54
- Print publication:
- June 1974
-
- Article
- Export citation
A Problem of Erdős and Kátai
-
- Journal:
- Mathematika / Volume 21 / Issue 1 / June 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 110-113
- Print publication:
- June 1974
-
- Article
- Export citation
On asymmetry classes of convex bodies
- Part of
-
- Journal:
- Mathematika / Volume 21 / Issue 1 / June 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 12-18
- Print publication:
- June 1974
-
- Article
- Export citation
On maximal simplices inscribed in a central convex set
- Part of
-
- Journal:
- Mathematika / Volume 21 / Issue 1 / June 1974
- Published online by Cambridge University Press:
- 26 February 2010, pp. 38-44
- Print publication:
- June 1974
-
- Article
- Export citation
13 - The Tutte polynomial
-
- Book:
- Algebraic Graph Theory
- Published online:
- 05 August 2012
- Print publication:
- 16 May 1974, pp 97-105
-
- Chapter
- Export citation
5 - Spanning trees and associated structures
-
- Book:
- Algebraic Graph Theory
- Published online:
- 05 August 2012
- Print publication:
- 16 May 1974, pp 31-37
-
- Chapter
- Export citation
18 - Symmetric graphs of degree three
-
- Book:
- Algebraic Graph Theory
- Published online:
- 05 August 2012
- Print publication:
- 16 May 1974, pp 138-148
-
- Chapter
- Export citation
23 - Minimal regular graphs with given girth
-
- Book:
- Algebraic Graph Theory
- Published online:
- 05 August 2012
- Print publication:
- 16 May 1974, pp 180-190
-
- Chapter
- Export citation
4 - Cycles and cuts
-
- Book:
- Algebraic Graph Theory
- Published online:
- 05 August 2012
- Print publication:
- 16 May 1974, pp 23-30
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Algebraic Graph Theory
- Published online:
- 05 August 2012
- Print publication:
- 16 May 1974, pp i-iv
-
- Chapter
- Export citation
7 - Deteminant expansions
-
- Book:
- Algebraic Graph Theory
- Published online:
- 05 August 2012
- Print publication:
- 16 May 1974, pp 44-51
-
- Chapter
- Export citation
16 - Vertex-transitive graphs
-
- Book:
- Algebraic Graph Theory
- Published online:
- 05 August 2012
- Print publication:
- 16 May 1974, pp 122-129
-
- Chapter
- Export citation
11 - The multiplicative expansion
-
- Book:
- Algebraic Graph Theory
- Published online:
- 05 August 2012
- Print publication:
- 16 May 1974, pp 81-88
-
- Chapter
- Export citation
PART ONE - LINEAR ALGEBRA IN GRAPH THEORY
-
- Book:
- Algebraic Graph Theory
- Published online:
- 05 August 2012
- Print publication:
- 16 May 1974, pp 5-6
-
- Chapter
- Export citation
PART THREE - SYMMETRY AND REGULARITY
-
- Book:
- Algebraic Graph Theory
- Published online:
- 05 August 2012
- Print publication:
- 16 May 1974, pp 113-114
-
- Chapter
- Export citation
PART TWO - COLOURING PROBLEMS
-
- Book:
- Algebraic Graph Theory
- Published online:
- 05 August 2012
- Print publication:
- 16 May 1974, pp 61-62
-
- Chapter
- Export citation
12 - The induced subgraph expansion
-
- Book:
- Algebraic Graph Theory
- Published online:
- 05 August 2012
- Print publication:
- 16 May 1974, pp 89-96
-
- Chapter
- Export citation
9 - The chromatic polynomial
-
- Book:
- Algebraic Graph Theory
- Published online:
- 05 August 2012
- Print publication:
- 16 May 1974, pp 63-72
-
- Chapter
- Export citation
20 - Distance-transitive graphs
-
- Book:
- Algebraic Graph Theory
- Published online:
- 05 August 2012
- Print publication:
- 16 May 1974, pp 155-163
-
- Chapter
- Export citation
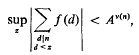
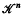 denote the set of all convex bodies in
denote the set of all convex bodies in