Refine search
Actions for selected content:
9032 results in Discrete Mathematics, Information Theory and Coding
On self-induced separation II
-
- Journal:
- Mathematika / Volume 20 / Issue 1 / June 1973
- Published online by Cambridge University Press:
- 26 February 2010, pp. 98-108
- Print publication:
- June 1973
-
- Article
- Export citation
Isomorphic Koszul complexes
-
- Journal:
- Mathematika / Volume 20 / Issue 1 / June 1973
- Published online by Cambridge University Press:
- 26 February 2010, pp. 53-58
- Print publication:
- June 1973
-
- Article
- Export citation
Bending of a thin semi-circular plate elastically restrained along the circular edge and clamped along the diameter
-
- Journal:
- Mathematika / Volume 20 / Issue 1 / June 1973
- Published online by Cambridge University Press:
- 26 February 2010, pp. 34-46
- Print publication:
- June 1973
-
- Article
- Export citation
Bochner's theorem and mean-field electrodynamics
-
- Journal:
- Mathematika / Volume 20 / Issue 1 / June 1973
- Published online by Cambridge University Press:
- 26 February 2010, pp. 24-33
- Print publication:
- June 1973
-
- Article
- Export citation
MTK volume 20 issue 1 Front matter
-
- Journal:
- Mathematika / Volume 20 / Issue 1 / June 1973
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- June 1973
-
- Article
-
- You have access
- Export citation
A theorem on the structure of cell–decompositions of orientable 2–manifolds
-
- Journal:
- Mathematika / Volume 20 / Issue 1 / June 1973
- Published online by Cambridge University Press:
- 26 February 2010, pp. 63-82
- Print publication:
- June 1973
-
- Article
- Export citation
An application of a reduction method of R. Rado to the study of common transversals
-
- Journal:
- Mathematika / Volume 20 / Issue 1 / June 1973
- Published online by Cambridge University Press:
- 26 February 2010, pp. 83-86
- Print publication:
- June 1973
-
- Article
- Export citation
The divisors of p-1
-
- Journal:
- Mathematika / Volume 20 / Issue 1 / June 1973
- Published online by Cambridge University Press:
- 26 February 2010, pp. 87-97
- Print publication:
- June 1973
-
- Article
- Export citation
An effective lower bound on the “Diophantine approximation” of algebraic functions by rational functions
-
- Journal:
- Mathematika / Volume 20 / Issue 1 / June 1973
- Published online by Cambridge University Press:
- 26 February 2010, pp. 4-15
- Print publication:
- June 1973
-
- Article
- Export citation
On the K-theory of the quaternion group
-
- Journal:
- Mathematika / Volume 20 / Issue 1 / June 1973
- Published online by Cambridge University Press:
- 26 February 2010, pp. 59-62
- Print publication:
- June 1973
-
- Article
- Export citation
Difference covers which have small k-sums for any k
-
- Journal:
- Mathematika / Volume 20 / Issue 1 / June 1973
- Published online by Cambridge University Press:
- 26 February 2010, pp. 109-118
- Print publication:
- June 1973
-
- Article
- Export citation
On the Euler characteristic of spherical polyhedra and the Euler relation
- Part of
-
- Journal:
- Mathematika / Volume 19 / Issue 2 / December 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. 139-143
- Print publication:
- December 1972
-
- Article
- Export citation
The number of plane trees
- Part of
-
- Journal:
- Mathematika / Volume 19 / Issue 2 / December 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. 200-204
- Print publication:
- December 1972
-
- Article
- Export citation
Sections and projections of convex polytopes
-
- Journal:
- Mathematika / Volume 19 / Issue 2 / December 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. 144-162
- Print publication:
- December 1972
-
- Article
- Export citation
Index to volume 19
-
- Journal:
- Mathematika / Volume 19 / Issue 2 / December 1972
- Published online by Cambridge University Press:
- 26 February 2010, p. 244
- Print publication:
- December 1972
-
- Article
- Export citation
The largest subset in [1,n] whose integers have pairwise l.c.m. not exceeding n
-
- Journal:
- Mathematika / Volume 19 / Issue 2 / December 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. 221-230
- Print publication:
- December 1972
-
- Article
- Export citation
Projecting and uniformising Borel sets with
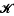 σ, sections I.
σ, sections I.
-
- Journal:
- Mathematika / Volume 19 / Issue 2 / December 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. 231-243
- Print publication:
- December 1972
-
- Article
- Export citation
Sphere packings constructed from BCH and Justesen codes
-
- Journal:
- Mathematika / Volume 19 / Issue 2 / December 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. 183-190
- Print publication:
- December 1972
-
- Article
- Export citation
An integral-geometric meaning for lower order area functions of convex bodies
- Part of
-
- Journal:
- Mathematika / Volume 19 / Issue 2 / December 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. 205-212
- Print publication:
- December 1972
-
- Article
- Export citation
On duct flow of a linear viscoelastic fluid
- Part of
-
- Journal:
- Mathematika / Volume 19 / Issue 2 / December 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. 180-182
- Print publication:
- December 1972
-
- Article
- Export citation
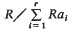
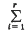
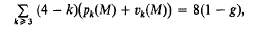
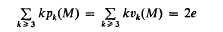
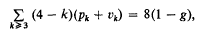
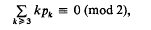
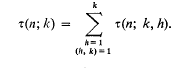
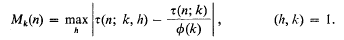
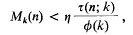
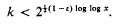
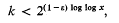
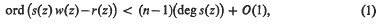
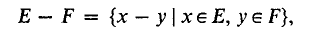
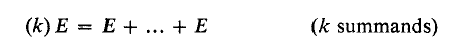
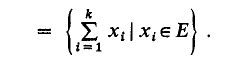
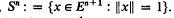 . It is convenient to introduce the (–1)-dimensional sphere
. It is convenient to introduce the (–1)-dimensional sphere 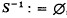 , where
, where 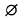 denotes the empty set. By an
denotes the empty set. By an  is the unique (–1)-dimensional subsphere of
is the unique (–1)-dimensional subsphere of 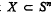 , we understand the intersection of all subspheres of
, we understand the intersection of all subspheres of 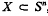 , with respect to
, with respect to 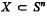 with respect to the usual topology sphZ
with respect to the usual topology sphZ 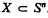 . For
. For 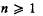 each (
each (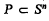 is called a closed (spherical) polytope, if it is the intersection of finitely many closed hemispheres, and, if, in addition, it does not contain a subsphere of
is called a closed (spherical) polytope, if it is the intersection of finitely many closed hemispheres, and, if, in addition, it does not contain a subsphere of 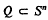 is called an
is called an 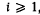 , or shortly an
, or shortly an 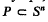 such that dim
such that dim 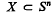 is called a closed polyhedron, if it is a finite union of closed polytopes
is called a closed polyhedron, if it is a finite union of closed polytopes 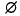 is the only (–1)-dimensional closed polyhedron of S
is the only (–1)-dimensional closed polyhedron of S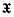 the set of all closed polyhedra of S
the set of all closed polyhedra of S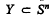 is called an
is called an 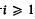 , if there are finitely many
, if there are finitely many 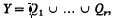 , and dim
, and dim 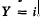 . By
. By 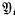 we denote the set of all
we denote the set of all 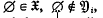 for all
for all 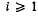 , and each
, and each 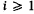 , belongs to
, belongs to 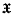 and to
and to 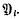 , For each
, For each 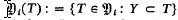 . A map
. A map  is defined by
is defined by 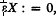 , for all
, for all 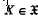 , and, for all
, and, for all 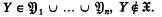 .
.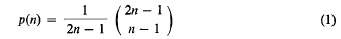
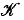 is a subcomplex of the boundary complex ℬ (
is a subcomplex of the boundary complex ℬ (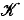 is homeomorphic to an (
is homeomorphic to an (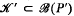 corresponding to
corresponding to 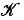 is a shadow boundary of
is a shadow boundary of 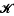
 is made up of all those figures from a certain class which support, in some sense, a convex body. Further, the examples lead us to expect that measures of this kind will appear as integrals of densities which may depend on the choices of
is made up of all those figures from a certain class which support, in some sense, a convex body. Further, the examples lead us to expect that measures of this kind will appear as integrals of densities which may depend on the choices of 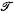 . Here we treat a question of the type just described: to determine a measure for sets of
. Here we treat a question of the type just described: to determine a measure for sets of 