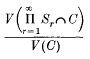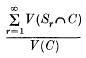Refine search
Actions for selected content:
9032 results in Discrete Mathematics, Information Theory and Coding
On the unsteady motion of a rotating fluid in a cavity
-
- Journal:
- Mathematika / Volume 12 / Issue 1 / June 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 97-106
- Print publication:
- June 1965
-
- Article
- Export citation
A theorem on convex kernels
-
- Journal:
- Mathematika / Volume 12 / Issue 1 / June 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 89-93
- Print publication:
- June 1965
-
- Article
- Export citation
Cubic Diophantine equations: a supplementary congruence condition
-
- Journal:
- Mathematika / Volume 12 / Issue 1 / June 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 39-48
- Print publication:
- June 1965
-
- Article
- Export citation
On badly approximable numbers
-
- Journal:
- Mathematika / Volume 12 / Issue 1 / June 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 10-20
- Print publication:
- June 1965
-
- Article
- Export citation
Metrics for sets of convex bodies
-
- Journal:
- Mathematika / Volume 12 / Issue 1 / June 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 73-88
- Print publication:
- June 1965
-
- Article
- Export citation
On irredundant components of the kernel of an ideal
-
- Journal:
- Mathematika / Volume 12 / Issue 1 / June 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 65-72
- Print publication:
- June 1965
-
- Article
- Export citation
Plasticity theory and multipolar continuum mechanics
-
- Journal:
- Mathematika / Volume 12 / Issue 1 / June 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 21-26
- Print publication:
- June 1965
-
- Article
- Export citation
Eigen-functions for the strip problem
-
- Journal:
- Mathematika / Volume 12 / Issue 1 / June 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. 58-64
- Print publication:
- June 1965
-
- Article
- Export citation
MTK volume 12 issue 1 Cover and Front matter
-
- Journal:
- Mathematika / Volume 12 / Issue 1 / June 1965
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f4
- Print publication:
- June 1965
-
- Article
-
- You have access
- Export citation
The second moment of the complexity of a graph
-
- Journal:
- Mathematika / Volume 11 / Issue 2 / December 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. 95-98
- Print publication:
- December 1964
-
- Article
- Export citation
MTK volume 11 issue 2 Front matter
-
- Journal:
- Mathematika / Volume 11 / Issue 2 / December 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- December 1964
-
- Article
-
- You have access
- Export citation
A mixed boundary value problem of two-dimensional elasticity theory
-
- Journal:
- Mathematika / Volume 11 / Issue 2 / December 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. 151-154
- Print publication:
- December 1964
-
- Article
- Export citation
Index to volume 11
-
- Journal:
- Mathematika / Volume 11 / Issue 2 / December 1964
- Published online by Cambridge University Press:
- 26 February 2010, p. 185
- Print publication:
- December 1964
-
- Article
- Export citation
Cubic congruences
-
- Journal:
- Mathematika / Volume 11 / Issue 2 / December 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. 142-150
- Print publication:
- December 1964
-
- Article
- Export citation
A note on a problem of littlewood about diophantine approximation
-
- Journal:
- Mathematika / Volume 11 / Issue 2 / December 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. 137-141
- Print publication:
- December 1964
-
- Article
- Export citation
The stresses in an infinite strip containing a circular inclusion
-
- Journal:
- Mathematika / Volume 11 / Issue 2 / December 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. 155-170
- Print publication:
- December 1964
-
- Article
- Export citation
The number of plane trees with a given partition
-
- Journal:
- Mathematika / Volume 11 / Issue 2 / December 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. 99-101
- Print publication:
- December 1964
-
- Article
- Export citation
The amount of overlapping in partial coverings of space by equal spheres
-
- Journal:
- Mathematika / Volume 11 / Issue 2 / December 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. 171-184
- Print publication:
- December 1964
-
- Article
- Export citation
A note on the cyclotomic polynomial
-
- Journal:
- Mathematika / Volume 11 / Issue 2 / December 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. 131-136
- Print publication:
- December 1964
-
- Article
- Export citation
The effect of diffusion in the mean wind direction in atmospheric turbulence
-
- Journal:
- Mathematika / Volume 11 / Issue 2 / December 1964
- Published online by Cambridge University Press:
- 26 February 2010, pp. 119-124
- Print publication:
- December 1964
-
- Article
- Export citation
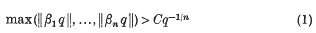
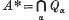 is called the
is called the 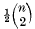 No moments higher than the first were known in general and they remarked in [4] that even “the second would be worth knowing”. The main object in this paper is to derive a formula for the second moment of
No moments higher than the first were known in general and they remarked in [4] that even “the second would be worth knowing”. The main object in this paper is to derive a formula for the second moment of