Refine search
Actions for selected content:
9032 results in Discrete Mathematics, Information Theory and Coding
On Kloosterman's sum
-
- Journal:
- Mathematika / Volume 8 / Issue 1 / June 1961
- Published online by Cambridge University Press:
- 26 February 2010, pp. 83-86
- Print publication:
- June 1961
-
- Article
- Export citation
MTK volume 8 issue 1 Front matter
-
- Journal:
- Mathematika / Volume 8 / Issue 1 / June 1961
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- June 1961
-
- Article
-
- You have access
- Export citation
A note on the maximum resultant shear in the aeolotropic torsion problem
-
- Journal:
- Mathematika / Volume 8 / Issue 1 / June 1961
- Published online by Cambridge University Press:
- 26 February 2010, pp. 79-82
- Print publication:
- June 1961
-
- Article
- Export citation
On two-centred expansions in cylindrical polar co-ordinates
-
- Journal:
- Mathematika / Volume 8 / Issue 1 / June 1961
- Published online by Cambridge University Press:
- 26 February 2010, pp. 69-78
- Print publication:
- June 1961
-
- Article
- Export citation
Cauchy problem for the generalised radially symmetric wave equation
-
- Journal:
- Mathematika / Volume 8 / Issue 1 / June 1961
- Published online by Cambridge University Press:
- 26 February 2010, pp. 66-68
- Print publication:
- June 1961
-
- Article
- Export citation
A note on binary cubic forms
-
- Journal:
- Mathematika / Volume 8 / Issue 1 / June 1961
- Published online by Cambridge University Press:
- 26 February 2010, pp. 58-62
- Print publication:
- June 1961
-
- Article
- Export citation
Completely aeolotropic cylinders under general lateral loading
-
- Journal:
- Mathematika / Volume 8 / Issue 1 / June 1961
- Published online by Cambridge University Press:
- 26 February 2010, pp. 45-54
- Print publication:
- June 1961
-
- Article
- Export citation
The real cubic case of Mahler's conjecture
-
- Journal:
- Mathematika / Volume 8 / Issue 1 / June 1961
- Published online by Cambridge University Press:
- 26 February 2010, pp. 55-57
- Print publication:
- June 1961
-
- Article
- Export citation
Indefinite quadratic Diophantine equations
-
- Journal:
- Mathematika / Volume 8 / Issue 1 / June 1961
- Published online by Cambridge University Press:
- 26 February 2010, pp. 32-38
- Print publication:
- June 1961
-
- Article
- Export citation
Note on a conjecture of L. A. Santaló
-
- Journal:
- Mathematika / Volume 8 / Issue 1 / June 1961
- Published online by Cambridge University Press:
- 26 February 2010, pp. 63-65
- Print publication:
- June 1961
-
- Article
- Export citation
Functions continuous and singular with respect to a Hausdorff measure
-
- Journal:
- Mathematika / Volume 8 / Issue 1 / June 1961
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-31
- Print publication:
- June 1961
-
- Article
- Export citation
Indefinite quadratic polynomials
-
- Journal:
- Mathematika / Volume 7 / Issue 2 / December 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. 141-144
- Print publication:
- December 1960
-
- Article
- Export citation
Green's functions for thin perforated elastic slabs
-
- Journal:
- Mathematika / Volume 7 / Issue 2 / December 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. 101-112
- Print publication:
- December 1960
-
- Article
- Export citation
Certain subgroups of free products
-
- Journal:
- Mathematika / Volume 7 / Issue 2 / December 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. 117-124
- Print publication:
- December 1960
-
- Article
- Export citation
Some elastic and thermoelastic stress distributions in a semi-infinite solid
-
- Journal:
- Mathematika / Volume 7 / Issue 2 / December 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. 149-160
- Print publication:
- December 1960
-
- Article
- Export citation
On a theorem of P. J. Cohen
-
- Journal:
- Mathematika / Volume 7 / Issue 2 / December 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. 93-97
- Print publication:
- December 1960
-
- Article
- Export citation
On a theorem of Mahler
-
- Journal:
- Mathematika / Volume 7 / Issue 2 / December 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. 139-140
- Print publication:
- December 1960
-
- Article
- Export citation
An application of Jensen's formula to polynomials
-
- Journal:
- Mathematika / Volume 7 / Issue 2 / December 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. 98-100
- Print publication:
- December 1960
-
- Article
- Export citation
Index to volume 7
-
- Journal:
- Mathematika / Volume 7 / Issue 2 / December 1960
- Published online by Cambridge University Press:
- 26 February 2010, p. 172
- Print publication:
- December 1960
-
- Article
- Export citation
Inequalities between mixed volumes of convex sets
-
- Journal:
- Mathematika / Volume 7 / Issue 2 / December 1960
- Published online by Cambridge University Press:
- 26 February 2010, pp. 125-138
- Print publication:
- December 1960
-
- Article
- Export citation

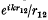 This work formed an extension to that of Carlson and Rushbrooke [2] (also Buehler and Hirschfelder [3]) on the Coulomb Green's function and arose out of considerations of the interaction energy of two charge distributions taking account of electromagnetic retardation. The two-centred expansion obtained in [1] took the form of a double Taylor series, each term being interpreted as a Maxwell multipole—multipole interaction energy between two “charge” distributions coupled through a retarded scalar field. The first few terms in the expansion were also given in spherical polar coordinates.
This work formed an extension to that of Carlson and Rushbrooke [2] (also Buehler and Hirschfelder [3]) on the Coulomb Green's function and arose out of considerations of the interaction energy of two charge distributions taking account of electromagnetic retardation. The two-centred expansion obtained in [1] took the form of a double Taylor series, each term being interpreted as a Maxwell multipole—multipole interaction energy between two “charge” distributions coupled through a retarded scalar field. The first few terms in the expansion were also given in spherical polar coordinates.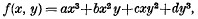

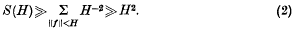
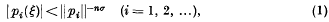
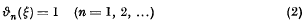
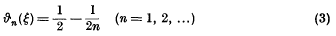
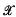 be a plane bounded convex set whose width in the direction φ is
be a plane bounded convex set whose width in the direction φ is 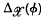 . It has been shown by L. A. Santaló that
. It has been shown by L. A. Santaló that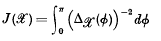
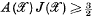 and that equality characterizes triangles. In this note Santaló's conjecture is shown to be true.
and that equality characterizes triangles. In this note Santaló's conjecture is shown to be true.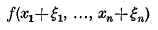
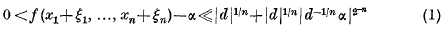
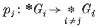 may be defined by requiring it to be trivial on
may be defined by requiring it to be trivial on 
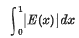

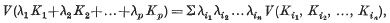
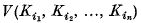 may be chosen to be positive and symmetric in their arguments
may be chosen to be positive and symmetric in their arguments 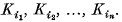 These coefficients, which are
These coefficients, which are 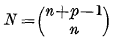 in number, are called the
in number, are called the 