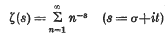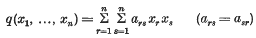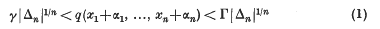Refine search
Actions for selected content:
9032 results in Discrete Mathematics, Information Theory and Coding
Stress distribution in a notched plate
-
- Journal:
- Mathematika / Volume 4 / Issue 1 / June 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 76-96
- Print publication:
- June 1957
-
- Article
- Export citation
A note on coverings
-
- Journal:
- Mathematika / Volume 4 / Issue 1 / June 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 1-6
- Print publication:
- June 1957
-
- Article
- Export citation
A note on form rings and ideals
-
- Journal:
- Mathematika / Volume 4 / Issue 1 / June 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 51-60
- Print publication:
- June 1957
-
- Article
- Export citation
Bounded representations of integers by quadratic forms
-
- Journal:
- Mathematika / Volume 4 / Issue 1 / June 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 17-24
- Print publication:
- June 1957
-
- Article
- Export citation
Multiple covering of the plane by circles
-
- Journal:
- Mathematika / Volume 4 / Issue 1 / June 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 7-16
- Print publication:
- June 1957
-
- Article
- Export citation
A note on summability factors
-
- Journal:
- Mathematika / Volume 4 / Issue 1 / June 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 25-40
- Print publication:
- June 1957
-
- Article
- Export citation
MTK volume 4 issue 1 Front matter
-
- Journal:
- Mathematika / Volume 4 / Issue 1 / June 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f3
- Print publication:
- June 1957
-
- Article
-
- You have access
- Export citation
The Green's function of an elliptic plate
-
- Journal:
- Mathematika / Volume 4 / Issue 1 / June 1957
- Published online by Cambridge University Press:
- 26 February 2010, pp. 61-69
- Print publication:
- June 1957
-
- Article
- Export citation
The spread of a matrix
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 127-130
- Print publication:
- December 1956
-
- Article
- Export citation
Dilational and distortional vibrations of semi-infinite solids and plates
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 153-163
- Print publication:
- December 1956
-
- Article
- Export citation
On a result of Marshall Hall
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 109-110
- Print publication:
- December 1956
-
- Article
- Export citation
MTK volume 3 issue 2 Front matter
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- December 1956
-
- Article
-
- You have access
- Export citation
Note on irregularities of distribution
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 131-135
- Print publication:
- December 1956
-
- Article
- Export citation
Measurable almost periodic functions
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 140-143
- Print publication:
- December 1956
-
- Article
- Export citation
Indefinite quadratic forms in many variables
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 81-101
- Print publication:
- December 1956
-
- Article
- Export citation
Semi-regular local rings
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 117-126
- Print publication:
- December 1956
-
- Article
- Export citation
Thin circular plates under certain distributions of normal loading
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 144-152
- Print publication:
- December 1956
-
- Article
- Export citation
Extended computation of the Riemann zeta-function
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 102-108
- Print publication:
- December 1956
-
- Article
- Export citation
Indefinite quadratic polynomials in n variables
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, pp. 111-116
- Print publication:
- December 1956
-
- Article
- Export citation
Index to volume 3
-
- Journal:
- Mathematika / Volume 3 / Issue 2 / December 1956
- Published online by Cambridge University Press:
- 26 February 2010, p. 164
- Print publication:
- December 1956
-
- Article
- Export citation

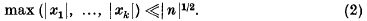
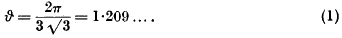
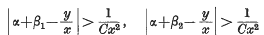
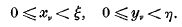
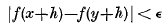
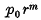 cos nϑ(or sin
cos nϑ(or sin