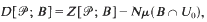Refine search
Actions for selected content:
9062 results in Discrete Mathematics, Information Theory and Coding
Long mollifiers of the Riemann Zeta-function
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 1 / June 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 71-87
- Print publication:
- June 1993
-
- Article
- Export citation
On the distribution of gaps between squarefree numbers
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 1 / June 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 88-101
- Print publication:
- June 1993
-
- Article
- Export citation
Multiple Franel integrals
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 1 / June 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 51-70
- Print publication:
- June 1993
-
- Article
- Export citation
The total curvature of a smooth closed curve in En is an upper bound to the total swing of its position vector
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 1 / June 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 148-151
- Print publication:
- June 1993
-
- Article
- Export citation
W. A. Adkins and S. H. Weintraub. Algebra, An Approach via Module Theory. Springer. 1992, 526 pp., DM88. - V. I. Arnol'd. Singularities of Caustics and Wave Fronts. Kluwer. 1990, 259 pp., £56. - V. I. Arnol'd. Catastrophy Theory. Springer. 1992, 150 pp., DM 38. - D. K. Arrowsmith and C. M. Place. Dynamical Systems. Differential Equations, Maps and Chaotic Behaviour. Chapman & Hall. 1992, 330 pp., £17·95 - D. J. Bell. Mathematics of Linear and Nonlinear Systems—for Engineers and Applied Scientists. Clarendon Press. 1991, 304 pp., £16·50 - M. Bognár. Foundations of Linking Theory. Akadémiai Kiadó, Budapest. 1992, 164 pp., $20. - Y. A. Brychkov, H.-J. Glaeske, A. P. Prudnikov and Vu Kim Tuan. Multidimensional Integral Transformations. Gordon and Breach. 1992, 386 pp., £44. - C. K. Chui. An Introduction to Wavelets. Academic Press. 1992, 264 pp., $49.95. - C. K. Chui. Editor. Wavelets: a Tutorial in Theory and Applications. Academic Press. 1992, 713 pp., $69.95 - J. Dieudonné. Mathematics—the Music of Reason. Springer. 1992, 287 pp., DM 68. - P. Drábek. Solvability and Bifurcations of Nonlinear Equations. Longman. 1992, 227 pp., £25. - A. Dzhuraev. Degenerate and other Problems. Longman. 1992, 316 pp., £56. - A. Dzhuraev. Methods of Singular Integral Equations. Longman. 1992, 311 pp., £56. - R. Henstock. The General Theory of Integration. Clarendon Press. 1991, 262 pp., £40. - P. N. Hoffman and J. F. Humphreys. Projective Representations of the Symmetric Group, Q-functions and Shifted Tableaux. Clarendon Press. 1992, 304 pp., £40. - B. R. Gelbaum. Problems in Real and Complex Analysis. Springer. 1992, 488 pp., DM 118. - J. Gregory and C. Lin. Constrained Optimization in the Calculus of Variations and Optimal Control Theory. Van Nostrand Reinhold. 1992, 217 pp., £39. - G. R. Grimmett and D. R. Stirzaker. Probability and Random Processes, 2nd edition. Clarendon Press. 1992, 541 pp., £22·50. Probability and Random Processes: Problems and Solutions. Clarendon Press. 1991, 356 pp., £19·50. - A. R. Hall. Isaac Newton: Adventurer in Thought. Blackwell. 1992, 468 pp., £19·95. - P. M. Harman and A. E. Shapiro. Editors. The Investigation of Difficult Things: Essays on Newton and the History of the Exact Sciences. Cambridge University Press. 1992, 531 pp., £90 - G. G. Joseph. The Crest of the Peacock: non-European Roots of Mathematics. Penguin. 1992, 371 pp., £8·99. - Johannes Kepler. New Astronomy. Translated by W. H. Donohue. Cambridge. 1992, 665 pp., £85. - V. V. Kharchenko. Automorphisms and Derivations of Associative Rings. Kluwer. 1991, 385 pp., £88. - Li Ta-Tsien and Chen Yunmei. Global Classical Solutions for Nonlinear Evolution Equations. Longman. 1992, 209 pp., £47. - G. Micula and P. Pavel. Differential and Integral Equations through Practical Problems and Exercises. Kluwer. 1992, 395 pp., £82. - H.-O. Peitgen, H. Jürgens and D. Saupe. Chaos and Fractals. Springer. 1992, 984 pp., DM98. - L. W. Tung. Japanese/English, English/Japanese Glossary of Scientific and Technical Terms. Wiley. 1993, 1146 pp., £56. - P. Wesseling. An Introduction to Multigrid Methods. Wiley. 1992, 284 pp., £49.
-
- Journal:
- Mathematika / Volume 40 / Issue 1 / June 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 153-159
- Print publication:
- June 1993
-
- Article
- Export citation
On the starting process of strongly nonlinear vortex/Rayleigh-wave interactions
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 1 / June 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 7-29
- Print publication:
- June 1993
-
- Article
- Export citation
Irregularities of point distribution relative to half-planes I
- Part of
-
- Journal:
- Mathematika / Volume 40 / Issue 1 / June 1993
- Published online by Cambridge University Press:
- 26 February 2010, pp. 102-126
- Print publication:
- June 1993
-
- Article
- Export citation
2 - The Four Colour Problem
-
- Book:
- The Petersen Graph
- Published online:
- 13 March 2010
- Print publication:
- 22 April 1993, pp 49-78
-
- Chapter
- Export citation
1 - The Petersen graph
-
- Book:
- The Petersen Graph
- Published online:
- 13 March 2010
- Print publication:
- 22 April 1993, pp 1-48
-
- Chapter
- Export citation
Notation Index
-
- Book:
- The Petersen Graph
- Published online:
- 13 March 2010
- Print publication:
- 22 April 1993, pp 343-344
-
- Chapter
- Export citation
4 - Factors
-
- Book:
- The Petersen Graph
- Published online:
- 13 March 2010
- Print publication:
- 22 April 1993, pp 112-153
-
- Chapter
- Export citation
Contents
-
- Book:
- The Petersen Graph
- Published online:
- 13 March 2010
- Print publication:
- 22 April 1993, pp v-viii
-
- Chapter
- Export citation
Conjecture Index
-
- Book:
- The Petersen Graph
- Published online:
- 13 March 2010
- Print publication:
- 22 April 1993, pp 340-342
-
- Chapter
- Export citation
5 - Beyond the Four Colour theorem
-
- Book:
- The Petersen Graph
- Published online:
- 13 March 2010
- Print publication:
- 22 April 1993, pp 154-182
-
- Chapter
- Export citation
8 - Symmetry
-
- Book:
- The Petersen Graph
- Published online:
- 13 March 2010
- Print publication:
- 22 April 1993, pp 249-278
-
- Chapter
- Export citation
6 - Cages
-
- Book:
- The Petersen Graph
- Published online:
- 13 March 2010
- Print publication:
- 22 April 1993, pp 183-213
-
- Chapter
- Export citation
Preface
-
- Book:
- The Petersen Graph
- Published online:
- 13 March 2010
- Print publication:
- 22 April 1993, pp ix-x
-
- Chapter
- Export citation
9 - The Petersen Graph in Diversity
-
- Book:
- The Petersen Graph
- Published online:
- 13 March 2010
- Print publication:
- 22 April 1993, pp 279-339
-
- Chapter
- Export citation
7 - Hypohamiltonian graphs
-
- Book:
- The Petersen Graph
- Published online:
- 13 March 2010
- Print publication:
- 22 April 1993, pp 214-248
-
- Chapter
- Export citation
3 - Snarks
-
- Book:
- The Petersen Graph
- Published online:
- 13 March 2010
- Print publication:
- 22 April 1993, pp 79-111
-
- Chapter
- Export citation
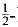 -line, where
-line, where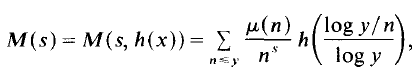
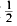 yields κ > 0·3562, having 0 < θ <
yields κ > 0·3562, having 0 < θ < 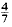 gives κ > 0·40219, and it is necessary to have θ > 0·165 in order to obtain a positive lower bound for κ. At present, it is known that the asymptotic formula remains valid for 0 < θ <
gives κ > 0·40219, and it is necessary to have θ > 0·165 in order to obtain a positive lower bound for κ. At present, it is known that the asymptotic formula remains valid for 0 < θ < 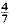 , this is due to Conrey. Without assuming the Riemann Hypothesis, Levinson's method provides the only known way of obtaining a positive lower bound for κ.
, this is due to Conrey. Without assuming the Riemann Hypothesis, Levinson's method provides the only known way of obtaining a positive lower bound for κ.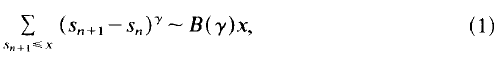
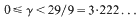
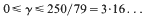

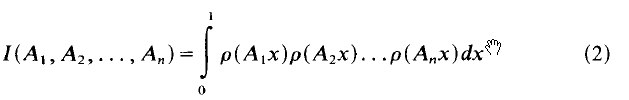
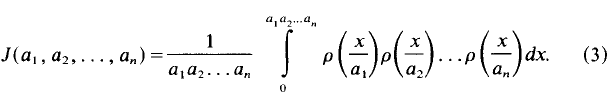
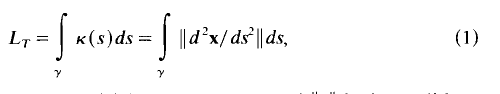

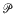 is a distribution of
is a distribution of