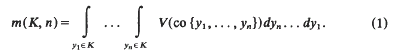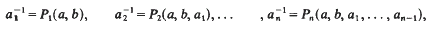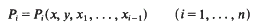Refine search
Actions for selected content:
9062 results in Discrete Mathematics, Information Theory and Coding
Frontmatter
-
- Book:
- The Petersen Graph
- Published online:
- 13 March 2010
- Print publication:
- 22 April 1993, pp i-iv
-
- Chapter
- Export citation
Index
-
- Book:
- The Petersen Graph
- Published online:
- 13 March 2010
- Print publication:
- 22 April 1993, pp 345-353
-
- Chapter
- Export citation
On the sausage catastrophe in 4-space
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 274-278
- Print publication:
- December 1992
-
- Article
- Export citation
R. P. Agarwal. Difference Equations and Inequalities: Theory, Methods and Applications. Marcel Dekker. 1992, 777 pp., $172.50. - V. I. Arnold. Ordinary Differential Equations. Springer. 1992, 334 pp., DM78. - Y. Boyarintsev. Methods for Solving Singular Systems of Ordinary Differential Equations. Wiley. 1992, 163 pp., £29·95. - W. E. Boyce and R. C. DiPrima. Elementary Differential Equations. 5th edition. Wiley. 1992, 544 pp., £55. - Y. Diers. Categories of Commutative Algebras. Clarendon Press. 1992, 271 pp., £40. - P. Erdős, Editor. Collected Papers of Paul Turan. Akademiai Kiado. 1990, 2665 pp. in three volumes, £125. - J. S. Golan. The Theory of Semirings, with Applications in Mathematics and Theoretical Computer Science. Longman. 1992, 318 pp., £58. - G. H. Golub and J. M. Ortega. Scientific Computing and Differential Equations. Academic Press. 1991, 337 pp., $49.95. - M. O. Gonzalez. Complex Analysis: Selected Topics. Marcel Dekker. 1992, 544 pp., $132.25. - K. R. Goodearl. Von Neumann Regular Rings. Krieger Publishing. 1991, 412 pp., $49.50. - M. Grinfeld. Thermodynamic Methods in the Theory of Heterogeneous Systems. Longman. 1991, 399 pp., £46. - J. Hale and H. Kocak. Dynamics and Bifurcations. Springer, 1991, 568 pp., DM98. - P. M. Higgins. Techniques of Semigroup Theory. Clarendon Press. 1992, 258 pp., £40. - D. G. Hoffman, D. A. Leonard, C. C. Lindner, K. T. Phelps, C. A. Rodger and J. R. Wall. Coding Theory—The Essentials. Marcel Dekker. 1991, 277 pp., $55. - W. W. J. Hulsbergen. Conjectures in Arithmetic and Algebraic Geometry. Wiley. 1992, 236 pp., £26·50. - K. Iwasaki, H. Kimura, S. Shimomura and M. Yoshida. From Gauss to Painlevé: A Modern Theory of Special Functions. Wiley. 1991, 347 pp., £31·95. - A. Jones, S. A. Morris and K. R. Pearson. Abstract Algebra and Famous Impossibilities. Springer. 1991, 187 pp., DM58. - I. Karatzas and S. E. Shreve. Brownian Motion and Stochastic Calculus. Second Edition. Springer. 1991, 470 pp., DM68. - J. Kondo. Integral Equations. Clarendon Press. 1991, 440 pp., £17·50. - T. Y. Lam. A First Course in Non-commutative Ring Theory. Springer. 1991, 397 pp., DM86. - R. E. O'MalleyJr., Singular Perturbation Methods for Ordinary Differential Equations. Springer. 1991, 225 pp., DM78. - A. P. Prudnikov, Y. A. Brychkov and O. I. Marichev. Integrals and Series. Volumes 4 and 5. Gordon & Breach. 1992, 618 pp. and 595 pp., £184 the pair. - K. W. Roggenkamp and M. J. Taylor. Group Rings and Class Groups. DMV Seminar Band 18. Birkhauser. 1992, 210 pp., 68 SFR. - W. A. Strauss. Partial Differential Equations. Wiley. 1992, 425 pp., £16·95. - N. J. Vilenkin and A. U. Klimyk. Representation of Lie Groups and Special Functions. Volume I: Simplest Lie Groups, Special Functions and Integral Transforms. Kluwer. 1991, 608 pp., £155. - D. Zwillinger. Handbook of Differential Equations. 2nd edition. Academic Press. 1992, 787 pp., $54·95.
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 422-427
- Print publication:
- December 1992
-
- Article
- Export citation
MTK volume 39 issue 2 Cover and Front matter
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. f1-f2
- Print publication:
- December 1992
-
- Article
-
- You have access
- Export citation
Two sharp inequalities for the norm of a factor of a polynomial
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 341-349
- Print publication:
- December 1992
-
- Article
- Export citation
On the k-HFD property in Dedekind domains with small class group
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 330-340
- Print publication:
- December 1992
-
- Article
- Export citation
A problem of Good on Hausdorff dimension
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 244-246
- Print publication:
- December 1992
-
- Article
- Export citation
The spatial distribution of algebraic integers on constant-norm hypersurfaces
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 350-366
- Print publication:
- December 1992
-
- Article
- Export citation
On the mean value of the area of a random polygon in a plane convex body
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 279-290
- Print publication:
- December 1992
-
- Article
- Export citation
Paradoxical decompositions using Lipschitz functions
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 216-222
- Print publication:
- December 1992
-
- Article
- Export citation
On the Busemann-Petty problem about convex, centrally symmetric bodies in ℝn
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 258-266
- Print publication:
- December 1992
-
- Article
- Export citation
Estimating sizes of a convex body by successive diameters and widths
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 247-257
- Print publication:
- December 1992
-
- Article
- Export citation
On the Lipschitz equivalence of Cantor sets
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 223-233
- Print publication:
- December 1992
-
- Article
- Export citation
On the exceptional set for the sum of a prime and a k-th power
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 400-421
- Print publication:
- December 1992
-
- Article
- Export citation
Speciality of full subalgebras and rational identities in Jordan algebras
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 327-329
- Print publication:
- December 1992
-
- Article
- Export citation
Index to volume 39
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 428-429
- Print publication:
- December 1992
-
- Article
- Export citation
Minimal pairs of convex bodies in two dimensions
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 267-273
- Print publication:
- December 1992
-
- Article
- Export citation
Regular and ubiquitous systems, and ℳs∞-dense sequences
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 234-243
- Print publication:
- December 1992
-
- Article
- Export citation
On the temporal evolution of finite ensembles
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 2 / December 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 291-318
- Print publication:
- December 1992
-
- Article
- Export citation
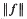 be the maximum of
be the maximum of 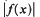 on the unit circle. We prove that
on the unit circle. We prove that 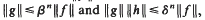 , where β =
, where β = 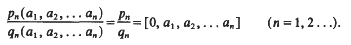
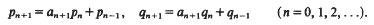
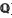 ] =
] = 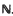 . Most of what we shall discuss is trivial when
. Most of what we shall discuss is trivial when 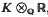 , and is to be regarded as a topological
, and is to be regarded as a topological 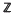 -algebra, dim
-algebra, dim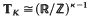 -submodule of rank
-submodule of rank 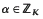 which have a fixed norm
which have a fixed norm