Refine search
Actions for selected content:
8126 results in Fluid dynamics and solid mechanics
2 - Tensor Calculus
-
- Book:
- A First Course in Continuum Mechanics
- Published online:
- 01 September 2010
- Print publication:
- 17 January 2008, pp 44-74
-
- Chapter
- Export citation
Preface
-
- Book:
- A First Course in Continuum Mechanics
- Published online:
- 01 September 2010
- Print publication:
- 17 January 2008, pp xv-xviii
-
- Chapter
- Export citation
5 - Balance Laws
-
- Book:
- A First Course in Continuum Mechanics
- Published online:
- 01 September 2010
- Print publication:
- 17 January 2008, pp 167-220
-
- Chapter
- Export citation
4 - Kinematics
-
- Book:
- A First Course in Continuum Mechanics
- Published online:
- 01 September 2010
- Print publication:
- 17 January 2008, pp 112-166
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- A First Course in Continuum Mechanics
- Published online:
- 01 September 2010
- Print publication:
- 17 January 2008, pp i-vi
-
- Chapter
- Export citation
Contents
-
- Book:
- A First Course in Continuum Mechanics
- Published online:
- 01 September 2010
- Print publication:
- 17 January 2008, pp vii-xiv
-
- Chapter
- Export citation
9 - Thermal Solid Mechanics
-
- Book:
- A First Course in Continuum Mechanics
- Published online:
- 01 September 2010
- Print publication:
- 17 January 2008, pp 355-385
-
- Chapter
- Export citation
Index
-
- Book:
- A First Course in Continuum Mechanics
- Published online:
- 01 September 2010
- Print publication:
- 17 January 2008, pp 390-394
-
- Chapter
- Export citation
7 - Isothermal Solid Mechanics
-
- Book:
- A First Course in Continuum Mechanics
- Published online:
- 01 September 2010
- Print publication:
- 17 January 2008, pp 271-323
-
- Chapter
- Export citation
1 - Tensor Algebra
-
- Book:
- A First Course in Continuum Mechanics
- Published online:
- 01 September 2010
- Print publication:
- 17 January 2008, pp 1-43
-
- Chapter
- Export citation
8 - Thermal Fluid Mechanics
-
- Book:
- A First Course in Continuum Mechanics
- Published online:
- 01 September 2010
- Print publication:
- 17 January 2008, pp 324-354
-
- Chapter
- Export citation
3 - Continuum Mass and Force Concepts
-
- Book:
- A First Course in Continuum Mechanics
- Published online:
- 01 September 2010
- Print publication:
- 17 January 2008, pp 75-111
-
- Chapter
- Export citation
6 - Isothermal Fluid Mechanics
-
- Book:
- A First Course in Continuum Mechanics
- Published online:
- 01 September 2010
- Print publication:
- 17 January 2008, pp 221-270
-
- Chapter
- Export citation
Bibliography
-
- Book:
- A First Course in Continuum Mechanics
- Published online:
- 01 September 2010
- Print publication:
- 17 January 2008, pp 386-389
-
- Chapter
- Export citation
SIGMOIDAL-TYPE SERIES EXPANSION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 3 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 431-450
-
- Article
-
- You have access
- Export citation
QUINTIC B-SPLINE COLLOCATION METHOD FOR NUMERICAL SOLUTION OF THE RLW EQUATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 3 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 389-410
-
- Article
-
- You have access
- Export citation
A SIMPLE DETERMINISTIC MODEL FOR VOLCANIC ASHFALL DEPOSITION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 3 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 325-336
-
- Article
-
- You have access
- Export citation
MODELLING OF GENERALIZED NEWTONIAN LID-DRIVEN CAVITY FLOW USING AN SPH METHOD
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 3 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 411-422
-
- Article
-
- You have access
- Export citation
VORTEX EQUILIBRIA IN FLOW PAST A PLATE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 3 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 347-359
-
- Article
-
- You have access
- Export citation
THREE NONNEGATIVE SOLUTIONS FOR SECOND-ORDER IMPULSIVE DIFFERENTIAL EQUATIONS WITH A THREE-POINT BOUNDARY VALUE PROBLEM
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 3 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 337-346
-
- Article
-
- You have access
- Export citation
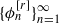 , where ϕ
, where ϕ