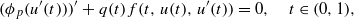Refine search
Actions for selected content:
8126 results in Fluid dynamics and solid mechanics
Abbreviations Used in This Book
-
- Book:
- Homogeneous Turbulence Dynamics
- Published online:
- 01 October 2009
- Print publication:
- 02 June 2008, pp xvi-xvi
-
- Chapter
- Export citation
2 - Statistical Analysis of Homogeneous Turbulent Flows: Reminders
-
- Book:
- Homogeneous Turbulence Dynamics
- Published online:
- 01 October 2009
- Print publication:
- 02 June 2008, pp 10-48
-
- Chapter
- Export citation
A COMPUTATIONAL METHOD FOR SOLVING TWO-DIMENSIONAL LINEAR FREDHOLM INTEGRAL EQUATIONS OF THE SECOND KIND
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 4 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 543-549
-
- Article
-
- You have access
- Export citation
COMPUTABLE STRONGLY ERGODIC RATES OF CONVERGENCE FOR CONTINUOUS-TIME MARKOV CHAINS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 4 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 463-478
-
- Article
-
- You have access
- Export citation
PERTURBATION THEORY FOR THE LU AND QR FACTORIZATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 4 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 451-461
-
- Article
-
- You have access
- Export citation
EXPANSION IN BELL POLYNOMIALS OF THE DISTRIBUTION OF THE TOTAL CLAIM AMOUNT WITH WEIBULL-DISTRIBUTED CLAIM SIZES
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 4 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 495-501
-
- Article
-
- You have access
- Export citation
SUCCESSIVE ITERATION AND POSITIVE SOLUTIONS FOR A p-LAPLACIAN MULTIPOINT BOUNDARY VALUE PROBLEM
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 4 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 551-560
-
- Article
-
- You have access
- Export citation
AN EVAPORATION HEAT ENGINE AND CONDENSATION HEAT PUMP
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 4 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 503-524
-
- Article
-
- You have access
- Export citation
SYMMETRY RESULT FOR SOME OVERDETERMINED VALUE PROBLEMS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 4 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 479-494
-
- Article
-
- You have access
- Export citation
ON FUNCTIONAL CENTRAL LIMIT THEOREMS FOR LINEAR RANDOM FIELDS WITH DEPENDENT INNOVATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 4 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 533-541
-
- Article
-
- You have access
- Export citation
GENERALIZED MIXED QUASI-COMPLEMENTARITY PROBLEMS IN TOPOLOGICAL VECTOR SPACES
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 4 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 525-531
-
- Article
-
- You have access
- Export citation
MISSILE CONTROL DESIGN BASED ON THE LINEAR MULTIPLE SLIDING MODE RECURSIVE METHOD
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 4 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 573-587
-
- Article
-
- You have access
- Export citation
A NOTE ON THE HU–HWANG–WANG CONJECTURE FOR GROUP TESTING
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 49 / Issue 4 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 561-571
-
- Article
-
- You have access
- Export citation
9 - DISCRETIZATION AND SOLUTION
-
- Book:
- Nonlinear Continuum Mechanics for Finite Element Analysis
- Published online:
- 06 July 2010
- Print publication:
- 13 March 2008, pp 237-265
-
- Chapter
- Export citation
Contents
-
- Book:
- Nonlinear Continuum Mechanics for Finite Element Analysis
- Published online:
- 06 July 2010
- Print publication:
- 13 March 2008, pp ix-xiv
-
- Chapter
- Export citation
8 - LINEARIZED EQUILIBRIUM EQUATIONS
-
- Book:
- Nonlinear Continuum Mechanics for Finite Element Analysis
- Published online:
- 06 July 2010
- Print publication:
- 13 March 2008, pp 216-236
-
- Chapter
- Export citation
Preface
-
- Book:
- Nonlinear Continuum Mechanics for Finite Element Analysis
- Published online:
- 06 July 2010
- Print publication:
- 13 March 2008, pp xv-xx
-
- Chapter
- Export citation
5 - STRESS AND EQUILIBRIUM
-
- Book:
- Nonlinear Continuum Mechanics for Finite Element Analysis
- Published online:
- 06 July 2010
- Print publication:
- 13 March 2008, pp 134-154
-
- Chapter
- Export citation
7 - LARGE ELASTO-PLASTIC DEFORMATIONS
-
- Book:
- Nonlinear Continuum Mechanics for Finite Element Analysis
- Published online:
- 06 July 2010
- Print publication:
- 13 March 2008, pp 188-215
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Nonlinear Continuum Mechanics for Finite Element Analysis
- Published online:
- 06 July 2010
- Print publication:
- 13 March 2008, pp i-viii
-
- Chapter
- Export citation