Refine search
Actions for selected content:
8126 results in Fluid dynamics and solid mechanics
Acknowledgments
-
- Book:
- Partial Differential Equations in Fluid Dynamics
- Published online:
- 06 July 2010
- Print publication:
- 28 July 2008, pp xiii-xiv
-
- Chapter
- Export citation
5 - Laplace Transform Methods
-
- Book:
- Partial Differential Equations in Fluid Dynamics
- Published online:
- 06 July 2010
- Print publication:
- 28 July 2008, pp 148-182
-
- Chapter
- Export citation
Contents
-
- Book:
- Partial Differential Equations in Fluid Dynamics
- Published online:
- 06 July 2010
- Print publication:
- 28 July 2008, pp vii-x
-
- Chapter
- Export citation
3 - Eigenvalue Problems and Eigenfunction Expansions
-
- Book:
- Partial Differential Equations in Fluid Dynamics
- Published online:
- 06 July 2010
- Print publication:
- 28 July 2008, pp 62-105
-
- Chapter
- Export citation
7 - Particular Physical Problems
-
- Book:
- Partial Differential Equations in Fluid Dynamics
- Published online:
- 06 July 2010
- Print publication:
- 28 July 2008, pp 217-243
-
- Chapter
- Export citation
1 - Review of Analytic Function Theory
-
- Book:
- Partial Differential Equations in Fluid Dynamics
- Published online:
- 06 July 2010
- Print publication:
- 28 July 2008, pp 1-36
-
- Chapter
- Export citation
6 - Fourier Transform Methods
-
- Book:
- Partial Differential Equations in Fluid Dynamics
- Published online:
- 06 July 2010
- Print publication:
- 28 July 2008, pp 183-216
-
- Chapter
- Export citation
Index
-
- Book:
- Partial Differential Equations in Fluid Dynamics
- Published online:
- 06 July 2010
- Print publication:
- 28 July 2008, pp 279-282
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Partial Differential Equations in Fluid Dynamics
- Published online:
- 06 July 2010
- Print publication:
- 28 July 2008, pp i-vi
-
- Chapter
- Export citation
Preface
-
- Book:
- Partial Differential Equations in Fluid Dynamics
- Published online:
- 06 July 2010
- Print publication:
- 28 July 2008, pp xi-xii
-
- Chapter
- Export citation
4 - Green's Functions for Boundary-Value Problems
-
- Book:
- Partial Differential Equations in Fluid Dynamics
- Published online:
- 06 July 2010
- Print publication:
- 28 July 2008, pp 106-147
-
- Chapter
- Export citation
NEW GRONWALL–OU-IANG TYPE INTEGRAL INEQUALITIES AND THEIR APPLICATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 1 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 111-127
-
- Article
-
- You have access
- Export citation
THE FUNDAMENTAL AND NUMERICAL SOLUTIONS OF THE RIESZ SPACE-FRACTIONAL REACTION–DISPERSION EQUATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 1 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 45-57
-
- Article
-
- You have access
- Export citation
ON THE ORDER OF MAXIMUM ERROR OF THE FINITE DIFFERENCE SOLUTIONS OF LAPLACE’S EQUATION ON RECTANGLES
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 1 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 59-73
-
- Article
-
- You have access
- Export citation
ANOTHER SHARP L2 INEQUALITY OF OSTROWSKI TYPE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 1 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 129-136
-
- Article
-
- You have access
- Export citation
SPACE-LIKE HYPERSURFACES IN LOCALLY SYMMETRIC LORENTZ SPACE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 1 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 1-11
-
- Article
-
- You have access
- Export citation
HYPER-WIENER INDEX OF ZIGZAG POLYHEX NANOTUBES
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 1 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 75-86
-
- Article
-
- You have access
- Export citation
A NOTE ON WITHDRAWAL FROM A TWO-LAYER FLUID THROUGH A LINE SINK IN A POROUS MEDIUM
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 1 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 101-110
-
- Article
-
- You have access
- Export citation
ARITHMETIC MEAN OF VALUES AND VALUE AT MEAN OF ARGUMENTS FOR CONVEX FUNCTIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 1 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 137-141
-
- Article
-
- You have access
- Export citation
STABILITY IN DISTRIBUTION OF NONLINEAR SYSTEMS WITH TIME-VARYING DELAYS AND SEMI-MARKOVIAN SWITCHING
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 1 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 31-44
-
- Article
-
- You have access
- Export citation
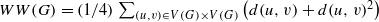 , where
, where 