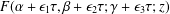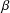Refine search
Actions for selected content:
8126 results in Fluid dynamics and solid mechanics
Index
-
- Book:
- Intermediate Dynamics for Engineers
- Published online:
- 08 February 2020
- Print publication:
- 30 January 2020, pp 522-526
-
- Chapter
- Export citation
4 - Lagrange’s Equations of Motion for a System of Particles
- from Part II - A System of Particles
-
- Book:
- Intermediate Dynamics for Engineers
- Published online:
- 08 February 2020
- Print publication:
- 30 January 2020, pp 137-169
-
- Chapter
- Export citation
ASYMPTOTICS OF A GAUSS HYPERGEOMETRIC FUNCTION WITH TWO LARGE PARAMETERS: A NEW CASE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 62 / Issue 4 / October 2020
- Published online by Cambridge University Press:
- 10 December 2019, pp. 446-452
-
- Article
-
- You have access
- Export citation
NUMERICAL ENTROPY PRODUCTION AS SMOOTHNESS INDICATOR FOR SHALLOW WATER EQUATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 61 / Issue 4 / October 2019
- Published online by Cambridge University Press:
- 28 November 2019, pp. 398-415
-
- Article
-
- You have access
- Export citation
PRICING HOLDER-EXTENDABLE CALL OPTIONS WITH MEAN-REVERTING STOCHASTIC VOLATILITY
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 61 / Issue 4 / October 2019
- Published online by Cambridge University Press:
- 14 October 2019, pp. 382-397
-
- Article
-
- You have access
- Export citation
Multimedia Fluid Mechanics Online
- Site License
-
- Published online:
- 27 September 2019
A MULTIPHASE MULTISCALE MODEL FOR NUTRIENT-LIMITED TISSUE GROWTH, PART II: A SIMPLIFIED DESCRIPTION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 61 / Issue 4 / October 2019
- Published online by Cambridge University Press:
- 18 September 2019, pp. 368-381
-
- Article
-
- You have access
- Export citation
ANZ VOLUME 61 ISSUE 3 COVER AND BACK MATTER
-
- Journal:
- The ANZIAM Journal / Volume 61 / Issue 3 / July 2019
- Published online by Cambridge University Press:
- 02 September 2019, pp. b1-b6
-
- Article
-
- You have access
- Export citation
ANZ VOLUME 61 ISSUE 3 COVER AND FRONT MATTER
-
- Journal:
- The ANZIAM Journal / Volume 61 / Issue 3 / July 2019
- Published online by Cambridge University Press:
- 02 September 2019, pp. f1-f2
-
- Article
-
- You have access
- Export citation

The Seismic Wavefield
-
- Published online:
- 31 August 2019
- Print publication:
- 23 December 2002
Contents
-
- Book:
- Chemical Kinetics in Combustion and Reactive Flows
- Published online:
- 16 August 2019
- Print publication:
- 22 August 2019, pp ix-xii
-
- Chapter
- Export citation
3 - Software Tools for the Support of Calculation of Combustion and Reacting Flows
- from Part I - Basic Components of Chemical Nonequilibrium Models
-
- Book:
- Chemical Kinetics in Combustion and Reactive Flows
- Published online:
- 16 August 2019
- Print publication:
- 22 August 2019, pp 95-204
-
- Chapter
- Export citation
Part III - Simulation of Combustion and Nonequilibrium Flows in Propulsion and Power Generation Systems
-
- Book:
- Chemical Kinetics in Combustion and Reactive Flows
- Published online:
- 16 August 2019
- Print publication:
- 22 August 2019, pp 281-396
-
- Chapter
- Export citation
Part II - Mathematical Modeling of Selected Typical Modes of Combustion
-
- Book:
- Chemical Kinetics in Combustion and Reactive Flows
- Published online:
- 16 August 2019
- Print publication:
- 22 August 2019, pp 205-280
-
- Chapter
- Export citation
Acknowledgments
-
- Book:
- Chemical Kinetics in Combustion and Reactive Flows
- Published online:
- 16 August 2019
- Print publication:
- 22 August 2019, pp xix-xx
-
- Chapter
- Export citation
Index
-
- Book:
- Chemical Kinetics in Combustion and Reactive Flows
- Published online:
- 16 August 2019
- Print publication:
- 22 August 2019, pp 418-422
-
- Chapter
- Export citation
Preface
-
- Book:
- Chemical Kinetics in Combustion and Reactive Flows
- Published online:
- 16 August 2019
- Print publication:
- 22 August 2019, pp xiii-xviii
-
- Chapter
- Export citation
1 - Approaches to Combustion Simulation
- from Part I - Basic Components of Chemical Nonequilibrium Models
-
- Book:
- Chemical Kinetics in Combustion and Reactive Flows
- Published online:
- 16 August 2019
- Print publication:
- 22 August 2019, pp 3-40
-
- Chapter
- Export citation
4 - Laminar Premixed Flames: Simulation of Combustion in the Flame Front
- from Part II - Mathematical Modeling of Selected Typical Modes of Combustion
-
- Book:
- Chemical Kinetics in Combustion and Reactive Flows
- Published online:
- 16 August 2019
- Print publication:
- 22 August 2019, pp 207-227
-
- Chapter
- Export citation
5 - Droplets and Particles: Evaporation in High-Temperature Flow and Combustion in Boundary Layers
- from Part II - Mathematical Modeling of Selected Typical Modes of Combustion
-
- Book:
- Chemical Kinetics in Combustion and Reactive Flows
- Published online:
- 16 August 2019
- Print publication:
- 22 August 2019, pp 228-261
-
- Chapter
- Export citation