Skip to main content Accessibility help
×
  1. Home
  2. Browse subjects
  3. Mathematics
  4. Fluid dynamics and solid mechanics
  5. Content listing

Refine search

Refine search

Access:
Content type:
Publication date:
Apply   From and To filters
Subject: Show more
Journals Show more
Publishers: Show more
Societies Show more
Series: Show more
Collections: Show more

Actions for selected content:

Select all | Deselect all
  • View selected items
  • Export citations
  • Download PDF (zip)
  • Save to Kindle
  • Save to Dropbox
  • Save to Google Drive

Save Search

You can save your searches here and later view and run them again in "My saved searches".

Please provide a title, maximum of 40 characters.
Cancel
×

8124 results in Fluid dynamics and solid mechanics

Page 88 of 407

  • ANZ VOLUME 60 ISSUE 1 COVER AND FRONT MATTER

  • Journal:
    The ANZIAM Journal / Volume 60 / Issue 1 / July 2018
    Published online by Cambridge University Press:
    13 September 2018, pp. f1-f2
    • Article
      • You have access
    • PDF
    • Export citation

  • OPTION PRICING UNDER THE KOBOL MODEL

  • Part of
  • WENTING CHEN, SHA LIN
  • Journal:
    The ANZIAM Journal / Volume 60 / Issue 2 / October 2018
    Published online by Cambridge University Press:
    12 September 2018, pp. 175-190
    • Article
      • You have access
    • PDF
    • Export citation

  • We consider the pricing of European options under a modified Black–Scholes equation having fractional derivatives in the “spatial” (price) variable. To be specific, the underlying price is assumed to follow a geometric Koponen–Boyarchenko–Levendorski process. This pure jump Lévy process could better capture the real behaviour of market data. Despite many difficulties caused by the “globalness” of the fractional derivatives, we derive an explicit closed-form analytical solution by solving the fractional partial differential equation analytically, using the Fourier transform technique. Based on the newly derived formula, we also examine, in theory, many basic properties of the option price under the current model. On the other hand, for practical purposes, we impose a reliable implementation method for the current formula so that it can be easily used in the trading market. With the numerical results, the impact of different parameters on the option price are also investigated.

  • EFFECT OF UNIFORM WIND FLOW ON MODULATIONAL INSTABILITY OF TWO CROSSING WAVES OVER FINITE DEPTH WATER

  • Part of
  • SUMANA KUNDU, SUMA DEBSARMA, K. P. DAS
  • Journal:
    The ANZIAM Journal / Volume 60 / Issue 1 / July 2018
    Published online by Cambridge University Press:
    31 August 2018, pp. 118-136
    • Article
      • You have access
    • PDF
    • Export citation

  • The effect of uniform wind flow on modulational instability of two crossing waves is studied here. This is an extension of an earlier work to the case of a finite-depth water body. Evolution equations are obtained as a set of three coupled nonlinear equations correct up to third order in wave steepness. Figures presented in this paper display the variation in the growth rate of instability of a pair of obliquely interacting uniform wave trains with respect to the changes in the air-flow velocity, depth of water medium and the angle between the directions of propagation of the two wave packets. We observe that the growth rate of instability increases with the increase in the wind velocity and the depth of water medium. It also increases with the decrease in the angle of interaction of the two wave systems.

  • ON THE 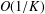$O(1/K)$ CONVERGENCE RATE OF THE ALTERNATING DIRECTION METHOD OF MULTIPLIERS IN A COMPLEX DOMAIN

  • Part of
  • L. LI, G. Q. WANG, J. L. ZHANG
  • Journal:
    The ANZIAM Journal / Volume 60 / Issue 1 / July 2018
    Published online by Cambridge University Press:
    30 August 2018, pp. 95-117
    • Article
      • You have access
    • PDF
    • Export citation

  • We focus on the convergence rate of the alternating direction method of multipliers (ADMM) in a complex domain. First, the complex form of variational inequality (VI) is established by using the Wirtinger calculus technique. Second, the $O(1/K)$ convergence rate of the ADMM in a complex domain is provided. Third, the ADMM in a complex domain is applied to the least absolute shrinkage and selectionator operator (LASSO). Finally, numerical simulations are provided to show that ADMM in a complex domain has the $O(1/K)$ convergence rate and that it has certain advantages compared with the ADMM in a real domain.

Microhydrodynamics, Brownian Motion, and Complex Fluids
  • Michael D. Graham
  • Published online:
    27 August 2018
    Print publication:
    13 September 2018
  • This is an introduction to the dynamics of fluids at small scales, the physical and mathematical underpinnings of Brownian motion, and the application of these subjects to the dynamics and flow of complex fluids such as colloidal suspensions and polymer solutions. It brings together continuum mechanics, statistical mechanics, polymer and colloid science, and various branches of applied mathematics, in a self-contained and integrated treatment that provides a foundation for understanding complex fluids, with a strong emphasis on fluid dynamics. Students and researchers will find that this book is extensively cross-referenced to illustrate connections between different aspects of the field. Its focus on fundamental principles and theoretical approaches provides the necessary groundwork for research in the dynamics of flowing complex fluids.

Page 88 of 407