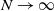Refine listing
Actions for selected content:
26 results in 93Cxx
REDUCING ENERGY DURING SPECIFIED TIME INTERVALS FOR MULTIPLE TRAINS USING SIMPLE TRAIN MODELS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 26 August 2025, e30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal control of a reaction-diffusion epidemic model with non-compliance
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 14 April 2025, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Exponential turnpike property for particle systems and mean-field limit
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 27 January 2025, pp. 993-1011
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The turnpike property for mean-field optimal control problems
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 12 February 2024, pp. 733-747
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stabilization of the Kawahara–Kadomtsev–Petviashvili equation with time-delayed feedback
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 11 September 2023, pp. 280-306
- Print publication:
- February 2025
-
- Article
- Export citation
Characterization of the optimal average cost in Markov decision chains driven by a risk-seeking controller
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 21 July 2023, pp. 340-367
- Print publication:
- March 2024
-
- Article
- Export citation
Constrained exact boundary controllability of a semilinear model for pipeline gas flow
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 01 February 2023, pp. 532-553
-
- Article
- Export citation
On a mixed singular/switching control problem with multiple regimes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 22 August 2022, pp. 743-782
- Print publication:
- September 2022
-
- Article
- Export citation
Resilient tracking consensus over dynamic random graphs: A linear system approach
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 12 July 2022, pp. 408-423
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MODEL-BASED ADAPTIVE MONITORING: IMPROVING THE EFFECTIVENESS OF REEF MONITORING PROGRAMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 09 February 2022, pp. 511-513
- Print publication:
- June 2022
-
- Article
-
- You have access
- HTML
- Export citation
EVOLUTIONARY DYNAMICS IN DISCRETE TIME FOR THE PERTURBED POSITIVE DEFINITE REPLICATOR EQUATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 62 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 09 December 2020, pp. 148-184
-
- Article
-
- You have access
- Export citation
Controllability of stochastic nonlinear oscillating delay systems driven by the Rosenblatt distribution
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 03 March 2020, pp. 217-239
- Print publication:
- February 2021
-
- Article
- Export citation
A SEPARATION PRINCIPLE FOR THE STABILISATION OF A CLASS OF FRACTIONAL ORDER TIME DELAY NONLINEAR SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 30 August 2018, pp. 161-173
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
ON THE
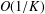 $O(1/K)$ CONVERGENCE RATE OF THE ALTERNATING DIRECTION METHOD OF MULTIPLIERS IN A COMPLEX DOMAIN
$O(1/K)$ CONVERGENCE RATE OF THE ALTERNATING DIRECTION METHOD OF MULTIPLIERS IN A COMPLEX DOMAIN
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 60 / Issue 1 / July 2018
- Published online by Cambridge University Press:
- 30 August 2018, pp. 95-117
-
- Article
-
- You have access
- Export citation
GLOBAL A PRIORI IDENTIFIABILITY OF MODELS OF FLOW-CELL OPTICAL BIOSENSOR EXPERIMENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 14 June 2018, pp. 350-352
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
Analysis of Mathematics and Numerical Pattern Formation in Superdiffusive Fractional Multicomponent System
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 6 / December 2017
- Published online by Cambridge University Press:
- 28 November 2017, pp. 1438-1460
- Print publication:
- December 2017
-
- Article
- Export citation
PINNING SYNCHRONIZATION OF FRACTIONAL-ORDER COMPLEX NETWORKS BY A SINGLE CONTROLLER
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 324-332
-
- Article
-
- You have access
- Export citation
POSITIVE ALMOST PERIODIC SOLUTIONS FOR THE HEMATOPOIESIS MODEL VIA THE HILBERT PROJECTIVE METRIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 19 October 2016, pp. 84-93
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
A Computational Study of a Data Assimilation Algorithm for the Two-dimensional Navier-Stokes Equations
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 12 April 2016, pp. 1094-1110
- Print publication:
- April 2016
-
- Article
- Export citation
Differential Equations Driven by Π-Rough Paths
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 21 January 2016, pp. 741-758
-
- Article
- Export citation