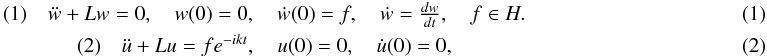Refine search
Actions for selected content:
6997 results in Mathematical modeling and methods
Inverse Scattering Problem for the Maxwell’sEquations
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 8 / Issue 1 / 2013
- Published online by Cambridge University Press:
- 28 January 2013, pp. 200-206
- Print publication:
- 2013
-
- Article
- Export citation
Entire Solutions in Lattice Delayed Differential Equations withNonlocal Interaction: Bistable Cases
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 8 / Issue 3 / 2013
- Published online by Cambridge University Press:
- 12 June 2013, pp. 78-103
- Print publication:
- 2013
-
- Article
- Export citation
The Dynamical Impact of a Shortcut in Unidirectionally CoupledRings of Oscillators
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 8 / Issue 5 / 2013
- Published online by Cambridge University Press:
- 17 September 2013, pp. 173-189
- Print publication:
- 2013
-
- Article
- Export citation
Wave Trains Associated with a Cascade of Bifurcations ofSpace-Time Caustics over Elongated Underwater Banks
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 8 / Issue 5 / 2013
- Published online by Cambridge University Press:
- 17 September 2013, pp. 1-12
- Print publication:
- 2013
-
- Article
- Export citation
Spectral Properties of Schrödinger-type Operators andLarge-time Behavior of the Solutions to the Corresponding Wave Equation
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 8 / Issue 1 / 2013
- Published online by Cambridge University Press:
- 28 January 2013, pp. 207-214
- Print publication:
- 2013
-
- Article
- Export citation
Inside Dynamics of Delayed Traveling Waves
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 8 / Issue 3 / 2013
- Published online by Cambridge University Press:
- 12 June 2013, pp. 42-59
- Print publication:
- 2013
-
- Article
- Export citation
The Construction of Smooth Parseval Frames ofShearlets
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 8 / Issue 1 / 2013
- Published online by Cambridge University Press:
- 28 January 2013, pp. 82-105
- Print publication:
- 2013
-
- Article
- Export citation
Mathematical Modelling Plant SignallingNetworks
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 8 / Issue 4 / 2013
- Published online by Cambridge University Press:
- 10 July 2013, pp. 5-24
- Print publication:
- 2013
-
- Article
- Export citation
Heat Transfer in a Medium in Which Many Small Particles AreEmbedded
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 8 / Issue 1 / 2013
- Published online by Cambridge University Press:
- 28 January 2013, pp. 193-199
- Print publication:
- 2013
-
- Article
- Export citation
Semiclassical Limits of Heat Kernels of Laplacians on theh-Heisenberg Group
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 8 / Issue 1 / 2013
- Published online by Cambridge University Press:
- 28 January 2013, pp. 132-142
- Print publication:
- 2013
-
- Article
- Export citation
Instabilities and Dynamics of Weakly SubcriticalPatterns
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 8 / Issue 5 / 2013
- Published online by Cambridge University Press:
- 17 September 2013, pp. 131-154
- Print publication:
- 2013
-
- Article
- Export citation
Preface
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 8 / Issue 4 / 2013
- Published online by Cambridge University Press:
- 10 July 2013, pp. 1-4
- Print publication:
- 2013
-
- Article
-
- You have access
- Export citation
A Remark on the Hull of a Multi-Dimensional Limit-PeriodicPotential
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 8 / Issue 1 / 2013
- Published online by Cambridge University Press:
- 28 January 2013, pp. 75-81
- Print publication:
- 2013
-
- Article
- Export citation
Nonlinear Whirlpools Versus Harmonic Waves in a Rotating Columnof Stratified Fluid
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 8 / Issue 1 / 2013
- Published online by Cambridge University Press:
- 28 January 2013, pp. 122-131
- Print publication:
- 2013
-
- Article
- Export citation
Identifiability for Linearized Sine-GordonEquation
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 8 / Issue 1 / 2013
- Published online by Cambridge University Press:
- 28 January 2013, pp. 106-121
- Print publication:
- 2013
-
- Article
- Export citation
Existence and Stability of Travelling Front Solutions forGeneral Auto-catalytic Chemical Reaction Systems
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 8 / Issue 3 / 2013
- Published online by Cambridge University Press:
- 12 June 2013, pp. 104-132
- Print publication:
- 2013
-
- Article
- Export citation
Mathematical Models for Expansive Growth of Cells withWalls
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 8 / Issue 4 / 2013
- Published online by Cambridge University Press:
- 10 July 2013, pp. 35-61
- Print publication:
- 2013
-
- Article
- Export citation
Properties of Discrete Framelet Transforms
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 8 / Issue 1 / 2013
- Published online by Cambridge University Press:
- 28 January 2013, pp. 18-47
- Print publication:
- 2013
-
- Article
- Export citation
Spatial Demogenetic Model for Studying Phenomena Observed uponIntroduction of the Ragweed Leaf Beetle in the South of Russia
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 8 / Issue 6 / 2013
- Published online by Cambridge University Press:
- 28 November 2013, pp. 80-95
- Print publication:
- 2013
-
- Article
- Export citation
Application of Fractional Differential Equations in Modellingthe Subdiffusion–Reaction Process
-
- Journal:
- Mathematical Modelling of Natural Phenomena / Volume 8 / Issue 2 / 2013
- Published online by Cambridge University Press:
- 24 April 2013, pp. 44-54
- Print publication:
- 2013
-
- Article
- Export citation