Refine listing
Actions for selected content:
25 results in 14Rxx
K1(
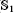 ) and the group of automorphisms of the algebra
) and the group of automorphisms of the algebra 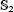 of one-sided inverses of a polynomial algebra in two variables
of one-sided inverses of a polynomial algebra in two variables
- Part of
-
- Journal:
- Journal of K-Theory / Volume 10 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 24 May 2012, pp. 583-601
- Print publication:
- December 2012
-
- Article
- Export citation
Invariants of hyperplane groups and vanishing ideals of finite sets of points
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 16 March 2012, pp. 355-367
-
- Article
-
- You have access
- Export citation
POLYNOMIAL ENDOMORPHISMS PRESERVING OUTER RANK IN TWO VARIABLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 2 / October 2012
- Published online by Cambridge University Press:
- 16 February 2012, pp. 186-192
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
Corrigendum: ‘A new proof of the non-tameness of the Nagata automorphism from the point of view of the Sarkisov Program, Compositio Math. 144 (2008), 963–977’
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 4 / July 2010
- Published online by Cambridge University Press:
- 16 June 2010, pp. 999-1001
- Print publication:
- July 2010
-
- Article
-
- You have access
- Export citation
A new proof of the non-tameness of the Nagata automorphism from the point of view of the Sarkisov program
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 4 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 963-977
- Print publication:
- July 2008
-
- Article
-
- You have access
- Export citation
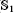 ) and the group of automorphisms of the algebra
) and the group of automorphisms of the algebra 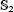 of one-sided inverses of a polynomial algebra in two variables
of one-sided inverses of a polynomial algebra in two variables

 is the 2-dimensional algebraic torus,
is the 2-dimensional algebraic torus, 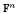 , the vanishing ideal of
, the vanishing ideal of 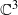 . For a long time, it remained unknown whether or not the Nagata automorphism is tame until Shestakov and Umirbaev at last proved that it is not tame in 2004, by purely algebraic methods (e.g. Poisson algebra). In this paper, we consider a certain necessary condition for a given automorphism on
. For a long time, it remained unknown whether or not the Nagata automorphism is tame until Shestakov and Umirbaev at last proved that it is not tame in 2004, by purely algebraic methods (e.g. Poisson algebra). In this paper, we consider a certain necessary condition for a given automorphism on 