Refine listing
Actions for selected content:
92 results in 55Nxx
COHOMOLOGY OF THE PINWHEEL TILING
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 27 August 2014, pp. 162-179
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
The elliptic Weyl character formula
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 7 / July 2014
- Published online by Cambridge University Press:
- 12 May 2014, pp. 1196-1234
- Print publication:
- July 2014
-
- Article
- Export citation
A generalization of Ohkawa’s theorem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 5 / May 2014
- Published online by Cambridge University Press:
- 03 April 2014, pp. 893-902
- Print publication:
- May 2014
-
- Article
- Export citation
The tangent complex and Hochschild cohomology of
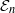 $\mathcal {E}_n$-rings
$\mathcal {E}_n$-rings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 3 / March 2013
- Published online by Cambridge University Press:
- 10 December 2012, pp. 430-480
- Print publication:
- March 2013
-
- Article
- Export citation
Spaces with Noetherian cohomology
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 05 December 2012, pp. 13-25
-
- Article
-
- You have access
- Export citation
GEOMETRIC AND TOPOLOGICAL STRUCTURES RELATED TO M-BRANES II: TWISTED STRING AND STRINGC STRUCTURES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 09 June 2011, pp. 93-108
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation
Uniqueness of Morava K-theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 2 / March 2011
- Published online by Cambridge University Press:
- 27 September 2010, pp. 633-648
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
Equivariant KK-theory for inverse limits of G-C*-algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 2 / April 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 183-211
- Print publication:
- April 1994
-
- Article
-
- You have access
- Export citation
Twistor diagrams and the algebraic de Rham theorem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 54 / Issue 2 / April 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 221-235
- Print publication:
- April 1993
-
- Article
-
- You have access
- Export citation
Cohomology with exotic supports and the generalized excision
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 45 / Issue 3 / December 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 326-340
- Print publication:
- December 1988
-
- Article
-
- You have access
- Export citation
Continuous trace C*-algebras with given Dixmer-Douady class
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 3 / June 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 394-407
- Print publication:
- June 1985
-
- Article
-
- You have access
- Export citation
On large cohomological dimension and tautness
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 3 / December 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 391-404
- Print publication:
- December 1984
-
- Article
-
- You have access
- Export citation
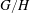
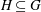
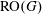
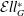
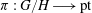
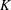
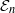
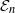
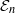
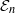
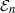
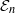
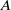
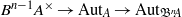
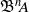
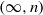
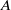
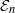
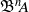
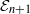
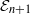
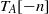
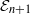
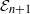
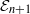
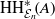

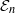
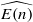 -algebra structures. Here
-algebra structures. Here 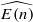 is the
is the 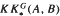 are extended to the setting of inverse limits of
are extended to the setting of inverse limits of 