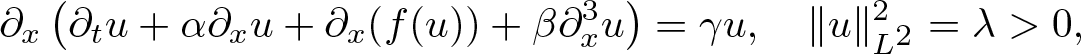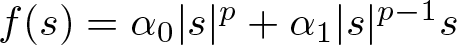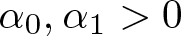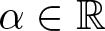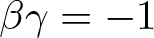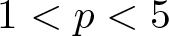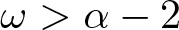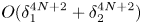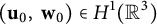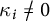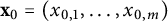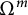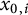Refine listing
Actions for selected content:
66 results in 76Bxx
Pensive Billiards, Point Vortices, And The Silver Ratio
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 13 October 2025, e171
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
WAVE INTERACTION WITH AN H-SHAPED SUBMERGED BREAKWATER
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 15 September 2025, e32
-
- Article
- Export citation
NONLINEAR MODULATION OF RANDOM WAVE SPECTRA FOR SURFACE-GRAVITY WAVES WITH LINEAR SHEAR CURRENTS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 66 / Issue 4 / October 2024
- Published online by Cambridge University Press:
- 10 January 2025, pp. 222-237
-
- Article
- Export citation
HARMONIC RESONANCE OF SHORT-CRESTED GRAVITY WAVES ON DEEP WATER: ON THEIR PERSISTENCY
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 67 / 2025
- Published online by Cambridge University Press:
- 03 December 2024, e1
-
- Article
- Export citation
Spectral stability of constrained solitary waves for a generalized Ostrovsky equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 November 2024, pp. 1-32
-
- Article
- Export citation
Wake flow past a submerged plate near a free surface
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 25 October 2024, pp. 524-537
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
IRROTATIONAL FLOW DUE TO FORCED OSCILLATIONS OF A BUBBLE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 66 / Issue 3 / July 2024
- Published online by Cambridge University Press:
- 18 October 2024, pp. 152-180
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the reconstruction of unknown driving forces from low-mode observations in the 2D Navier–Stokes equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 01 April 2024, pp. 1-24
-
- Article
- Export citation
A mathematical analysis of the Kakinuma model for interfacial gravity waves. Part II: justification as a shallow water approximation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 March 2024, pp. 1-72
-
- Article
- Export citation
EXTRACTION OF DENSITY-LAYERED FLUID FROM A POROUS MEDIUM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 07 March 2024, pp. 594-595
- Print publication:
- June 2024
-
- Article
-
- You have access
- HTML
- Export citation
NONLINEAR SELF-MODULATION OF GRAVITY-CAPILLARY WAVES ON SHEAR CURRENTS IN FINITE DEPTH
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 65 / Issue 3 / July 2023
- Published online by Cambridge University Press:
- 12 January 2024, pp. 248-272
-
- Article
- Export citation
MODELS OF FLOW AND DIFFUSION: SELECTIVE WITHDRAWAL FROM A STRATIFIED FLUID AND DISPERSAL OF HYDROGEN IN THE RETINA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 04 April 2023, pp. 520-521
- Print publication:
- June 2023
-
- Article
-
- You have access
- HTML
- Export citation
A MODIFICATION TO THE SCHRÖDINGER EQUATION FOR BROADER BANDWIDTH GRAVITY-CAPILLARY WAVES ON DEEP WATER WITH DEPTH-UNIFORM CURRENT
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 64 / Issue 3 / July 2022
- Published online by Cambridge University Press:
- 03 March 2023, pp. 292-313
-
- Article
- Export citation
Global existence of the strong solution to the 3D incompressible micropolar equations with fractional partial dissipation
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 13 September 2022, pp. 1516-1539
- Print publication:
- October 2023
-
- Article
- Export citation
Existence of stationary vortex sheets for the 2D incompressible Euler equation
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 05 May 2022, pp. 828-853
- Print publication:
- June 2023
-
- Article
- Export citation
A DYNAMICAL STUDY OF SALINE PLUMES IN DESALINATION OUTFALLS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 01 March 2022, pp. 523-524
- Print publication:
- June 2022
-
- Article
-
- You have access
- HTML
- Export citation
A spectral modelling approach for fluid flow into a line sink in a confined aquifer
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 01 November 2021, pp. 960-981
-
- Article
- Export citation
IDEAL PLANAR FLUID FLOW OVER A SUBMERGED OBSTACLE: REVIEW AND EXTENSION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 63 / Issue 4 / October 2021
- Published online by Cambridge University Press:
- 25 October 2021, pp. 377-419
-
- Article
- Export citation
Concentrating standing waves for Davey–Stewartson systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 01 October 2021, pp. 1411-1450
- Print publication:
- December 2022
-
- Article
- Export citation
Global regularity for the micropolar Rayleigh-Bénard problem with only velocity dissipation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 26 August 2021, pp. 1109-1138
- Print publication:
- October 2022
-
- Article
- Export citation