In this article we show that the Czech mathematician Václav Šimerka discovered the factorization of $\frac{1}{9} (1{0}^{17} - 1)$ using a method based on the class group of binary quadratic forms more than 120 years before Shanks and Schnorr developed similar algorithms. Šimerka also gave the first examples of what later became known as Carmichael numbers.

Probability theory, and its dynamic aspect stochastic process theory, is both a venerable subject, in that its roots go back to the mid-seventeenth century, and a young one, in that its modern formulation happened comparatively recently - well within living memory. The year 2003 marked the seventieth anniversary of Kolmogorov's Grundbegriffe der Wahrscheinlichkeitsrechnung, usually regarded as having inaugurated modern (measure-theoretic) probability theory. It also marked the fiftieth anniversary of Doob's Stochastic Processes. The profound and continuing influence of this classic work prompts the present piece.

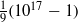
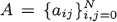The paper characterizes matrices which have a given system of vectors orthogonal with respect to a given probability distribution as its right eigenvectors. Results of Hoare and Rahman are unified in this context, then all matrices with a given orthogonal polynomial system as right eigenvectors under the constraint a0j = 0 for j ≥ 2 are specified. The only stochastic matrices P = {pij} satisfying p00 + p01 = 1 with the Hahn polynomials as right eigenvectors have the form of the Moran mutation model.

David Vere-Jones's interest in mathematical and statistical education was triggered in the early 1960s during his visits to Russia when he met leading mathematicians who were deeply involved in these areas as well as in their own research. Through the 1970s and 1980s David's involvement in education grew in New Zealand where he became influential in the developments in mathematics and statistics teaching, especially at school level. By the early 1990s he had become very involved in the Education Committee of the International Statistical Institute (ISI) and had a key role in the Third International Conference on Teaching Statistics (ICOTS-3) in Dunedin, 1990. This was soon followed by the pivotal role he played in the establishment of the International Association for Statistical Education (IASE). This paper describes the formative influences underlying David's involvement in statistical education and his influence on the growth of the IASE.

This is an expanded version of two lectures given at the conference held at Sydney University in December 1997 on the 50th anniversary of the death of G. H. Hardy.