We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
By methods of harmonic analysis, we identify large classes of Banach spaces invariant of periodic Fourier multipliers with symbols satisfying the classical Marcinkiewicz type conditions. Such classes include general (vector-valued) Banach function spaces Φ and/or the scales of Besov and Triebel–Lizorkin spaces defined on the basis of Φ.
We apply these results to the study of the well-posedness and maximal regularity property of an abstract second-order integro-differential equation, which models various types of elliptic and parabolic problems arising in different areas of applied mathematics. In particular, under suitable conditions imposed on a convolutor c and the geometry of an underlying Banach space X, we characterize the conditions on the operators A, B, and P on X such that the following periodic problem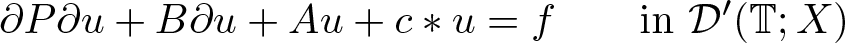
\begin{equation*}\partial P \partial u + B \partial u + {A} u + c \ast u = f \qquad \textrm{in } {\mathcal D}'({\mathbb{T}}; X)\end{equation*}
is well-posed with respect to large classes of function spaces. The obtained results extend the known theory on the maximal regularity of such problem.
