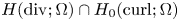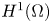Refine listing
Actions for selected content:
17 results in 74Axx
A global higher regularity result for the static relaxed micromorphic model on smooth domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 20 May 2024, pp. 1-15
-
- Article
- Export citation
Breakdown of electroneutrality in polyelectrolyte gels
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 35 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 06 September 2023, pp. 359-381
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
WALL STABILIZATION IN MINES BY SPRAY-ON LINERS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 65 / Issue 1-2 / January 2023
- Published online by Cambridge University Press:
- 31 August 2023, pp. 55-78
-
- Article
- Export citation
 $n$-coupling mechanisms are sufficient to obtain exponential decay in strain gradient elasticity
$n$-coupling mechanisms are sufficient to obtain exponential decay in strain gradient elasticity
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 22 May 2023, pp. 1288-1298
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Modelling, computation and analysis on combustion of explosives
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 05 February 2021, pp. 27-57
-
- Article
- Export citation
THE MAGNETIC FIELD ABOUT A THREE-DIMENSIONAL BLOCK NEODYMIUM MAGNET
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 62 / Issue 4 / October 2020
- Published online by Cambridge University Press:
- 22 June 2020, pp. 386-405
-
- Article
-
- You have access
- Export citation
Multiscale modelling and homogenisation of fibre-reinforced hydrogels for tissue engineering
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 22 November 2018, pp. 143-171
-
- Article
-
- You have access
- Export citation
A Unified Momentum Equation Approach for Computing Flow-Induced Stresses in Structures with Arbitrarily-Shaped Stationary Boundaries
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 1 / July 2017
- Published online by Cambridge University Press:
- 03 May 2017, pp. 39-63
- Print publication:
- July 2017
-
- Article
- Export citation
XFEM for Fracture Analysis in 2D Anisotropic Elasticity
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 11 October 2016, pp. 125-143
- Print publication:
- February 2017
-
- Article
- Export citation
Similarity Solution for the Synchronous Grouting of Shield Tunnel Under the Vertical Non-Axisymmetric Displacement Boundary Condition
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 11 October 2016, pp. 205-232
- Print publication:
- February 2017
-
- Article
- Export citation
A Mixed Analytical/Numerical Method for Velocity and Heat Transfer of Laminar Power-Law Fluids
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 9 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 20 July 2016, pp. 315-336
- Print publication:
- August 2016
-
- Article
- Export citation
DIRECT EXPRESSION OF INCOMPATIBILITY IN CURVILINEAR SYSTEMS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 1 / July 2016
- Published online by Cambridge University Press:
- 08 July 2016, pp. 33-50
-
- Article
-
- You have access
- Export citation
Brittle and Ductile Character of Amorphous Solids
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 27 January 2016, pp. 485-498
- Print publication:
- June 2016
-
- Article
- Export citation
A Numerical Scheme for Generalized Peierls-Nabarro Model of Dislocations Based on the Fast Multipole Method and Iterative Grid Redistribution
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 5 / November 2015
- Published online by Cambridge University Press:
- 23 November 2015, pp. 1282-1312
- Print publication:
- November 2015
-
- Article
- Export citation
PREDICTION OF FLUID SLIP AT GRAPHENE AND CARBON NANOTUBE INTERFACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 05 February 2014, pp. 171-172
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
A CONCEPTUAL MODEL FOR THE ORIGINS OF GEOTHERMAL AND VOLCANIC ACTIVITY IN THE NORTH ISLAND OF NEW ZEALAND
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 3 / January 2009
- Published online by Cambridge University Press:
- 03 November 2009, pp. 421-425
-
- Article
-
- You have access
- Export citation
A MATHEMATICAL MODEL FOR THE LARGE-SCALE TRANSPORT OF HEAT AND WATER IN THE TAUPO VOLCANIC ZONE OF NEW ZEALAND
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 3 / January 2009
- Published online by Cambridge University Press:
- 03 November 2009, pp. 343-354
-
- Article
-
- You have access
- Export citation