The object of this note is to show that the equation of the quadric in n dimensions can be transformed to a ‘focus-directrix’ form which is exactly similar to those for two and three dimensions: this form is extended throughout by the introduction of a constant k. A short discussion of confocal quadrics is appended.

The paper considers the application of Dirac's classical theory of radiating electrons to consider the straight line motion of an electron towards a fixed proton and the straight line motion of two oppositely charged electrons. The paper also gives a discussion of the probable solutions in two- and three-dimensional motions of an electron moving round a fixed proton. In all these cases there appears to be no solution which would permit a collision between the two particles.

I take this opportunity to express my deepest gratitude to Prof. Dirac for his patient guidance and supervision, and also to Christ's College for a scholarship.

Note added. In the problem of the rectilinear motion considered in section (2), if we take the charges on the particles to be of like signs, then we find that the equations of motion have a solution which corresponds to a collision. In place of equation (4) we have

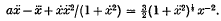
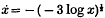It can be easily verified that under suitable initial conditions there is a solution with x→0 and y→∞. Near x=0 the solution is approximately . Thus a collision is possible for like charges and not possible for unlike charges. The result, in both cases, is the opposite of what we should expect from elementary physical considerations.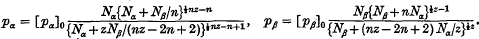

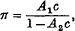
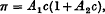
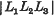
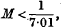
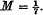The problem of the energy loss by radiation of an electron in a Coulomb field has been solved, using relativistic equations and the Born approximation, by Bethe and Heitler, and, using exact non-relativistic equations, by Sommerfeld; the first of these solutions is valid only for relatively high and the second for relatively low energies. In this paper an exact solution of the problem is given using the relativistic Coulomb wave functions, but depending on a final stage of numerical computation. The method is an extension of that used to determine cross-sections for pair production.

The purpose of this paper is the determination as accurately as possible of the equation of state for the simplest stable crystal, the cubic face-centred lattice, and the comparison of the result with those obtained by rough approximations(1) in order to get an estimate of the reliability of the latter if applied to more involved problems where exact calculations are impossible.

If a particle counter is subject to the radiation from a pure radioactive source of sensibly constant activity, it is axiomatic to suppose that the series of events constituted of the traversals of the counter by ionizing particles is a random series in relation to distribution in time. There are various reasons why the related series of events formed by the occasions on which the counter responds to these ionizing particles is not a random one—and there may also be cases in which the primary source does not, in fact, give rise to particles traversing the counter in a random sequence. The counter responses will necessarily depart from strict randomness in time because of the finite recovery time of the counter; they may also depart from strict randomness through a not uncommon counter defect, the occurrence of ‘spurious’ discharges correlated in some way with the ‘true’ discharges brought about as a result of the ionization produced by the particles. On the other hand, the original ionizing events will not have the effect of a random sequence, even with a pure radioactive source, if secondary radiations are emitted—even in a fraction of the disintegrations—with a time delay appreciable in relation to the counter resolving time, and, clearly, they may depart considerably from true randomness in time if the source is not a pure source, and, in particular, if there is produced in the source material a ‘daughter’ radioelement of lifetime comparable with this resolving time, or with the mean time between counter discharges.

A number of errors have unfortunately been made in the last section of the above paper.

(1) ‘log’ should be deleted from equation (44).

(2) The simplification of equation (45) which was presented neglects some important terms, with the result that the later equations give only the limiting values of osmotic pressure and vapour pressure at infinite dilution. The section following equation (45) must therefore be ignored.

The suffixes used in logic to indicate differences of type may be regarded either as belonging to the formalism itself, or as being part of the machinery for deciding which rows of symbols (without suffixes) are to be admitted as significant. The two different attitudes do not necessarily lead to different formalisms, but when types are regarded as only one way of regulating the calculus it is natural to consider other possible ways, in particular the direct characterization of the significant formulae. Direct criteria for stratification were given by Quine, in his ‘New Foundations for Mathematical Logic’ (7). In the corresponding typed form of this theory ordinary integers are adequate as type-suffixes, and the direct description is correspondingly simple, but in other theories, including that recently proposed by Church(4), a partially ordered set of types must be used. In the present paper criteria, equivalent to the existence of a correct typing, are given for a general class of formalisms, which includes Church's system, several systems proposed by Quine, and (with some slight modifications, given in the last paragraph) Principia Mathematica. (The discussion has been given this general form rather with a view to clarity than to comprehensiveness.)

In 1939 I published a paper in the American Journal of Chemical Physics (Born(1)) in which I tried to develop the thermodynamics of a crystal lattice in the domain of classical (Boltzmann) statistics. Definite formulae and numerical tables for the temperature dependence of the elastic constants up to the melting point were obtained; nevertheless the work was unsatisfactory not only because the approximations used were rough and their accuracy not known, but because a fundamental difficulty with respect to lattice stability turned up. This led to a series of investigations by my collaborators and myself, published in these Proceedings under the title ‘On the stability of crystal lattices’ (quoted here as S I to SIX), by which the difficulty mentioned has been removed. It is now possible to return to the original problem, to which the present series of papers is devoted. In this introduction I wish to recapitulate the whole situation and to explain the plan of the following papers which will be published by my collaborators.

In previous papers by Misra(1) and by Born and Misra(2) lattice sums of the type required in discussing the stability of a cubic crystal of the Bravais type in which the forces are central have been calculated. In the investigation of the thermodynamic properties of crystals a more general type of lattice sum occurs, which involves the phases of the waves. In the present paper a method of calculating these sums is developed and tables are computed.

Assuming that the solute and solvent molecules in a solution can be regarded as occupying sites on a regular lattice and that the potential energy arises from interactions between molecules which occupy closest neighbour sites, the vapour-pressure equations have been determined for solutions in which each solute molecule contains three groups (or submolecules) and occupies three lattice sites in such a way that successive submolecules occupy closest neighbour sites on the lattice while each solvent molecule occupies only one site. The vapour-pressure equations are compared with those which have already been obtained by Fowler and Guggenheim for the case in which each solute molecule contains two submolecules in order to determine the effect on the form of the vapour-pressure equations of the number of submolecules in each solute molecule. This enables the determination of the vapour-pressure equations when each solute molecule contains n submolecules and occupies n lattice sites in such a way that successive submolecules occupy closest neighbour sites on the lattice. In this latter case the vapour-pressure equations are

These equations are used to determine the osmotic pressure of solutions of long-chain polymers, and it is found that in the region of osmotic interest, the osmotic pressure is given by an equation of the form

where c g. of solute per 100 c.c. of solution is the concentration. It is shown that this equation can be written approximately

which is the quadratic relation which has usually been fitted to osmotic measurements. To this approximation π/c plotted as a function of c gives a straight line of which the intercept on the π/c axis determines the molecular weight of the polymer molecule and the gradient determines the number of submolecules in each polymer molecule.

On an algebraic surface f of order n in space of three dimensions, the canonical system | k | of curves is traced by all those surfaces π of order n − 4 which fulfil certain conditions of adjunction at the singularities of f: for example, which pass simply through the double curves and through the isolated tacnodes of f; which pass doubly through the isolated fourfold points of f; and so on. The assigned fixed points and curves of the adjoint surfaces ø at these singularities of f are not taken to be part of the canonical system | k |; but | k | may have unassigned fixed parts e. Three cases are usually (3) distinguished.

Let L1, L2, L3 be three homogeneous linear forms in u, v, w with real coefficients and determinant 1. Let M denote the lower bound of

for integral values of u, v, w, not all zero. I proved a few years ago (1) that

more precisely, that

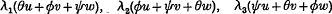
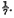except when L1, L2, L3 are of a special type, in which case If we denote by θ, ø, ψ the roots of the cubic equation t3+t2-2t-1 = 0, the special linear forms are equivalent, by an integral unimodular linear transformation, to

(in any order), where λ1,λ2,λ3 are real number whose product is In this case, L1L2L3|λ1λ2λ3 is a non-zero integer, and the minimum of its absolute value is 1, giving

The fact that the prime ideal associated with a given irreducible algebraic variety has a finite basis is a pure existence theorem. Only in a few isolated particular cases has the base for the ideal been found, and there appears to be no general method for determining the base which can be carried out in practice. Hilbert, who initiated the theory, proved that the prime ideal defining the ordinary twisted cubic curve has a base consisting of three quadrics, and contributions to the ideal theory of algebraic varieties have been made by König, Lasker, Macaulay and, more recently, by Zariski. A good summary, from the viewpoint of a geometer, is given by Bertini [(1), Chapter XII]. However, the tendency has been towards the development of the pure theory. In the following paper we actually find the bases for the prime ideals associated with certain classes of algebraic varieties. The paper falls into two parts. In Part I there is proved a theorem (the Principal Theorem) of wide generality, and then examples are given of some classes of varieties satisfying the conditions of the theorem. In Part II we find the base for the prime ideals associated with Veronesean varieties and varieties of Segre. The latter are particularly interesting since they represent (1, 1), without exception, the points of a multiply-projective space.