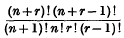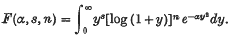Refine search
Actions for selected content:
26232 results in Theoretical Physics and Mathematical Physics
PSP volume 38 issue 3 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 3 / July 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- July 1942
-
- Article
-
- You have access
- Export citation
PSP volume 38 issue 3 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 3 / July 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- July 1942
-
- Article
-
- You have access
- Export citation
PSP volume 38 issue 2 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 2 / April 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- April 1942
-
- Article
-
- You have access
- Export citation
A remark on a property of a special pencil of quadrics
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 2 / April 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 234-235
- Print publication:
- April 1942
-
- Article
- Export citation
Note on the degeneration of algebraic varieties
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 2 / April 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 231-233
- Print publication:
- April 1942
-
- Article
- Export citation
The thermodynamic derivation of Fowler's adsorption isotherm
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 2 / April 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 236-239
- Print publication:
- April 1942
-
- Article
- Export citation
On Lorentz invariance in the quantum theory
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 2 / April 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 193-200
- Print publication:
- April 1942
-
- Article
- Export citation
PSP volume 38 issue 2 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 2 / April 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- April 1942
-
- Article
-
- You have access
- Export citation
On Hausdorff's methods of summability
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 2 / April 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 166-192
- Print publication:
- April 1942
-
- Article
- Export citation
On the determination of intermolecular energies by inductive analysis
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 2 / April 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 224-230
- Print publication:
- April 1942
-
- Article
- Export citation
Some relations between certain methods of summation of infinite series
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 2 / April 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 144-164
- Print publication:
- April 1942
-
- Article
- Export citation
A note on k-connexes
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 2 / April 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 129-143
- Print publication:
- April 1942
-
- Article
- Export citation
Two-centre integrals occurring in the theory of molecular structure
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 2 / April 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 210-223
- Print publication:
- April 1942
-
- Article
- Export citation
On Lorentz invariance in the quantum theory. II
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 2 / April 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 201-209
- Print publication:
- April 1942
-
- Article
- Export citation
Relations between concentrated sets and sets possessing property C
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 1 / January 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 20-23
- Print publication:
- January 1942
-
- Article
- Export citation
On the stability of crystal lattices IX. Covariant theory of lattice deformations and the stability of some hexagonal lattices
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 1 / January 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 82-99
- Print publication:
- January 1942
-
- Article
- Export citation
PSP volume 38 issue 1 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 1 / January 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- January 1942
-
- Article
-
- You have access
- Export citation
A theorem on s-dimensional measure of sets of points
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 1 / January 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 24-27
- Print publication:
- January 1942
-
- Article
- Export citation
On the stability of crystal lattices VIII. Stability of rhombohedral Bravais lattices*
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 1 / January 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 67-81
- Print publication:
- January 1942
-
- Article
- Export citation
Expansions for a particular class of exponential-logarithmic integrals
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 38 / Issue 1 / January 1942
- Published online by Cambridge University Press:
- 24 October 2008, pp. 34-39
- Print publication:
- January 1942
-
- Article
- Export citation
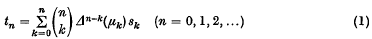
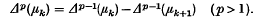


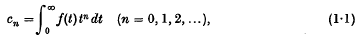
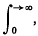 or possibly
or possibly 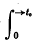 if
if