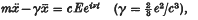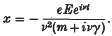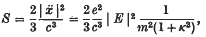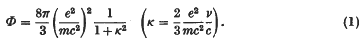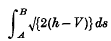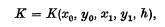Refine search
Actions for selected content:
26232 results in Theoretical Physics and Mathematical Physics
Notes on the two-centre problem in wave mechanics: II. Some new solutions of the wave equation
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 4 / October 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 384-396
- Print publication:
- October 1941
-
- Article
- Export citation
Momentum distribution in molecular systems: Part V. Momentum distribution and the shape of the Compton line for CH4, C2H6, C2H4 and C2H2
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 4 / October 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 406-421
- Print publication:
- October 1941
-
- Article
- Export citation
Note on semi-groups
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 4 / October 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 434-435
- Print publication:
- October 1941
-
- Article
- Export citation
A proof of the theorem of the double-six
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 4 / October 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 433-434
- Print publication:
- October 1941
-
- Article
- Export citation
On the subadditivity of the transfinite diameter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 4 / October 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 373-383
- Print publication:
- October 1941
-
- Article
- Export citation
On average values of arithmetic functions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 4 / October 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 358-372
- Print publication:
- October 1941
-
- Article
- Export citation
The quantum theory of radiation damping‡
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 3 / July 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 301-316
- Print publication:
- July 1941
-
- Article
- Export citation
The probability distribution of the extent of a random chain
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 3 / July 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 244-251
- Print publication:
- July 1941
-
- Article
- Export citation
On the generalized helices of Hayden and Sypták in an N-space
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 3 / July 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 229-243
- Print publication:
- July 1941
-
- Article
- Export citation
A new type of disintegration produced by deuterons
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 3 / July 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 317-323
- Print publication:
- July 1941
-
- Article
- Export citation
PSP volume 37 issue 3 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 3 / July 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- July 1941
-
- Article
-
- You have access
- Export citation
PSP volume 37 issue 3 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 3 / July 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- July 1941
-
- Article
-
- You have access
- Export citation
On the theory of the liquid state: III. The hole theory of the viscous flow of liquids
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 3 / July 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 281-290
- Print publication:
- July 1941
-
- Article
- Export citation
On the theory of the liquid state: I. The statistical treatment of the thermodynamics of liquids by the theory of holes
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 3 / July 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 252-275
- Print publication:
- July 1941
-
- Article
- Export citation
The influence of radiation damping on the scattering of light and mesons by free particles. I
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 3 / July 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 291-300
- Print publication:
- July 1941
-
- Article
- Export citation
On the theory of the liquid state: II. Application of the hole theory to superheated liquids and supersaturated solutions of gases in liquids
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 3 / July 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 276-280
- Print publication:
- July 1941
-
- Article
- Export citation
The fractional dimensional theory of continued fractions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 3 / July 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 199-228
- Print publication:
- July 1941
-
- Article
- Export citation
The action in a uniform field
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 2 / April 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 168-176
- Print publication:
- April 1941
-
- Article
- Export citation
The motion of a solid through an infinite liquid under no forces
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 2 / April 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 150-167
- Print publication:
- April 1941
-
- Article
- Export citation
The reflexion of sound pulses by convex parabolic reflectors
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 37 / Issue 2 / April 1941
- Published online by Cambridge University Press:
- 24 October 2008, pp. 134-149
- Print publication:
- April 1941
-
- Article
- Export citation
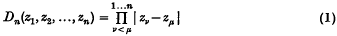
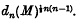 Then it can be proved that
Then it can be proved that
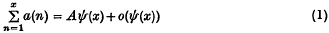
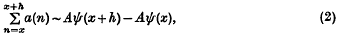

 taking place, in all probability, through the formation of a ‘compound nucleus’ of the Bohr type.
taking place, in all probability, through the formation of a ‘compound nucleus’ of the Bohr type.