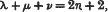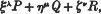Refine search
Actions for selected content:
26204 results in Theoretical Physics and Mathematical Physics
The effects produced by positive ion bombardment of solids: metallic ions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 3 / July 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 451-469
- Print publication:
- July 1928
-
- Article
- Export citation
PSP volume 24 issue 3 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 3 / July 1928
- Published online by Cambridge University Press:
- 24 October 2008, p. b1
- Print publication:
- July 1928
-
- Article
-
- You have access
- Export citation
Note on Pauli's Exclusion Principle
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 3 / July 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 445-446
- Print publication:
- July 1928
-
- Article
- Export citation
On the Connexion of a Certain Identity with the Extension of Conical Order to n Dimensions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 3 / July 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 357-374
- Print publication:
- July 1928
-
- Article
- Export citation
On the periods of a free-free bar immersed in water
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 3 / July 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 400-413
- Print publication:
- July 1928
-
- Article
- Export citation
PSP volume 24 issue 3 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 3 / July 1928
- Published online by Cambridge University Press:
- 24 October 2008, p. f1
- Print publication:
- July 1928
-
- Article
-
- You have access
- Export citation
The Wave Mechanics of an Atom with a non-Coulomb Central Field. Part III. Term Values and Intensities in Series in Optical Spectra
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 3 / July 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 426-437
- Print publication:
- July 1928
-
- Article
- Export citation
The motion of a particle in a periodic field of force
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 3 / July 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 447-450
- Print publication:
- July 1928
-
- Article
- Export citation
The influence of different nuclei on the absorption spectra of organic compounds
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 3 / July 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 421-425
- Print publication:
- July 1928
-
- Article
- Export citation
A Method of Generalising the Law of Mass Action for Heterogeneous Surface Reactions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 2 / April 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 307-314
- Print publication:
- April 1928
-
- Article
- Export citation
Some Applications and Implications of Duane's Quantum Theory of Diffraction
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 2 / April 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 343-356
- Print publication:
- April 1928
-
- Article
- Export citation
On the Action of the Geiger α-particle Counter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 2 / April 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 251-258
- Print publication:
- April 1928
-
- Article
- Export citation
The Specific Heat of Carbon Dioxide—Correction
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 2 / April 1928
- Published online by Cambridge University Press:
- 24 October 2008, p. 290
- Print publication:
- April 1928
-
- Article
- Export citation
Relation between Mean Stopping Power and Mean Range of β-rays.
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 2 / April 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 315-319
- Print publication:
- April 1928
-
- Article
- Export citation
Extension of a Lemma of Stroh
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 2 / April 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 218-222
- Print publication:
- April 1928
-
- Article
- Export citation
A recording gyroscope
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 2 / April 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 236-250
- Print publication:
- April 1928
-
- Article
- Export citation
PSP volume 24 issue 2 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 2 / April 1928
- Published online by Cambridge University Press:
- 24 October 2008, p. b1
- Print publication:
- April 1928
-
- Article
-
- You have access
- Export citation
On the present position of the Theory of Centres of Activity in Heterogeneous Catalysis
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 2 / April 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 291-306
- Print publication:
- April 1928
-
- Article
- Export citation
The Photo-Electric Threshold and the Heat of Dissociation of the Potassium Molecule
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 2 / April 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 320-327
- Print publication:
- April 1928
-
- Article
- Export citation
Limiting forms of the frequency distribution of the largest or smallest member of a sample
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 2 / April 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 180-190
- Print publication:
- April 1928
-
- Article
- Export citation
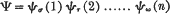
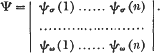
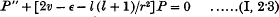
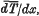 , where
, where 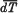 is the mean energy lost by β-rays of energy
is the mean energy lost by β-rays of energy 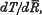 , where
, where 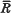 is the mean range of particles of energy
is the mean range of particles of energy