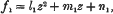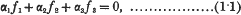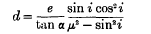Refine search
Actions for selected content:
26203 results in Theoretical Physics and Mathematical Physics
An Asymptotic Expansion for
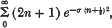
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 2 / April 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 280-289
- Print publication:
- April 1928
-
- Article
- Export citation
On the Formation of a Gaseous Helide of Radium Active Deposit
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 2 / April 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 268-275
- Print publication:
- April 1928
-
- Article
- Export citation
On the quintic surface in space of five dimensions. (Part II, Curves on the surface.*)
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 2 / April 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 191-209
- Print publication:
- April 1928
-
- Article
- Export citation
Operational Solution of Some Problems in Viscous Fluid Motion
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 2 / April 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 231-235
- Print publication:
- April 1928
-
- Article
- Export citation
The average value of an exponential function over the lattice points of a circle
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 2 / April 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 171-179
- Print publication:
- April 1928
-
- Article
- Export citation
The High-frequency Electric Discharge at Low Pressures
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 2 / April 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 259-267
- Print publication:
- April 1928
-
- Article
- Export citation
A dynamical method for the determination of Young's modulus by stretching
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 2 / April 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 276-279
- Print publication:
- April 1928
-
- Article
- Export citation
The Second Solution of Mathieu's Differential Equation
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 2 / April 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 223-230
- Print publication:
- April 1928
-
- Article
- Export citation
PSP volume 24 issue 2 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 2 / April 1928
- Published online by Cambridge University Press:
- 24 October 2008, p. f1
- Print publication:
- April 1928
-
- Article
-
- You have access
- Export citation
An Involution in the Complex Variable
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 2 / April 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 210-217
- Print publication:
- April 1928
-
- Article
- Export citation
On the arc spectrum of antimony
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 1 / January 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 85-88
- Print publication:
- January 1928
-
- Article
- Export citation
PSP volume 24 issue 1 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 1 / January 1928
- Published online by Cambridge University Press:
- 24 October 2008, p. b1
- Print publication:
- January 1928
-
- Article
-
- You have access
- Export citation
The Wave Mechanics of an Atom with a Non-Coulomb Central Field. Part I. Theory and Methods
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 1 / January 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 89-110
- Print publication:
- January 1928
-
- Article
- Export citation
The Specific Heat of Hydrogen at high temperatures
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 1 / January 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 80-84
- Print publication:
- January 1928
-
- Article
- Export citation
On the Structure of Liquids and Vitreous Solids
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 1 / January 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 19-31
- Print publication:
- January 1928
-
- Article
- Export citation
On the quintic surface in space of five dimensions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 1 / January 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 48-55
- Print publication:
- January 1928
-
- Article
- Export citation
Note on Losses in Cable Sheaths
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 1 / January 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 65-73
- Print publication:
- January 1928
-
- Article
- Export citation
The Interference of Light in a Wedge
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 1 / January 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 150-165
- Print publication:
- January 1928
-
- Article
- Export citation
On Reichinstein's Displacement Principle
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 1 / January 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 56-64
- Print publication:
- January 1928
-
- Article
- Export citation
Extension of a set of theorems in circle geometry
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 1 / January 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 10-18
- Print publication:
- January 1928
-
- Article
- Export citation