Article contents
Percolation and Connectivity in AB Random Geometric Graphs
Published online by Cambridge University Press: 04 January 2016
Abstract
Given two independent Poisson point processes Φ(1), Φ(2) in 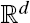 , the AB Poisson Boolean model is the graph with the points of Φ(1) as vertices and with edges between any pair of points for which the intersection of balls of radius 2r centered at these points contains at least one point of Φ(2). This is a generalization of the AB percolation model on discrete lattices. We show the existence of percolation for all d ≥ 2 and derive bounds for a critical intensity. We also provide a characterization for this critical intensity when d = 2. To study the connectivity problem, we consider independent Poisson point processes of intensities n and τn in the unit cube. The AB random geometric graph is defined as above but with balls of radius r. We derive a weak law result for the largest nearest-neighbor distance and almost-sure asymptotic bounds for the connectivity threshold.
, the AB Poisson Boolean model is the graph with the points of Φ(1) as vertices and with edges between any pair of points for which the intersection of balls of radius 2r centered at these points contains at least one point of Φ(2). This is a generalization of the AB percolation model on discrete lattices. We show the existence of percolation for all d ≥ 2 and derive bounds for a critical intensity. We also provide a characterization for this critical intensity when d = 2. To study the connectivity problem, we consider independent Poisson point processes of intensities n and τn in the unit cube. The AB random geometric graph is defined as above but with balls of radius r. We derive a weak law result for the largest nearest-neighbor distance and almost-sure asymptotic bounds for the connectivity threshold.
MSC classification
Information
- Type
- Stochastic Geometry and Statistical Applications
- Information
- Copyright
- © Applied Probability Trust
Footnotes
Research supported in part by UGC SAP-IV and DRDO, grant no. DRDO/PAM/SKI/593.
Supported in part by a grant from EADS, France, Israel Science foundation (grant no. 853/10), and AFOSR (grant no. FA8655-11-1-3039).
References
- 9
- Cited by

