Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Khurana, Anjana
Khurana, Dinesh
and
Nielsen, Pace P.
2019.
Symmetries in idempotent factorizations.
Journal of Algebra and Its Applications,
Vol. 18,
Issue. 05,
p.
1950084.
Ke, Yuanyuan
Chen, Jianlong
Stanimirović, Predrag
and
Ćirić, Miroslav
2021.
Characterizations and representations of outer inverse for matrices over a ring.
Linear and Multilinear Algebra,
Vol. 69,
Issue. 1,
p.
155.
Wu, Cang
and
Chen, Jianlong
2022.
Left core inverses in rings with involution.
Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas,
Vol. 116,
Issue. 2,
Lam, T. Y.
2023.
An introduction to q-central idempotents and q-abelian rings.
Communications in Algebra,
Vol. 51,
Issue. 3,
p.
1071.
Wu, Cang
and
Chen, Jianlong
2023.
A class of outer generalized inverses and a note on Drazin’s finiteness conditions in rings and semigroups.
Communications in Algebra,
Vol. 51,
Issue. 12,
p.
5167.
Khurana, Dinesh
and
Lam, T.Y.
2024.
Ring elements of stable range one.
Journal of Algebra,
Vol. 652,
Issue. ,
p.
208.
Lam, T. Y.
2024.
On some generalizations of abelian rings.
Journal of Algebra and Its Applications,
Vol. 23,
Issue. 08,
 $a$ in a Dedekind-finite ring
$a$ in a Dedekind-finite ring 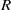 $R$ satisfying
$R$ satisfying 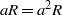 $aR= {a}^{2} R$ also satisfies
$aR= {a}^{2} R$ also satisfies 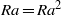 $Ra= R{a}^{2} $. In this paper, we answer this question in the negative. We also prove that if
$Ra= R{a}^{2} $. In this paper, we answer this question in the negative. We also prove that if  $a$ is an element of a Dedekind-finite exchange ring
$a$ is an element of a Dedekind-finite exchange ring 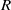 $R$ and
$R$ and 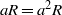 $aR= {a}^{2} R$, then
$aR= {a}^{2} R$, then 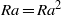 $Ra= R{a}^{2} $. This gives an easier proof of Dischinger’s theorem that left strongly
$Ra= R{a}^{2} $. This gives an easier proof of Dischinger’s theorem that left strongly 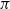 $\pi $-regular rings are right strongly
$\pi $-regular rings are right strongly 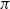 $\pi $-regular, when it is already known that
$\pi $-regular, when it is already known that 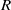 $R$ is an exchange ring.
$R$ is an exchange ring.