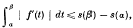Refine listing
Actions for selected content:
Most read
This page lists the top ten most read articles for this journal based on the number of full text views and downloads recorded on Cambridge Core over the last 90 days. This list is updated on a daily basis.
Contents
The Numerically Greatest Term of a Binomial Expansion
-
- Journal:
- Edinburgh Mathematical Notes / Volume 7 / 1911
- Published online by Cambridge University Press:
- 31 October 2008, pp. 74-77
-
- Article
-
- You have access
- Export citation
An Elementary Proof of Morley's Trisector Theorem
-
- Journal:
- Edinburgh Mathematical Notes / Volume 34 / 1944
- Published online by Cambridge University Press:
- 31 October 2008, pp. 12-13
-
- Article
-
- You have access
- Export citation
An Expansion for xn + yn
-
- Journal:
- Edinburgh Mathematical Notes / Volume 34 / 1944
- Published online by Cambridge University Press:
- 31 October 2008, pp. 14-15
-
- Article
-
- You have access
- Export citation
Dirichlet's Integrals
-
- Journal:
- Edinburgh Mathematical Notes / Volume 34 / 1944
- Published online by Cambridge University Press:
- 31 October 2008, pp. 15-17
-
- Article
-
- You have access
- Export citation
The characteristic polynomials of AB and BA
-
- Journal:
- Edinburgh Mathematical Notes / Volume 39 / 1954
- Published online by Cambridge University Press:
- 31 October 2008, p. 13
-
- Article
-
- You have access
- Export citation
On the Number of Distinct Terms in the Expansion of Symmetric and Skew Determinants
-
- Journal:
- Edinburgh Mathematical Notes / Volume 34 / 1944
- Published online by Cambridge University Press:
- 31 October 2008, pp. 1-5
-
- Article
-
- You have access
- Export citation
An Elementary Proof of Feuerbach's Theorem
-
- Journal:
- Edinburgh Mathematical Notes / Volume 22 / 1924
- Published online by Cambridge University Press:
- 31 October 2008, pp. 11-12
-
- Article
-
- You have access
- Export citation
Principal radii of curvature at a point on an ellipsoid
-
- Journal:
- Edinburgh Mathematical Notes / Volume 24 / 1929
- Published online by Cambridge University Press:
- 31 October 2008, pp. xvi-xvii
-
- Article
-
- You have access
- Export citation
A note on rectifiable curves
-
- Journal:
- Edinburgh Mathematical Notes / Volume 40 / 1956
- Published online by Cambridge University Press:
- 31 October 2008, pp. 12-14
-
- Article
-
- You have access
- Export citation
A necessary and sufficient condition for differentiability
-
- Journal:
- Edinburgh Mathematical Notes / Volume 37 / 1949
- Published online by Cambridge University Press:
- 31 October 2008, pp. 13-16
-
- Article
-
- You have access
- Export citation
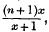 sometimes
sometimes 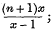 ; and unless the student has a very good memory he is sure sometimes to make mistakes. Elementary mathematics ought not to be a memory exercise. It is a platitude to say that the educational value of the teaching of mathematics lies in its training of the powers of reasoning. This element is eliminated when processes of reasoning are reduced to a rule of thumb. As well might one use “Molesworth” as a text-book of the principles of mechanics.
; and unless the student has a very good memory he is sure sometimes to make mistakes. Elementary mathematics ought not to be a memory exercise. It is a platitude to say that the educational value of the teaching of mathematics lies in its training of the powers of reasoning. This element is eliminated when processes of reasoning are reduced to a rule of thumb. As well might one use “Molesworth” as a text-book of the principles of mechanics.