Hostname: page-component-7dd5485656-kp629 Total loading time: 0 Render date: 2025-10-29T22:57:21.909Z Has data issue: false hasContentIssue false
  • English
  • Français

On uniqueness of invariant measures for random walks on 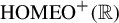${\textup {HOMEO}}^+(\mathbb R)$

Part of: Ergodic theory Markov processes Random dynamical systems

Published online by Cambridge University Press:  29 April 2021

SARA BROFFERIO ,
DARIUSZ BURACZEWSKI Open the ORCID record for DARIUSZ BURACZEWSKI [Opens in a new window]  and
TOMASZ SZAREK
SARA BROFFERIO
Affiliation:
Laboratoire de Mathématiques, Université Paris-Sacley, Campus d’Orsay, Gif-sur-Yvette, France (e-mail: sara.brofferio@gmail.com)
DARIUSZ BURACZEWSKI*
Affiliation:
Mathematical Institute University of Wrocław, Pl. Grunwaldzki 2/4, 50-384 Wrocław, Poland
TOMASZ SZAREK
Affiliation:
Institute of Mathematics, Polish Academy of Sciences, Abrahama 18, 81-967 Sopot, Poland (e-mail: tszarek@impan.pl)
*
e-mail: dariusz.buraczewski@uwr.edu.pl
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider random walks on the group of orientation-preserving homeomorphisms of the real line 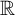${\mathbb R}$. In particular, the fundamental question of uniqueness of an invariant measure of the generated process is raised. This problem was studied by Choquet and Deny [Sur l’équation de convolution 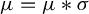$\mu = \mu * \sigma $. C. R. Acad. Sci. Paris 250 (1960), 799–801] in the context of random walks generated by translations of the line. Nowadays the answer is quite well understood in general settings of strongly contractive systems. Here we focus on a broader class of systems satisfying the conditions of recurrence, contraction and unbounded action. We prove that under these conditions the random process possesses a unique invariant Radon measure on 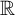${\mathbb R}$. Our work can be viewed as following on from Babillot et al [The random difference equation 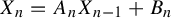$X_n=A_n X_{n-1}+B_n$ in the critical case. Ann. Probab. 25(1) (1997), 478–493] and Deroin et al [Symmetric random walk on 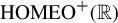$\mathrm {HOMEO}^{+}(\mathbb {R})$. Ann. Probab. 41(3B) (2013), 2066–2089].

Keywords

ergodic measuregroup of homeomorphismsinvariant measurerandom walks

MSC classification

Primary: 60J05: Discrete-time Markov processes on general state spaces
Secondary: 37H99: None of the above, but in this section 37A05: Measure-preserving transformations

Information

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 7 , July 2022 , pp. 2207 - 2238
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0), which permits unrestricted re-use, distribution and reproduction, provided the original article is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

References

Alsedà, L. and Misiurewicz, M.. Random interval homeomorphisms. Publ. Mat. 58 (2014), 15–36.CrossRefGoogle Scholar
Alsmeyer, G.. On the stationary tail index of iterated random Lipschitz functions. Stochastic Process. Appl. 126(1) (2016), 209–233.CrossRefGoogle Scholar
Alsmeyer, G., Brofferio, S. and Buraczewski, D.. Asymptotically linear iterated function systems on the real line. Preprint, 2021, arXiv:2102.02299.Google Scholar
Avila, A. and Viana, M.. Extremal Lyapunov exponents: an invariance principle and applications. Invent. Math. 181(1) (2010), 115–178.CrossRefGoogle Scholar
Babillot, M., Bougerol, P. and Elie, L.. The random difference equation ${X}_n={A}_n{X}_{n-1}+{B}_n$ in the critical case. Ann. Probab. 25(1) (1997), 478–493.CrossRefGoogle Scholar
Benda, M.. Schwach kontraktive dynamische Systeme. PhD Thesis, Ludwig-Maximilians-Universität München, 1998.Google Scholar
Brofferio, S.. How a centred random walk on the affine group goes to infinity. Ann. Inst. Henri Poincaré Probab. Stat. 39(3) (2003), 371–384.CrossRefGoogle Scholar
Brofferio, S. and Buraczewski, D.. On unbounded invariant measures of stochastic dynamical systems. Ann. Probab. 41(3) (2015), 1456–1492.Google Scholar
Buraczewski, D., Damek, E. and Mikosch, T.. Stochastic Models with Power-Law Tails. The Equation $X= AX+B$ . (Springer Series in Operations Research and Financial Engineering). Springer, Cham, 2016.CrossRefGoogle Scholar
Czudek, K. and Szarek, T.. Ergodicity and central limit theorem for random interval homeomorphisms. Israel J. Math. 239 (2020), 75–98.CrossRefGoogle Scholar
Chacon, R. V. and Ornstein, D. S.. A general ergodic theorem. Illinois J. Math. 4 (1960), 153–160.CrossRefGoogle Scholar
Choquet, G. and Deny, J.. Sur l’équation de convolution $\mu =\mu \ast \sigma$ . C. R. Acad. Sci. Paris 250 (1960), 799–801.Google Scholar
Deroin, B., Kleptsyn, V., Navas, A. and Parwani, K.. Symmetric random walk on ${{\mathrm{HOMEO}}}^{+}\left(\mathbb{R}\right)$ . Ann. Probab. 41(3B) (2013), 2066–2089.CrossRefGoogle Scholar
Diaconis, P. and Freedman, D.. Iterated random functions. SIAM Rev. 41(1) (1999), 45–76.CrossRefGoogle Scholar
Durrett, R.. Probability—Theory and Examples. (Cambridge Series in Statistical and Probabilistic Mathematics, 49), 5th edn. Cambridge University Press, Cambridge, 2019.CrossRefGoogle Scholar
Foguel, S. R.. The Ergodic Theory of Markov Processes (Van Nostrand Mathematical Studies, 21). Van Nostrand Reinhold Co., New York, 1969.Google Scholar
Furstenberg, H.. Noncommuting random products. Trans. Amer. Math. Soc. 108 (1963), 377–428.CrossRefGoogle Scholar
Garsia, A. M.. Topics in Almost Everywhere Lonvergence (Lectures in Advanced Mathematics, 4). Markham Publishing Co., Chicago, 1970.Google Scholar
Gharaei, M. and Homburg, A. I.. Random interval diffeomorphisms. Discrete Contin. Dyn. Syst. Ser. S 10(2) (2017), 241–272.Google Scholar
Goldie, C. M.. Implicit renewal theory and tails of solutions of random equations. Ann. Appl. Probab. 1(1) (1991), 126–166.CrossRefGoogle Scholar
Greschonig, G. and Schmidt, K.. Ergodic decomposition of quasi-invariant probability measures. Colloq. Math. 84 /85 (2000), part 2, 495–514.CrossRefGoogle Scholar
Letac, G.. A contraction principle for certain Markov chains and its applications. Random Matrices and Their Applications (Brunswick, ME, 1984) (Contemporary Mathematics, 50). American Mathematical Society, Providence, RI, 1986, pp. 263–273.CrossRefGoogle Scholar
Lin, M.. Conservative Markov processes on a topological space. Israel J. Math. 8 (1970), 165–186.CrossRefGoogle Scholar
Malicet, D.. Random walks on Homeo $({S}^1)$ . Commun. Math. Phys. 356(3) (2017), 1083–1116.CrossRefGoogle Scholar
Meyn, S. and Tweedie, R. L.. Markov Chains and Stochastic Stability, 2nd edn. Cambridge University Press, Cambridge, 2009. With a prologue by P. W. Glynn.Google Scholar
Peigné, M. and Woess, W.. Stochastic dynamical systems with weak contractivity properties I. Strong and local contractivity. Colloq. Math. 125(1) (2011), 31–54.CrossRefGoogle Scholar
Peigné, M. and Woess, W.. Stochastic dynamical systems with weak contractivity properties II. Iteration of Lipschitz mappings. Colloq. Math. 125(1) (2011), 55–81.CrossRefGoogle Scholar
Pène, F. and Thomine, D.. Probabilistic potential theory and induction of dynamical systems. Preprint, 2019, arXiv:1909.05518.Google Scholar
Revuz, D.. Markov Chains (North-Holland Mathematical Library, 11), 2nd edn. North-Holland Publishing Co., Amsterdam, 1984.Google Scholar
Zweimüller, R.. Survey Notes on Infinite Ergodic Theory. https://mat.univie.ac.at/zweimueller/MyPub/SurreyNotes.pdf.Google Scholar