We investigate the asymptotic sample path behaviour of a randomly perturbed discrete-time dynamical system. We consider the case where the trajectories of the non-perturbed dynamical system are attracted by a finite number of limit sets and characterize a case where this property remains valid for the perturbed dynamical system when the perturbation converges to zero. For this purpose, no further assumptions on the perturbation are needed and our main condition applies to the limit sets of the non-perturbed dynamical system. When the limit sets reduce to limit points we show that this main condition is more general than the usual assumption of the existence of a Lyapunov function for the non-perturbed dynamical system. An application to an epidemic model is given to illustrate our results.

Stochastic models for the origin and extinction of species have been rather neglected in applied probability. As an alternative to modelling speciation and extinction as intrinsically random, I shall describe and show simulations of a rulebased model. This involves mathematical representations of notions such as genetic type of species, environmental niche, fitness of a species in a niche, and adaptation. There are underlying random mechanisms for changes of niche sizes and for disconnection and reconnection of geographical regions, and these ultimately drive the evolution of species.

Other approaches to mathematical modelling of evolution are briefly mentioned.

We give a unified presentation of stability results for stochastic vector difference equations 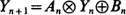based on various choices of binary operations 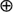and 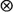, assuming that 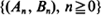are stationary and ergodic. In the scalar case, under standard addition and multiplication, the key condition for stability is E [log |A 0|] < 0. In the generalizations, the condition takes the form γ< 0, where γis the limit of a subadditive process associated with 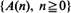. Under this and mild additional conditions, the process 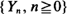has a unique finite stationary distribution to which it converges from all initial conditions.

The variants of standard matrix algebra we consider replace the operations + and × with (max, +), (max,×), (min, +), or (min,×). In each case, the appropriate stability condition parallels that for the standard recursions, involving certain subadditive limits. Since these limits are difficult to evaluate, we provide bounds, thus giving alternative, computable conditions for stability.

The functional differential equation y′(x) = ay(λx) + by(x) arises in many different situations. The purpose of this note is to show how it arises in some multitype branching process cell population models. We also show how its solution can be given an intuitive interpretation as the probability density function of an infinite sum of independent but not identically distributed random variables.

The DNA of higher animals replicates by an interesting mechanism. Enzymes recognise specific sites randomly scattered on the molecule and establish a bidirectional process of unwinding and replication from these sites. We investigate the limiting distribution of the completion time for this process by considering related coverage problems investigated by Janson (1983) and Hall (1988).

We consider non-homogeneous Markov chains generated by the simulated annealing algorithm. We classify states according to asymptotic properties of trajectories. We identify recurrent and transient states. The set of recurrent states is partitioned into disjoint classes of asymptotically communicating states. These classes correspond to atoms of the tail sigma-field. The results are valid under the weak reversibility assumption of Hajek.

Models for epidemic spread of infections are formulated by defining intensities for relevant counting processes. It is assumed that an infected individual passes through k stages of infectivity. The times spent in the different stages are random. Many well-known models for the spread of infections can be described in this way. The models can also be applied to describe other processes of epidemic character (such as models for rumour spreading). Asymptotic results are derived both for the size and for the duration of the epidemic.

We consider a stochastic model for the spread of an epidemic amongst a closed homogeneously mixing population, in which there are several different types of infective, each newly infected individual choosing its type at random from those available. The model is based on the carrier-borne model of Downton (1968), as extended by Picard and Lefèvre (1990). The asymptotic distributions of final size and area under the trajectory of infectives are derived as the initial population becomes large, using arguments based on those of Scalia-Tomba (1985), (1990). We then use our limiting results to compare the asymptotic final size distribution of our model with that of a related multi-group model, in which the type of each infective is assigned deterministically.

Consider a stationary Markov chain with state space consisting of the ξ -letter alphabet set Λ= {a 1 , a 2, ···, aξ }. We study the variables M=M(n, k) and N=N(n, k), defined, respectively, as the number of overlapping and non-overlapping occurrences of a fixed periodic k-letter word, and use the Stein–Chen method to obtain compound Poisson approximations for their distribution.

We consider a stochastic model for the spread of a carrier-borne epidemic amongst a closed homogeneously mixing population, in which a proportion 1 − π of infected susceptibles are directly removed and play no part in spreading the infection. The remaining proportion π become carriers, with an infectious period that follows an arbitrary but specified distribution. We give a construction of the epidemic process which directly exploits its probabilistic structure and use it to derive the exact joint distribution of the final size and severity of the carrier-borne epidemic, distinguishing between removed carriers and directly removed individuals. We express these results in terms of Gontcharoff polynomials. When the infectious period follows an exponential distribution, our model reduces to that of Downton (1968), for which we use our construction to derive an explicit expression for the time-dependent state probabilities.

Asymptotic formulas for means and variances of a multitype decomposable age-dependent supercritical branching process are derived. This process is a generalization of the Kendall–Neyman–Scott two-stage model for tumor growth. Both means and variances have exponential growth rates as in the case of the Markov branching process. But unlike Markov branching, these asymptotic moments depend on the age of the original individual at the start of the process and the life span distribution of the progenies.

We show that if the limiting conditional distribution for an absorbed birth–death chain exists, then the chain conditioned to non-absorption converges to a Markov chain with transition probabilities given by the matrix associated with the minimal quasi-stationary distribution.

The method earlier introduced for one-dimensional diffusion processes [6] is extended to obtain closed form expressions for the transition p.d.f.'s of two-dimensional diffusion processes in the presence of absorbing boundaries and for the first-crossing time p.d.f.'s through such boundaries. Use of such a method is finally made to analyse a two-dimensional linear process.

Under the assumptions of the neutral infinite alleles model, K (the total number of alleles present in a sample) is sufficient for estimating θ (the mutation rate). This is a direct result of the Ewens sampling formula, which gives a consistent, asymptotically normal estimator for θ based on K. It is shown that the same estimator used to estimate θ under neutrality is consistent and asymptotically normal, even when the assumption of selective neutrality is violated.

We prove that every infinite-state stochastic matrix P say, that is irreducible and consists of positive-recurrrent states can be represented in the form I – P=(A – I)(B – S), where A is strictly upper-triangular, B is strictly lower-triangular, and S is diagonal. Moreover, the elements of A are expected values of random variables that we will specify, and the elements of B and S are probabilities of events that we will specify. The decomposition can be used to obtain steady-state probabilities, mean first-passage-times and the fundamental matrix.

One result that is of both theoretical and practical importance regarding point processes is the method of thinning. The basic idea of this method is that under some conditions, there exists an embedded Poisson process in any point process such that all its arrival points form a sub-sequence of the Poisson process. We extend this result by showing that on the embedded Poisson process of a uni- or multi-variable marked point process in which interarrival time distributions may depend on the marks, one can define a Markov chain with a discrete state that characterizes the stage of the interarrival times. This implies that one can construct embedded Markov chains with countable state spaces for the state processes of many practical systems that can be modeled by such point processes.

We consider the problem of conditioning a continuous-time Markov chain (on a countably infinite state space) not to hit an absorbing barrier before time T; and the weak convergence of this conditional process as T → ∞. We prove a characterization of convergence in terms of the distribution of the process at some arbitrary positive time, t, introduce a decay parameter for the time to absorption, give an example where weak convergence fails, and give sufficient conditions for weak convergence in terms of the existence of a quasi-stationary limit, and a recurrence property of the original process.

Using an approach similar to that of Guivarc'h and Hardy (1988), we show that the local limit theorem holds for a Markov chain on a countable state space, with non-uniform ergodicity, when the recurrence is fast enough. We present a detailed study of a typical example, the reflected random walk on the positive half-line with negative mean and finite exponential moment. The results can be extended to some random walks on ℕ.

In this paper, bidimensional stochastic processes defined by ax(t) = y(t)dt and dy(t) = m(y)dt + [2v(y)]1/2 dW(t), where W(t) is a standard Brownian motion, are considered. In the first section, results are obtained that allow us to characterize the moment-generating function of first-passage times for processes of this type. In Sections 2 and 5, functions are computed, first by fixing the values of the infinitesimal parameters m(y) and v(y) then by the boundary of the stopping region.

Let X(t) be a non-homogeneous birth and death process. In this paper we develop a general method of estimating bounds for the state probabilities for X(t), based on inequalities for the solutions of the forward Kolmogorov equations. Specific examples covered include simple estimates of Pr(X(t) < j | X(0) = k) for the M(t)/M(t)/N/0 and M(t)/M(t)/N queue-length processes.