We consider iterations of smooth non-invertible maps on manifolds of real dimension 4, which are hyperbolic, conformal on stable manifolds and finite-to-one on basic sets. The dynamics of non-invertible maps can be very different than the one of diffeomorphisms, as was shown for example in [4, 7, 12, 17, 19], etc. In [13] we introduced a notion of inverse topological pressure P− which can be used for estimates of the stable dimension δs(x) (i.e the Hausdorff dimension of the intersection between the local stable manifold Wsr(x) and the basic set Λ, x ∈ Λ). In [10] it is shown that the usual Bowen equation is not always true in the case of non-invertible maps. By using the notion of inverse pressure P−, we showed in [13] that δs(x) ≤ ts(ϵ), where ts(ϵ) is the unique zero of the function t → P−(tφs, ϵ), for φs(y):= log|Dfs(y)|, y ∈ Λ and ϵ > 0 small. In this paper we prove that if Λ is not a repellor, then ts(ϵ) < 2 for any ϵ > 0 small enough. In [11] we showed that a holomorphic s-hyperbolic map on  2
2 has a global unstable set with empty interior. Here we show in a more general setting than in [11], that the Hausdorff dimension of the global unstable set Wu(
has a global unstable set with empty interior. Here we show in a more general setting than in [11], that the Hausdorff dimension of the global unstable set Wu(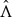 ) is strictly less than 4 under some technical derivative condition. In the non-invertible case we may have (infinitely) many unstable manifolds going through a point in Λ, and the number of preimages belonging to Λ may vary. In [17], Qian and Zhang studied the case of attractors for non-invertible maps and gave a condition for a basic set to be an attractor in terms of the pressure of the unstable potential. In our case the situation is different, since the local unstable manifolds may intersect both inside and outside Λ and they do not form a foliation like the stable manifolds. We prove here that the upper box dimension of Wsr(x) ∩ Λ is less than ts(ϵ) for any point x ∈ Λ. We give then an estimate of the Hausdorff dimension of Wu(
) is strictly less than 4 under some technical derivative condition. In the non-invertible case we may have (infinitely) many unstable manifolds going through a point in Λ, and the number of preimages belonging to Λ may vary. In [17], Qian and Zhang studied the case of attractors for non-invertible maps and gave a condition for a basic set to be an attractor in terms of the pressure of the unstable potential. In our case the situation is different, since the local unstable manifolds may intersect both inside and outside Λ and they do not form a foliation like the stable manifolds. We prove here that the upper box dimension of Wsr(x) ∩ Λ is less than ts(ϵ) for any point x ∈ Λ. We give then an estimate of the Hausdorff dimension of Wu(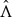 ) by a different technique, using the Holder continuity of the unstable manifolds with respect to their prehistories.
) by a different technique, using the Holder continuity of the unstable manifolds with respect to their prehistories.