In this paper we carry out a linear stability analysis within the Stokes layer that, under suitable conditions, forms at the surface of a circular cylinder in periodic orbital motion. The analysis is related to that performed by Seminara [1,2] in the Stokes layer on a torsionally oscillating cylinder and by Hall [3] in the Stokes layer at the surface of a cylinder in purely oscillatory motion. In all cases we find that the minimum critical Taylor number is located where the flow at the edge of the Stokes layer has maximum speed in each period of the motion.

Let (Sn)n = 1,2,… be the strictly increasing sequence of those natural numbers that can be represented as the sum of three cubes of positive integers. The estimate

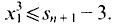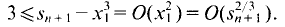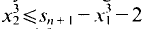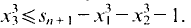is easily proved as follows: Let x1 be the largest natural number with Then This procedure is iterated by choosing x2 and then x3 as the largest natural numbers satisfying and Thus 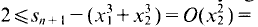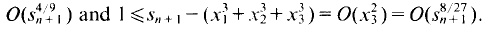Since 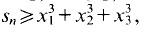this implies (1).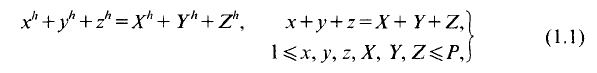

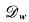A particular solution to the biharmonic equation is described which represents a slow viscous flow near a sharp edge. It shows separation streamlines which are tangential to the plate at the edge, when the dominant behaviour there is a combination of the flow around the edge (which provides zero vorticity on the plate) plus a simple linear shear.

In this paper we investigate the solutions in integers x, y, z, X, Y, Z of the system

where P is a real number that may be taken to be arbitrarily large, and the (fixed) integer exponent h satisfies h≥4. The system has 6P3 + O(P2) “trivial” solutions in which x, y, z are a permutation of X, Y, Z. Our result implies that the number of non-trivial solutions is at most o(P3), so that the total number of solutions is asymptotic to 6P3.

For a fixed integer k ≥ 2 suppose we have functions Li (x) satisfying the following conditions.

Let ν be a valuation of any rank of a field K with value group Gν and f(X)= Xm + alXm−1 + … + am be a polynomial over K. In this paper, it is shown that if (ν(ai)/i)≥(ν(am)/m)>0 for l≤i≤m, and there does not exist any integer r>1 dividing m such that ν(am)/r∈Gν, then f(X) is irreducible over K. It is derived as a special case of a more general result proved here. It generalizes the usual Eisenstein Irreducibility Criterion and an Irreducibility Criterion due to Popescu and Zaharescu for discrete, rank-1 valued fields, (cf. [Journal of Number Theory, 52 (1995), 98–118]).

Let W denote a positive, increasing and continuous function on [1, ∞]. We write to denote the Dirichlettype space of functions 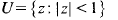f that are holomorphic in the unit disc and for which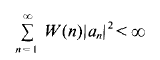

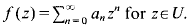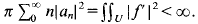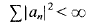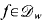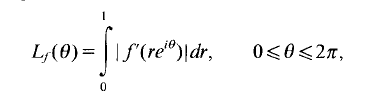
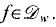
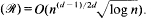Where If W(x) = x for all x, then is the classicial Dirichlet space for which Note also that for every so, by Fatu's theoreum, every function in . ha finite radial(and angular) limits a.e. on the boundary of U. The question of the existence a.e. on ∂U of certain tangential limits for functions in has been considered in [6,11], but we shall be concerned here with the radial variation

i.e., the length of the image of the ray from 0 to eiθ under the mapping w = f(z), and, in particular, with the size of the set of values of θ for which Lf(θ) can be infinite when

Recently, it has been shown that tight or almost tight upper bounds for the discrepancy of many geometrically denned set systems can be derived from simple combinatorial parameters of these set systems. Namely, if the primal shatter function of a set system ℛ on an n-point set X is bounded by const. md, then the discrepancy disc (ℛ) = O(n(d−1)/2d) (which is known to be tight), and if the dual shatter function is bounded by const. 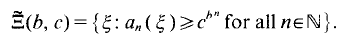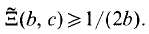md, then disc We prove that for d = 2, 3, the latter bound also cannot be improved in general. We also show that bounds on the shatter functions alone do not imply the average (L1)-discrepancy to be much smaller than the maximum discrepancy: this contrasts results of Beck and Chen for certain geometric cases. In the proof we give a construction of a certain asymptotically extremal bipartite graph, which may be of independent interest.

Let [0;a1(ξ), a2(ξ),…] denote the continued fraction expansion of ξ∈[0, 1]. The problem of estimating the fractional dimension of sets of continued fractions emerged in late twenties in papers by Jarnik [6, 7] and Besicovitch [1] and since then has been addressed by a number of authors (see [2, 4, 5, 8, 9]). In particular, Good [4] proved that the set of all ξ, for which an(ξ)→∞ as n→∞ has the Hausdorff dimension ½ For the set of continued fractions whose expansion terms tend to infinity doubly exponentially the dimension decreases even further. More precisely, let

Hirst [5] showed that dim On the other hand, Moorthy [8] showed that dim 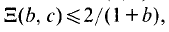where

Ramanujan's work on the asymptotic behaviour of the hypergeometric function has been recently refined to the zero-balanced Gaussian hypergeometric function F(a, b; a + b; x) as x→1.We extend these results for F(a, b; c; x) when a, b, c>0 and c<a + b.

It is known that if A and B are nontriangular 2 × 2 non-negative integral matrices similar over the integers and –tr A ≤det A, then A and B are strongly shift equivalent. Suppose that A and B are 2 × 2 non-negative integral matrices similar over the integers. In this article it is shown that if –2 tr A≤det A <– tr A and if | det A | is not a prime, then A and B are strongly shift equivalent.

In this note we point out that a simple proof of the lower bound of the sets (b, c), and so also of Ξ(b, c), defined in the previous paper [1] can be obtained as a simple application of a general method. By Example 4.6 from [2], if [0, 1] = E0⊃E1⊃ … are sets each of which is a finite union of disjoint closed intervals such that each interval of Ek−1, contains at least mk intervals of Ek which are separated by gaps of lengths at least εk, and if mk≥2 and εk≥εk+1>0, then the dimension of the intersection of Ek is at least

We show that a measure on ℝd is linearly rectifiable if, and only if, the lower l-density is positive and finite and agrees with the lower average l-density almost everywhere.

Call a set of natural numbers subset-sum-distinct (or SSD) if all pairwise distinct subsets have unequal sums. One wants to construct SSD sets in which the largest element is as small as possible. Given any SSD set, it is easy to construct an SSD set with one more element in which the biggest element is exactly double the biggest element in the original set. For any SSD set, we construct another SSD set with k more elements whose largest element is less than 2k times the largest element in the original set. This claim has been made previously for a different construction, but we show that that claim is false.

We provide a unified and simplified proof that for any partition of (0, 1] into sets that are measurable or have the property of Baire, one cell will contain an infinite sequence together with all of its sums (finite or infinite) without repetition. In fact any set which is large around 0 in the sense of measure or category will contain such a sequence. We show that sets with 0 as a density point have very rich structure. 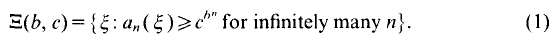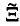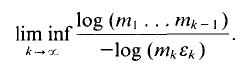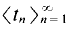Call a sequence and its resulting all-sums set 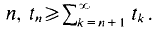structured provided for each We show further that structured all-sums sets with positive measure are not partition regular even if one allows shifted all-sums sets. That is, we produce a two cell measurable partition of (0, 1 ] such that neither set contains a translate of any structured all-sums set with positive measure.

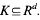A random polytope, Kn, is the convex hull of n points chosen randomly, independently, and uniformly from a convex body It is shown here that, with high probability, Kn can be obtained by taking the convex hull of m = o(n) points chosen independently and uniformly from a small neighbourhood of the boundary of K.

The forms under discussion are integral positive definite quadratic forms in three variables. Such a form g is called regular if g represents every integer represented by the genus of g. This can be recast in elementary terms: g is regular if the solvability of g≡a (mod n) for every n implies the solvability of g = a.

In what follows, R will denote a commutative domain with 1, and Q(≠R) its field of quotients, which is viewed here as an R-module. By RP we denote the localization of R at the maximal ideal P, and more generally, by MP = Rp⊗RM the localization of the R-module M at P, which we define to be the P-component of M. The symbol R* will mean the multiplicative monoid of nonzero elements of R. For a submonoid S of R*, Rs will denote the localization of R at S.

Decompositions of simply connected 4-manifolds into three closed 4-balls are studied from the view-point of abstract regular polytopes of Schläfli type {p, q, 2, 3}. The three balls correspond to three ditopes, their common intersection corresponds to a regular map of type {p, q} as an equilibrium surface whose genus equals the “genus” of the 4-manifold.

In [CKR], Chan, Kim and Raghavan determine all universal positive ternary integral quadratic forms over real quadratic number fields. In this context, universal means that the form represents all totally positive elements of the ring of integers of the underlying field. This generalizes the usage of the term introduced by Dickson for the case of the ring of rational integers [D]. In the present paper, we will continue the investigation of quadratic forms with this property, considering positive quaternary forms over totally real number fields. The main goal of the paper is to prove that if E is a totally real number field of odd degree over the field of rational numbers, then there are at most finitely many inequivalent universal positive quaternary quadratic forms over the ring of integers of E. In fact, the stronger result will be proved that this finiteness holds for those forms which represent all totally positive multiples of any fixed totally positive integer. The necessity of the assumption of oddness of the degree of the extension for a general result of this type can be seen from the existence of universal ternary forms over certain real quadratic fields (for example, the sum of three squares over the field ℚ(√5), as first shown by Maass [M]).