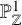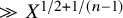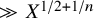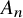1 Introduction
In the first article [Reference Bhargava, Shankar and Wang11] of this two-part series, we proved that when monic integer polynomials
![]() $f(x)=x^n+a_1x^{n-1}+\cdots +a_n$
of fixed degree n are ordered by
$f(x)=x^n+a_1x^{n-1}+\cdots +a_n$
of fixed degree n are ordered by
![]() $\mathrm {{max}}\{|a_1|,\ldots ,|a_n|^{1/n}\}$
, a positive proportion have squarefree discriminant. The purpose of this article is to prove the analogous result for integral binary n-ic forms.
$\mathrm {{max}}\{|a_1|,\ldots ,|a_n|^{1/n}\}$
, a positive proportion have squarefree discriminant. The purpose of this article is to prove the analogous result for integral binary n-ic forms.
Recall that the discriminant
![]() $\Delta (f)$
of a binary n-ic form over a field K is a homogeneous polynomial of degree
$\Delta (f)$
of a binary n-ic form over a field K is a homogeneous polynomial of degree
![]() $2n-2$
in the coefficients of f, whose nonvanishing is equivalent to f having n distinct linear factors over an algebraic closure
$2n-2$
in the coefficients of f, whose nonvanishing is equivalent to f having n distinct linear factors over an algebraic closure
![]() $\overline {K}$
of K. We order integral binary n-ic forms
$\overline {K}$
of K. We order integral binary n-ic forms
![]() $f(x,y)=a_0x^n+a_1x^{n-1}y+\cdots +a_ny^n$
by their height
$f(x,y)=a_0x^n+a_1x^{n-1}y+\cdots +a_ny^n$
by their height
![]() $H(f)$
given by
$H(f)$
given by
![]() $H(f):= \mathrm {{max}}\{|a_0|,\ldots ,|a_n|\},$
(i.e., the maximum of the absolute values of the coefficients). Then a natural question is as follows: When ordered by height, what is the density of integral binary n-ic forms whose discriminant is squarefree? For
$H(f):= \mathrm {{max}}\{|a_0|,\ldots ,|a_n|\},$
(i.e., the maximum of the absolute values of the coefficients). Then a natural question is as follows: When ordered by height, what is the density of integral binary n-ic forms whose discriminant is squarefree? For
![]() $n=2$
, classical methods in sieve theory yield the answer. For
$n=2$
, classical methods in sieve theory yield the answer. For
![]() $n=3$
and
$n=3$
and
![]() $n=4$
, results of Davenport–Heilbronn [Reference Davenport and Heilbronn15] and the first and second authors [Reference Bhargava and Shankar10], respectively, answer the question in the related setting in which we consider
$n=4$
, results of Davenport–Heilbronn [Reference Davenport and Heilbronn15] and the first and second authors [Reference Bhargava and Shankar10], respectively, answer the question in the related setting in which we consider
![]() $\mathrm {{GL}}_2({\mathbb {Z}})$
-orbits on binary n-ic forms. However, for
$\mathrm {{GL}}_2({\mathbb {Z}})$
-orbits on binary n-ic forms. However, for
![]() $n\geq 5$
, it has not previously been known whether this density exists or even whether the lower density is positive. In this paper, we prove the following:
$n\geq 5$
, it has not previously been known whether this density exists or even whether the lower density is positive. In this paper, we prove the following:
Theorem 1. Let
![]() $n\geq 2$
be an integer. When integral binary n-ic forms
$n\geq 2$
be an integer. When integral binary n-ic forms
![]() $f(x,y)=a_0x^n+a_1x^{n-1}y+\cdots +a_n y^n$
are ordered by
$f(x,y)=a_0x^n+a_1x^{n-1}y+\cdots +a_n y^n$
are ordered by
![]() $H(f):=\mathrm {{max}}\{|a_0|,\ldots ,|a_n|\}. $
, the density of forms having squarefree discriminant exists and is equal to
$H(f):=\mathrm {{max}}\{|a_0|,\ldots ,|a_n|\}. $
, the density of forms having squarefree discriminant exists and is equal to
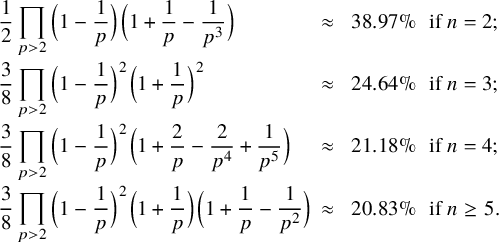 $$ \begin{align*} \begin{array}{lll} \displaystyle\frac{1}{2} \prod_{p>2}\Big(1-\frac{1}{p}\Big) \Big(1+\frac{1}{p}-\frac{1}{p^3}\Big) &\approx \;\;38.97\%&\text{ if }n=2; \\[.175in] \displaystyle\frac{3}{8} \prod_{p>2}\Big(1-\frac{1}{p}\Big)^2\Big(1+\frac{1}{p}\Big)^2&\approx \;\;24.64\% &\text{ if }n=3; \\[.175in] \displaystyle\frac{3}{8} \prod_{p>2}\Big(1-\frac{1}{p}\Big)^2 \Big(1+\frac{2}{p}-\frac{2}{p^4}+\frac{1}{p^5}\Big)&\approx\;\;21.18\% &\text{ if }n=4; \\[.175in] \displaystyle\frac{3}{8} \prod_{p>2}\Big(1-\frac{1}{p}\Big)^2 \Big(1+\frac{1}{p}\Big)\Big(1+\frac{1}{p}-\frac{1}{p^2}\Big)&\approx \;\;20.83\% &\text{ if }n\geq5. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{lll} \displaystyle\frac{1}{2} \prod_{p>2}\Big(1-\frac{1}{p}\Big) \Big(1+\frac{1}{p}-\frac{1}{p^3}\Big) &\approx \;\;38.97\%&\text{ if }n=2; \\[.175in] \displaystyle\frac{3}{8} \prod_{p>2}\Big(1-\frac{1}{p}\Big)^2\Big(1+\frac{1}{p}\Big)^2&\approx \;\;24.64\% &\text{ if }n=3; \\[.175in] \displaystyle\frac{3}{8} \prod_{p>2}\Big(1-\frac{1}{p}\Big)^2 \Big(1+\frac{2}{p}-\frac{2}{p^4}+\frac{1}{p^5}\Big)&\approx\;\;21.18\% &\text{ if }n=4; \\[.175in] \displaystyle\frac{3}{8} \prod_{p>2}\Big(1-\frac{1}{p}\Big)^2 \Big(1+\frac{1}{p}\Big)\Big(1+\frac{1}{p}-\frac{1}{p^2}\Big)&\approx \;\;20.83\% &\text{ if }n\geq5. \end{array} \end{align*} $$
To any nonzero integral binary n-ic form
![]() $f(x,y) = a_0x^n + \cdots + a_ny^n$
, we may naturally attach a rank-n ring
$f(x,y) = a_0x^n + \cdots + a_ny^n$
, we may naturally attach a rank-n ring
![]() $R_f$
(see Birch–Merriman [Reference Birch and Merriman12], Nakagawa [Reference Nakagawa24] and Wood [Reference Wood38]), defined as follows when
$R_f$
(see Birch–Merriman [Reference Birch and Merriman12], Nakagawa [Reference Nakagawa24] and Wood [Reference Wood38]), defined as follows when
![]() $a_0\neq 0$
. Let
$a_0\neq 0$
. Let
![]() $\theta $
denote the image of x in
$\theta $
denote the image of x in
![]() $K_f:={\mathbb {Q}}[x]/(f(x,1))$
. Let
$K_f:={\mathbb {Q}}[x]/(f(x,1))$
. Let
![]() $R_f$
be the free rank-
$R_f$
be the free rank-
![]() $n {\mathbb {Z}}$
-submodule of
$n {\mathbb {Z}}$
-submodule of
![]() $K_f$
generated by
$K_f$
generated by
![]() $1, \,a_0\theta , \,a_0\theta ^2+a_1\theta ,\,\ldots ,\,a_0\theta ^{n-1}+\cdots +a_{n-1}\theta $
. Then
$1, \,a_0\theta , \,a_0\theta ^2+a_1\theta ,\,\ldots ,\,a_0\theta ^{n-1}+\cdots +a_{n-1}\theta $
. Then
![]() $R_f$
is in fact closed under multiplication and forms a ring whose discriminant is equal to the discriminant of
$R_f$
is in fact closed under multiplication and forms a ring whose discriminant is equal to the discriminant of
![]() $f(x)$
. Our next result determines the density of irreducible integral binary forms f for which
$f(x)$
. Our next result determines the density of irreducible integral binary forms f for which
![]() $R_f$
is the maximal order in its field of fractions.
$R_f$
is the maximal order in its field of fractions.
Theorem 2. Let
![]() $n\geq 2$
be an integer. When irreducible integral binary n-ic forms
$n\geq 2$
be an integer. When irreducible integral binary n-ic forms
![]() $f(x,y)=a_0x^n+a_1x^{n-1}y+\cdots +a_ny^n$
are ordered by
$f(x,y)=a_0x^n+a_1x^{n-1}y+\cdots +a_ny^n$
are ordered by
![]() $H(f):=\mathrm {{max}}\{|a_0|,\ldots ,|a_n|\}$
, the density of forms f such that
$H(f):=\mathrm {{max}}\{|a_0|,\ldots ,|a_n|\}$
, the density of forms f such that
![]() $R_f$
is the ring of integers in its field of fractions exists and is equal to
$R_f$
is the ring of integers in its field of fractions exists and is equal to
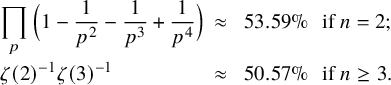 $$ \begin{align*} \begin{array}{lll} \displaystyle\prod_p \Big(1-\frac{1}{p^2}-\frac{1}{p^3}+\frac{1}{p^4}\Big) &\approx \;\;53.59\%&\text{ if }n=2;\\[.1725in] \displaystyle\zeta(2)^{-1}\zeta(3)^{-1} &\approx \;\;50.57\%&\text{ if }n\geq3.\end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{lll} \displaystyle\prod_p \Big(1-\frac{1}{p^2}-\frac{1}{p^3}+\frac{1}{p^4}\Big) &\approx \;\;53.59\%&\text{ if }n=2;\\[.1725in] \displaystyle\zeta(2)^{-1}\zeta(3)^{-1} &\approx \;\;50.57\%&\text{ if }n\geq3.\end{array} \end{align*} $$
In particular, Theorem 2 yields the first unconditional Bertini theorem for arithmetic schemes of dimension
![]() $\geq 2$
as conjectured by Poonen [Reference Poonen28, §5]. Indeed, for a quasiprojective subscheme X of
$\geq 2$
as conjectured by Poonen [Reference Poonen28, §5]. Indeed, for a quasiprojective subscheme X of
![]() ${\mathbb {P}}^n_{\mathbb {Z}}$
that is regular of dimension m, Poonen conjectured that the density of hyperplane sections of X that are regular of dimension
${\mathbb {P}}^n_{\mathbb {Z}}$
that is regular of dimension m, Poonen conjectured that the density of hyperplane sections of X that are regular of dimension
![]() $m-1$
should equal
$m-1$
should equal
![]() $\zeta _X(m+1)$
, where
$\zeta _X(m+1)$
, where
![]() $\zeta _X$
denotes the zeta function of X. Since the subscheme of
$\zeta _X$
denotes the zeta function of X. Since the subscheme of
![]() ${\mathbb {P}}^1_{\mathbb {Z}}$
cut out by an integral binary n-ic form f is regular if and only if
${\mathbb {P}}^1_{\mathbb {Z}}$
cut out by an integral binary n-ic form f is regular if and only if
![]() $R_f$
is maximal, and the zeta function of
$R_f$
is maximal, and the zeta function of
![]() ${\mathbb {P}}^1_{\mathbb {Z}}$
is given by
${\mathbb {P}}^1_{\mathbb {Z}}$
is given by
![]() $\zeta _{{\mathbb {P}}^1_{\mathbb {Z}}}(s)=\zeta (s)\zeta (s-1)$
, we have
$\zeta _{{\mathbb {P}}^1_{\mathbb {Z}}}(s)=\zeta (s)\zeta (s-1)$
, we have
![]() $\zeta _{{\mathbb {P}}^1_{\mathbb {Z}}}(\dim ({\mathbb {P}}^1_{\mathbb {Z}})+1)^{-1}=\zeta (2)^{-1}\zeta (3)^{-1}$
. Therefore, Theorem 2 yields an unconditional proof of [Reference Poonen28, Theorem 5.1] for the case
$\zeta _{{\mathbb {P}}^1_{\mathbb {Z}}}(\dim ({\mathbb {P}}^1_{\mathbb {Z}})+1)^{-1}=\zeta (2)^{-1}\zeta (3)^{-1}$
. Therefore, Theorem 2 yields an unconditional proof of [Reference Poonen28, Theorem 5.1] for the case
![]() $X={\mathbb {P}}^1_{\mathbb {Z}}$
with the usual ‘box ordering’ on the forms defining the hyperplane sections. In fact, we prove the stronger result that for every fixed
$X={\mathbb {P}}^1_{\mathbb {Z}}$
with the usual ‘box ordering’ on the forms defining the hyperplane sections. In fact, we prove the stronger result that for every fixed
![]() $n\geq 3$
, the density of regular binary n-ic forms is
$n\geq 3$
, the density of regular binary n-ic forms is
![]() $\zeta (2)^{-1}\zeta (3)^{-1}$
, while arithmetic Bertini only claims this in the limit as
$\zeta (2)^{-1}\zeta (3)^{-1}$
, while arithmetic Bertini only claims this in the limit as
![]() $n\to \infty $
.
$n\to \infty $
.
As a further application of our methods, we obtain the following theorem:
Theorem 3. For each
![]() $n\geq 3$
, the number of isomorphism classes of number fields of degree n with associated Galois group
$n\geq 3$
, the number of isomorphism classes of number fields of degree n with associated Galois group
![]() $S_n$
and absolute discriminant less than X is
$S_n$
and absolute discriminant less than X is
![]() $\gg X^{1/2+1/(n-1)}$
.
$\gg X^{1/2+1/(n-1)}$
.
Our lower bound in Theorem 3 on the number of degree-
![]() $n S_n$
-number fields of absolute discriminant less than X improves the previous best-known lower bound of
$n S_n$
-number fields of absolute discriminant less than X improves the previous best-known lower bound of
![]() $X^{1/2+1/n}$
obtained in [Reference Bhargava, Shankar and Wang11]. We note that the number fields constructed in Theorem 3 can all be taken to have squarefree discriminant.
$X^{1/2+1/n}$
obtained in [Reference Bhargava, Shankar and Wang11]. We note that the number fields constructed in Theorem 3 can all be taken to have squarefree discriminant.
Our results also correct an error in, and thus resurrect, all the results of Nakagawa [Reference Nakagawa24] and [Reference Nakagawa26] that had been subsequently retracted in [Reference Nakagawa25] and [Reference Nakagawa27]. Specifically, the retracted theorems [Reference Nakagawa24, Theorems 3–4] and [Reference Nakagawa26, Theorem 2] regarding binary forms and
![]() $A_n$
-extensions of quadratic fields can now be taken to be true. In particular, we obtain the following:
$A_n$
-extensions of quadratic fields can now be taken to be true. In particular, we obtain the following:
Theorem 4. For
![]() $n\geq 3$
, the total number of unramified
$n\geq 3$
, the total number of unramified
![]() $A_n$
-extensions of real
$A_n$
-extensions of real
![]() $($
resp., imaginary
$($
resp., imaginary
![]() $)$
quadratic fields F, across all such F such that
$)$
quadratic fields F, across all such F such that
![]() $|\mathrm {{Disc}}(F)|<X$
, is
$|\mathrm {{Disc}}(F)|<X$
, is
![]() $\gg X^{(n+1)/(2n-2)}$
.
$\gg X^{(n+1)/(2n-2)}$
.
Theorem 4 yields the best-known lower bounds on the number of unramified
![]() $A_n$
-extensions of quadratic fields when
$A_n$
-extensions of quadratic fields when
![]() $n>5$
. For improved bounds in the cases
$n>5$
. For improved bounds in the cases
![]() $n\leq 5$
, see [Reference Bhargava4, Theorem 1.4]. For the best-known bounds on the number of quadratic fields of bounded discriminant admitting an unramified
$n\leq 5$
, see [Reference Bhargava4, Theorem 1.4]. For the best-known bounds on the number of quadratic fields of bounded discriminant admitting an unramified
![]() $A_n$
-extension, see Kedlaya [Reference Kedlaya21, Corollary 1.4]. Other related works include Uchida [Reference Uchida37], Yamamoto [Reference Yamamoto40] and Yamamura [Reference Yamamura41].
$A_n$
-extension, see Kedlaya [Reference Kedlaya21, Corollary 1.4]. Other related works include Uchida [Reference Uchida37], Yamamoto [Reference Yamamoto40] and Yamamura [Reference Yamamura41].
The main technical ingredient required to prove all the above results is a ‘tail estimate’ which shows that not too many discriminants of integral binary n-ic forms f are divisible by
![]() $p^2$
when p is large relative to the discriminant of f (here, large means larger than
$p^2$
when p is large relative to the discriminant of f (here, large means larger than
![]() $H(f)$
, say). It is these tail estimates that were missing in Nakagawa’s work. For a prime p, and an integral binary n-ic form f such that
$H(f)$
, say). It is these tail estimates that were missing in Nakagawa’s work. For a prime p, and an integral binary n-ic form f such that
![]() $p^2\mid \Delta (f)$
, we say that
$p^2\mid \Delta (f)$
, we say that
![]() $p^2$
strongly divides
$p^2$
strongly divides
![]() $\Delta (f)$
if
$\Delta (f)$
if
![]() $p^2\mid \Delta (f + pg)$
for every integral binary n-ic form g; otherwise, we say
$p^2\mid \Delta (f + pg)$
for every integral binary n-ic form g; otherwise, we say
![]() $p^2$
weakly divides
$p^2$
weakly divides
![]() $\Delta (f)$
. For any squarefree integer
$\Delta (f)$
. For any squarefree integer
![]() $m>0$
, let
$m>0$
, let
![]() ${\mathcal {W}}_m^{\mathrm {{{(1)}}}}$
(resp.,
${\mathcal {W}}_m^{\mathrm {{{(1)}}}}$
(resp.,
![]() ${\mathcal {W}}_m^{\mathrm {{{(2)}}}}$
) denote the set of integral binary n-ic forms whose discriminants are strongly divisible (resp., weakly divisible) by
${\mathcal {W}}_m^{\mathrm {{{(2)}}}}$
) denote the set of integral binary n-ic forms whose discriminants are strongly divisible (resp., weakly divisible) by
![]() $p^2$
for every prime factor p of m.
$p^2$
for every prime factor p of m.
We prove the following tail estimates:
Theorem 5. For an integer
![]() $n\geq 3$
, a positive real number M and any
$n\geq 3$
, a positive real number M and any
![]() $\epsilon>0$
, we have
$\epsilon>0$
, we have
 $$ \begin{align*} &\mathrm{(a) }\ \#\bigcup_{\substack{m>M\\ m\;\mathrm{ squarefree}}} \{f\in{\mathcal{W}}_m^{\mathrm{{{(1)}}}}:H(f)<X\} = O_\epsilon\Big(\frac{X^{n+1+\epsilon}}{M}+X^{n}\Big); \\&\mathrm{(b) }\ \#\bigcup_{\substack{m>M\\ m\;\mathrm{ squarefree} }}\{f\in{\mathcal{W}}_m^{\mathrm{{(2)}}}:H(f)<X\} = O_\epsilon\Big(\frac{X^{n+1+\epsilon}}{M}+X^{n+1-1/(2n)+\epsilon}\Big),\text{ if }2\nmid n; \\&\mathrm{(c) } \ \#\bigcup_{\substack{m>M\\ m\;\mathrm{ squarefree} }}\{f\in{\mathcal{W}}_m^{\mathrm{{(2)}}}:H(f)<X\} = O\Big(\frac{X^{n+1+1/(88n^5)}}{\sqrt{M}}+X^{n+1-1/(88n^6)}\Big),\text{ if }2\mid n. \end{align*} $$
$$ \begin{align*} &\mathrm{(a) }\ \#\bigcup_{\substack{m>M\\ m\;\mathrm{ squarefree}}} \{f\in{\mathcal{W}}_m^{\mathrm{{{(1)}}}}:H(f)<X\} = O_\epsilon\Big(\frac{X^{n+1+\epsilon}}{M}+X^{n}\Big); \\&\mathrm{(b) }\ \#\bigcup_{\substack{m>M\\ m\;\mathrm{ squarefree} }}\{f\in{\mathcal{W}}_m^{\mathrm{{(2)}}}:H(f)<X\} = O_\epsilon\Big(\frac{X^{n+1+\epsilon}}{M}+X^{n+1-1/(2n)+\epsilon}\Big),\text{ if }2\nmid n; \\&\mathrm{(c) } \ \#\bigcup_{\substack{m>M\\ m\;\mathrm{ squarefree} }}\{f\in{\mathcal{W}}_m^{\mathrm{{(2)}}}:H(f)<X\} = O\Big(\frac{X^{n+1+1/(88n^5)}}{\sqrt{M}}+X^{n+1-1/(88n^6)}\Big),\text{ if }2\mid n. \end{align*} $$
The estimate in the strongly divisible Case (a) of Theorem 5 follows from geometric techniques – namely, the quantitative version of the Ekedahl geometric sieve as developed by the first author [Reference Bhargava4]. The estimates in the weakly divisible Cases (b) and (c) of Theorem 5 are considerably more difficult (particularly (c)), and we describe their proofs in the next section. Our tail estimate, in fact, allows us to prove Theorems 1 and 2 with power-saving error terms:
Theorem 6. Let
![]() $V_n=\mathrm {{Sym}}^n(2)$
denote the space of binary n-ic forms. Define
$V_n=\mathrm {{Sym}}^n(2)$
denote the space of binary n-ic forms. Define
![]() $\eta _n$
to be
$\eta _n$
to be
![]() $1/(2n)$
when n is odd and
$1/(2n)$
when n is odd and
![]() $1/(88n^6)$
when n is even. Then
$1/(88n^6)$
when n is even. Then
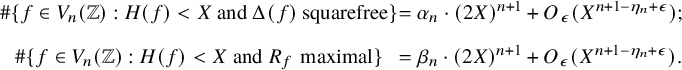 $$ \begin{align*} \begin{array}{ccl} \#\{f\in V_n({\mathbb{Z}}) : H(f)<X \text{ and } \Delta(f)\text{ squarefree}\}&\!\!=\!\!& \alpha_n\cdot (2X)^{n+1} + O_\epsilon(X^{n+1-\eta_n+\epsilon});\\[.125in] \#\{f\in V_n({\mathbb{Z}}) : H(f)<X \text{ and }R_f\text{ maximal}\}&\!\!=\!\!& \beta_n\cdot (2X)^{n+1} + O_\epsilon(X^{n+1-\eta_n+\epsilon}). \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{ccl} \#\{f\in V_n({\mathbb{Z}}) : H(f)<X \text{ and } \Delta(f)\text{ squarefree}\}&\!\!=\!\!& \alpha_n\cdot (2X)^{n+1} + O_\epsilon(X^{n+1-\eta_n+\epsilon});\\[.125in] \#\{f\in V_n({\mathbb{Z}}) : H(f)<X \text{ and }R_f\text{ maximal}\}&\!\!=\!\!& \beta_n\cdot (2X)^{n+1} + O_\epsilon(X^{n+1-\eta_n+\epsilon}). \end{array} \end{align*} $$
These power saving bounds have applications towards level-of-distribution questions when counting integral binary n-ic forms f of bounded height with
![]() $\Delta (f)$
squarefree (resp.,
$\Delta (f)$
squarefree (resp.,
![]() $R_f$
maximal) satisfying splitting conditions at finitely many primes. Such level-of-distribution results in turn have applications towards a host of problems in analytic number theory, such as studying statistics of Artin L-functions attached to binary n-ic forms and proving lower bounds on the number of degree-n number fields which are ramified only at a bounded number of primes, among many others. For examples of such applications of level-of-distribution results, see, for example, [Reference Belabas and Fouvry1, Reference Cho and Kim13, Reference Shankar, Södergren and Templier33, Reference Shankar, Södergren and Templier34, Reference Taniguchi and Thorne36].
$R_f$
maximal) satisfying splitting conditions at finitely many primes. Such level-of-distribution results in turn have applications towards a host of problems in analytic number theory, such as studying statistics of Artin L-functions attached to binary n-ic forms and proving lower bounds on the number of degree-n number fields which are ramified only at a bounded number of primes, among many others. For examples of such applications of level-of-distribution results, see, for example, [Reference Belabas and Fouvry1, Reference Cho and Kim13, Reference Shankar, Södergren and Templier33, Reference Shankar, Södergren and Templier34, Reference Taniguchi and Thorne36].
We remark that our methods imply that the analogues of all of the above results also hold when local conditions are imposed at finitely many places (including at infinity); the orders of magnitudes in these theorems remain the same, provided that no local conditions are imposed that force the sets being counted in Theorems 1 and 2 to be empty.
Finally, the methods introduced in [Reference Bhargava, Shankar and Wang11] and in the current article have applications beyond just squarefree values of polynomial discriminants. They have been recently adapted in [Reference Bhargava and Ho9] to determine the density of squarefree discriminants of elliptic curves over
![]() ${\mathbb {Q}}$
having two marked rational points. Other applications include determining the density of conductors in some families of elliptic curves [Reference Shankar, Shankar and Wang32] and the density of squarefree values taken by
${\mathbb {Q}}$
having two marked rational points. Other applications include determining the density of conductors in some families of elliptic curves [Reference Shankar, Shankar and Wang32] and the density of squarefree values taken by
![]() $a^4+b^3$
[Reference Sanjaya and Wang29].
$a^4+b^3$
[Reference Sanjaya and Wang29].
2 Outline of proof
As mentioned in the introduction, the uniformity estimate in Theorem 5 is the key to deducing Theorems 1, 2 and 6 via a squarefree sieve. Case (a) of Theorem 5 follows directly from the results in [Reference Bhargava4]. Case (b), which pertains to odd degrees n, can be proven using methods similar to those developed in our previous work [Reference Bhargava, Shankar and Wang11]. However, these methods fail to work for Case (c), which pertains to even degrees n, and a number of new ideas are required to handle this case. It is the proof of this case to which the bulk of our paper is devoted; it requires, in particular, the introduction of a new technique in the geometry of numbers – namely, the techniques of Eskin–Katznelson [Reference Eskin and Katznelson17] used in counting singular symmetric matrices. We believe that this combining of methods may also be useful in other contexts.
In this section, we give a detailed outline of the proof of Case (b) pertaining to odd n. We then explain why this strategy breaks down (quite spectacularly!) when n is even, and finally we describe the new techniques required to complete the proof of Theorem 5(c).
Sketch of the proof of the tail estimate for odd n
Our proof of Theorem 5(b) makes use of the representation of
![]() $G=\mathrm {{SL}}_n$
on the space
$G=\mathrm {{SL}}_n$
on the space
![]() $W=2\otimes \mathrm {{Sym}}_2(n)$
of pairs
$W=2\otimes \mathrm {{Sym}}_2(n)$
of pairs
![]() $(A,B)$
of symmetric
$(A,B)$
of symmetric
![]() $n\times n$
matrices, studied in detail in [Reference Wood39, Reference Bhargava5, Reference Bhargava, Gross and Wang7, Reference Bhargava, Gross and Wang8]. The group G acts on W via
$n\times n$
matrices, studied in detail in [Reference Wood39, Reference Bhargava5, Reference Bhargava, Gross and Wang7, Reference Bhargava, Gross and Wang8]. The group G acts on W via
![]() $\gamma \cdot (A,B)=(\gamma A\gamma ^t,\gamma B\gamma ^t$
) for
$\gamma \cdot (A,B)=(\gamma A\gamma ^t,\gamma B\gamma ^t$
) for
![]() $\gamma \in G$
and
$\gamma \in G$
and
![]() $(A,B)\in W$
. We define the invariant binary form of an element
$(A,B)\in W$
. We define the invariant binary form of an element
![]() $(A,B)\in W$
by
$(A,B)\in W$
by
Then
![]() $f_{A,B}$
is a binary n-ic form satisfying
$f_{A,B}$
is a binary n-ic form satisfying
![]() $f_{\gamma (A,B)}=f_{A,B}$
. Moreover, the ring of polynomial invariants for the action of G on W is freely generated by the coefficients of the invariant binary form. Define the discriminant
$f_{\gamma (A,B)}=f_{A,B}$
. Moreover, the ring of polynomial invariants for the action of G on W is freely generated by the coefficients of the invariant binary form. Define the discriminant
![]() $\Delta (A,B)$
and height
$\Delta (A,B)$
and height
![]() $H(A,B)$
of an element
$H(A,B)$
of an element
![]() $(A,B)\in W$
by
$(A,B)\in W$
by
![]() $\Delta (A,B)=\Delta (f_{A,B})$
and
$\Delta (A,B)=\Delta (f_{A,B})$
and
![]() $H(A,B)=H(f_{A,B})$
.
$H(A,B)=H(f_{A,B})$
.
The first step of our proof is the construction, for every squarefree integer
![]() $m>0$
, of a map
$m>0$
, of a map
such that
![]() $f_{\sigma _m(f)}(x,y)=f(x,y)$
for every
$f_{\sigma _m(f)}(x,y)=f(x,y)$
for every
![]() $f\in {\mathcal {W}}_m^{\mathrm {{{(2)}}}}$
. In our construction, the image of
$f\in {\mathcal {W}}_m^{\mathrm {{{(2)}}}}$
. In our construction, the image of
![]() $\sigma _m$
, in fact, lies in
$\sigma _m$
, in fact, lies in
![]() $W_0({\mathbb {Z}})$
, where
$W_0({\mathbb {Z}})$
, where
![]() $W_0$
is the subspace of W consisting of pairs of matrices whose top left
$W_0$
is the subspace of W consisting of pairs of matrices whose top left
![]() $g\times g$
blocks are
$g\times g$
blocks are
![]() $0$
, where
$0$
, where
![]() $n=2g+1$
. The action of the group G does not preserve
$n=2g+1$
. The action of the group G does not preserve
![]() $W_0$
, and we take
$W_0$
, and we take
![]() $G_0$
to be the maximal parabolic subgroup of G that does preserve
$G_0$
to be the maximal parabolic subgroup of G that does preserve
![]() $W_0$
. When the discriminant polynomial
$W_0$
. When the discriminant polynomial
![]() $\Delta \in {\mathbb {Z}}[W]$
is restricted to
$\Delta \in {\mathbb {Z}}[W]$
is restricted to
![]() $W_0$
, it is no longer irreducible but rather is divisible by the square of a polynomial
$W_0$
, it is no longer irreducible but rather is divisible by the square of a polynomial
![]() $Q\in {\mathbb {Z}}[W_0]$
. This polynomial Q is a relative invariant for the action of
$Q\in {\mathbb {Z}}[W_0]$
. This polynomial Q is a relative invariant for the action of
![]() $G_0$
on
$G_0$
on
![]() $W_0$
. Its significance is that, by construction of
$W_0$
. Its significance is that, by construction of
![]() $\sigma _m$
, every element in the image of
$\sigma _m$
, every element in the image of
![]() $\sigma _m$
has Q-invariant equal to m. To prove Part (b) of Theorem 5, it therefore suffices to estimate the number of
$\sigma _m$
has Q-invariant equal to m. To prove Part (b) of Theorem 5, it therefore suffices to estimate the number of
![]() $G_0({\mathbb {Z}})$
-orbits on
$G_0({\mathbb {Z}})$
-orbits on
![]() $W_0({\mathbb {Z}})$
having height less than X and Q-invariant greater than M.
$W_0({\mathbb {Z}})$
having height less than X and Q-invariant greater than M.
Bounding the number of these orbits is complicated by the fact that
![]() $G_0$
is not reductive. We are rescued by using the full action of
$G_0$
is not reductive. We are rescued by using the full action of
![]() $G({\mathbb {Z}})$
on
$G({\mathbb {Z}})$
on
![]() $W({\mathbb {Z}})$
. This necessitates expanding the definition of the Q-invariant from
$W({\mathbb {Z}})$
. This necessitates expanding the definition of the Q-invariant from
![]() $W_0({\mathbb {Z}})$
to all ‘distinguished’ elements of
$W_0({\mathbb {Z}})$
to all ‘distinguished’ elements of
![]() $W({\mathbb {Z}})$
. An element
$W({\mathbb {Z}})$
. An element
![]() $(A,B)\in W({\mathbb {Z}})$
is distinguished if A and B have a common isotropic g-dimensional subspace defined over
$(A,B)\in W({\mathbb {Z}})$
is distinguished if A and B have a common isotropic g-dimensional subspace defined over
![]() ${\mathbb {Q}}$
. Thus, every element in
${\mathbb {Q}}$
. Thus, every element in
![]() $W_0({\mathbb {Z}})$
(and thus every element in the image of
$W_0({\mathbb {Z}})$
(and thus every element in the image of
![]() $\sigma _m$
) is distinguished. The Q-invariant, though defined initially on
$\sigma _m$
) is distinguished. The Q-invariant, though defined initially on
![]() $W_0$
, can be extended as a function on the set of all triples
$W_0$
, can be extended as a function on the set of all triples
![]() $(A,B,\Lambda )$
, where
$(A,B,\Lambda )$
, where
![]() $(A,B)\in W({\mathbb {Z}})$
is distinguished, and
$(A,B)\in W({\mathbb {Z}})$
is distinguished, and
![]() $\Lambda $
is a common isotropic subspace of A and B. For all but a negligible number of distinguished elements
$\Lambda $
is a common isotropic subspace of A and B. For all but a negligible number of distinguished elements
![]() $(A,B)\in W({\mathbb {Z}})$
, A and B have exactly one common isotropic subspace
$(A,B)\in W({\mathbb {Z}})$
, A and B have exactly one common isotropic subspace
![]() $\Lambda $
defined over
$\Lambda $
defined over
![]() ${\mathbb {Q}}$
. Thus, we may define a
${\mathbb {Q}}$
. Thus, we may define a
![]() $G({\mathbb {Z}})$
-invariant function Q on the set of distinguished pairs
$G({\mathbb {Z}})$
-invariant function Q on the set of distinguished pairs
![]() $(A,B)\in W({\mathbb {Z}})$
outside a negligible number of them. It then suffices to bound the number of
$(A,B)\in W({\mathbb {Z}})$
outside a negligible number of them. It then suffices to bound the number of
![]() $G({\mathbb {Z}})$
-orbits on distinguished elements in
$G({\mathbb {Z}})$
-orbits on distinguished elements in
![]() $W({\mathbb {Z}})$
having bounded height and large Q-invariant.
$W({\mathbb {Z}})$
having bounded height and large Q-invariant.
To obtain such a bound, we construct fundamental domains for the action of
![]() $G({\mathbb {Z}})$
on elements in
$G({\mathbb {Z}})$
on elements in
![]() $W({\mathbb {R}})$
with height less than X. Such a fundamental domain has a natural partition into three parts that we term the main body, the shallow cusp and the deep cusp. We have little control over the Q-invariants of elements in the main body and the shallow cusp. However, it is known [Reference Ho, Shankar and Varma20, Proposition 4.3] that there are a negligible number of integral elements in the shallow cusp. Meanwhile, distinguished elements occur rarely in the main body, a fact we prove via the large sieve.
$W({\mathbb {R}})$
with height less than X. Such a fundamental domain has a natural partition into three parts that we term the main body, the shallow cusp and the deep cusp. We have little control over the Q-invariants of elements in the main body and the shallow cusp. However, it is known [Reference Ho, Shankar and Varma20, Proposition 4.3] that there are a negligible number of integral elements in the shallow cusp. Meanwhile, distinguished elements occur rarely in the main body, a fact we prove via the large sieve.
Finally, the deep cusp lies in
![]() $W_0$
, where an upper bound for the Q-invariant can be obtained. Imposing the condition that this upper bound is greater than M, and counting the number of such points in the deep cusp using the averaging method of [Reference Bhargava3], gives the desired saving for the number of elements in the deep cusp having Q-invariant larger than M. Combining the estimates for the main body, the shallow cusp and the deep cusp yields Part (b) of Theorem 5.
$W_0$
, where an upper bound for the Q-invariant can be obtained. Imposing the condition that this upper bound is greater than M, and counting the number of such points in the deep cusp using the averaging method of [Reference Bhargava3], gives the desired saving for the number of elements in the deep cusp having Q-invariant larger than M. Combining the estimates for the main body, the shallow cusp and the deep cusp yields Part (b) of Theorem 5.
Sketch of the proof of the tail estimate for even n
With W again denoting the space of pairs of symmetric
![]() $n\times n$
matrices, we may attempt to proceed in the same manner as in the case of odd n, by constructing a map
$n\times n$
matrices, we may attempt to proceed in the same manner as in the case of odd n, by constructing a map
such that
![]() $f_{\sigma _m(f)}(x,y)=f(x,y)$
for every
$f_{\sigma _m(f)}(x,y)=f(x,y)$
for every
![]() $f\in {\mathcal {W}}_m^{\mathrm {{{(2)}}}}$
. However, such a map does not exist in the case that n is even! Indeed, there exist integral binary n-ic forms
$f\in {\mathcal {W}}_m^{\mathrm {{{(2)}}}}$
. However, such a map does not exist in the case that n is even! Indeed, there exist integral binary n-ic forms
![]() $f(x,y)$
that cannot be expressed as
$f(x,y)$
that cannot be expressed as
![]() $\det (Ax - By)$
– even up to sign – for any integral
$\det (Ax - By)$
– even up to sign – for any integral
![]() $n\times n$
symmetric matrices A and B. This phenomenon was extensively studied in [Reference Bhargava5, Reference Bhargava, Gross and Wang7, Reference Bhargava, Gross and Wang8]. It is in this sense that the strategy to prove Theorem 5(b) for odd n fails spectacularly for even n – and at the very first step.
$n\times n$
symmetric matrices A and B. This phenomenon was extensively studied in [Reference Bhargava5, Reference Bhargava, Gross and Wang7, Reference Bhargava, Gross and Wang8]. It is in this sense that the strategy to prove Theorem 5(b) for odd n fails spectacularly for even n – and at the very first step.
We address this issue by replacing
![]() $f(x,y)\in {\mathcal {W}}_m^{(2)}$
by
$f(x,y)\in {\mathcal {W}}_m^{(2)}$
by
![]() $xf(x,y)$
, which is a reducible binary
$xf(x,y)$
, which is a reducible binary
![]() $(n+1)$
-ic form whose discriminant, at least generically, remains weakly divisible by
$(n+1)$
-ic form whose discriminant, at least generically, remains weakly divisible by
![]() $m^2$
. For these forms
$m^2$
. For these forms
![]() $xf(x,y)$
, we can use the lift
$xf(x,y)$
, we can use the lift
![]() $\sigma _m$
constructed in the odd case. However, since
$\sigma _m$
constructed in the odd case. However, since
![]() $xf(x,y)$
has vanishing
$xf(x,y)$
has vanishing
![]() $y^{n+1}$
term, the image of
$y^{n+1}$
term, the image of
![]() $\sigma _m$
lies within the set of pairs
$\sigma _m$
lies within the set of pairs
![]() $(A,B)$
where B is singular.
$(A,B)$
where B is singular.
The singularity of B introduces additional difficulties with respect to both the algebraic and the analytic aspects of the proof. On the algebraic side, the main new problem is that distinguished elements
![]() $(A,B)$
with B singular have at least two values for the Q-invariant, since they share at least two different common isotropic
$(A,B)$
with B singular have at least two values for the Q-invariant, since they share at least two different common isotropic
![]() $(g+1)$
-dimensional subspaces, where
$(g+1)$
-dimensional subspaces, where
![]() $n=2g+2$
. So it is no longer well defined to impose the condition that Q is large. Imposing the condition that the maximum value of Q is large does not yield sufficient savings to prove an analogue of Theorem 5(b). We thus instead construct a new invariant, termed q, such that for all but a negligible number of elements
$n=2g+2$
. So it is no longer well defined to impose the condition that Q is large. Imposing the condition that the maximum value of Q is large does not yield sufficient savings to prove an analogue of Theorem 5(b). We thus instead construct a new invariant, termed q, such that for all but a negligible number of elements
![]() $(A,B)$
in the image of our map
$(A,B)$
in the image of our map
![]() $\sigma _m$
, the invariant q is the minimum value taken by Q, and it satisfies
$\sigma _m$
, the invariant q is the minimum value taken by Q, and it satisfies
![]() $q(\sigma _m(xf(x,y)))=\pm m$
.
$q(\sigma _m(xf(x,y)))=\pm m$
.
As in the odd degree case, we once again construct fundamental domains
![]() ${\mathcal {F}}_X$
for the action of
${\mathcal {F}}_X$
for the action of
![]() $G({\mathbb {Z}})$
on
$G({\mathbb {Z}})$
on
![]() $W({\mathbb {R}})$
with height less than X, and partition such a domain into three parts: the main body, the shallow cusp and the deep cusp. However, we must now only count integer elements
$W({\mathbb {R}})$
with height less than X, and partition such a domain into three parts: the main body, the shallow cusp and the deep cusp. However, we must now only count integer elements
![]() $(A,B)$
where B is singular. The beautiful work of Eskin and Katznelson [Reference Eskin and Katznelson17] provides asymptotics for the number of singular symmetric matrices in homogenously expanding domains, but this work is not directly applicable to our case since we need to estimate the number of singular symmetric matrices B in skewed domains. To achieve this, we provide a simplification of the proof of the upper bounds in [Reference Eskin and Katznelson17], at the cost of some extra
$(A,B)$
where B is singular. The beautiful work of Eskin and Katznelson [Reference Eskin and Katznelson17] provides asymptotics for the number of singular symmetric matrices in homogenously expanding domains, but this work is not directly applicable to our case since we need to estimate the number of singular symmetric matrices B in skewed domains. To achieve this, we provide a simplification of the proof of the upper bounds in [Reference Eskin and Katznelson17], at the cost of some extra
![]() $\log $
factors, which gives us a flexible method by which to obtain upper bounds on the number of singular symmetric matrices in arbitrarily skewed domains.
$\log $
factors, which gives us a flexible method by which to obtain upper bounds on the number of singular symmetric matrices in arbitrarily skewed domains.
Accounting for the singularity of the B’s introduces complications in each region of the fundamental domain. In the main body, the fact that the singular matrices B lie on the subvariety cut out the determinant means that we cannot directly apply the large sieve, and the lack of an exact count with a power-saving error term means we also cannot directly apply a Selberg sieve to bound the number of distinguished elements. Instead, we fiber over the singular matrices B and apply the large sieve to bound the number of possible A’s. This requires us to prove new density estimates on the number of distinguished elements
![]() $(A,B)$
over
$(A,B)$
over
![]() ${\mathbb {F}}_p$
, when B is fixed.
${\mathbb {F}}_p$
, when B is fixed.
Furthermore, unlike in the odd degree case, we no longer have an automatic power-saving on the number of pairs
![]() $(A,B)\in W({\mathbb {Z}})$
lying in the shallow cusp of the fundamental domain and where B is singular. As we go closer to the deep cusp, there are regions in which imposing the condition that B is singular yields no saving whatsoever. To obtain the required bounds, we isolate this region of the shallow cusp and prove that integral elements
$(A,B)\in W({\mathbb {Z}})$
lying in the shallow cusp of the fundamental domain and where B is singular. As we go closer to the deep cusp, there are regions in which imposing the condition that B is singular yields no saving whatsoever. To obtain the required bounds, we isolate this region of the shallow cusp and prove that integral elements
![]() $(A,B)$
in them either satisfy
$(A,B)$
in them either satisfy
![]() $\Delta (A,B)=0$
or
$\Delta (A,B)=0$
or
![]() $|q(A,B)|$
is small.
$|q(A,B)|$
is small.
Finally, for the deep cusp of
![]() ${\mathcal {F}}$
, we once again use the condition that the q-invariant is large to obtain a power saving. Unlike the situation with the Q-invariant in the odd-degree case, the invariant q in the even degree case behaves more wildly and is much harder to control. This is because q is not a polynomial in the coefficients of
${\mathcal {F}}$
, we once again use the condition that the q-invariant is large to obtain a power saving. Unlike the situation with the Q-invariant in the odd-degree case, the invariant q in the even degree case behaves more wildly and is much harder to control. This is because q is not a polynomial in the coefficients of
![]() $W_0$
but rather is a minimum of the different possible values of Q. In fact, there are regions within the deep cusp where the q-invariant of elements
$W_0$
but rather is a minimum of the different possible values of Q. In fact, there are regions within the deep cusp where the q-invariant of elements
![]() $(A,B)$
are not small. However, we show that these regions correspond to an archimedean condition on the invariant binary form f of
$(A,B)$
are not small. However, we show that these regions correspond to an archimedean condition on the invariant binary form f of
![]() $(A,B)$
– namely, that the discriminant of f is much smaller than is typical for the height bound on f. Separately bounding the number of such binary forms yields the desired result.
$(A,B)$
– namely, that the discriminant of f is much smaller than is typical for the height bound on f. Separately bounding the number of such binary forms yields the desired result.
Organization of the paper
This paper is organized as follows. We begin in §3 by recalling the arithmetic invariant theory for the representations
![]() $W_n:=2\times \mathrm {{Sym}}_2(n)$
of
$W_n:=2\times \mathrm {{Sym}}_2(n)$
of
![]() $\mathrm {{SL}}_n$
and
$\mathrm {{SL}}_n$
and
![]() $2\otimes g\otimes (g+1)$
of
$2\otimes g\otimes (g+1)$
of
![]() $\mathrm {{SL}}_2\times \mathrm {{SL}}_g\times \mathrm {{SL}}_{g+1}$
. In particular, we define the fundamental invariants Q and q. We then construct our maps from
$\mathrm {{SL}}_2\times \mathrm {{SL}}_g\times \mathrm {{SL}}_{g+1}$
. In particular, we define the fundamental invariants Q and q. We then construct our maps from
![]() ${\mathcal {W}}_{m}^{(2)}$
into
${\mathcal {W}}_{m}^{(2)}$
into
![]() $W_n({\mathbb {Z}})$
when n is odd and into
$W_n({\mathbb {Z}})$
when n is odd and into
![]() $W_{n+1}({\mathbb {Z}})$
when n is even.
$W_{n+1}({\mathbb {Z}})$
when n is even.
The analytic parts of the paper are carried out in §4–6. In §4, we prove the tail estimates of Theorem 5 for odd degrees n using geometry-of-numbers techniques. In §5, we carry out the necessary groundwork to count the number of singular symmetric matrices that lie in skewed domains. Using these results, we prove the tail estimates for even degrees n in §6, completing the proof of Theorem 5. In §7, we deduce the main results, Theorems 1–4, from the tail estimates using a squarefree sieve, although the exact constants occurring in Theorems 1 and 2 remain conditional upon certain local density computations. Finally, in the Appendix, we compute the local densities of integral binary n-ic forms whose discriminants are indivisible by
![]() $p^2$
(resp., whose associated rings are maximal at p), thereby completing the proofs of Theorems 1 and 2.
$p^2$
(resp., whose associated rings are maximal at p), thereby completing the proofs of Theorems 1 and 2.
3 Invariant theory on spaces associated to binary n-ic forms
Fix a positive integer n and consider the space
![]() $V_n=\mathrm {{Sym}}^n(2)$
of binary n-ic forms of degree n. The group
$V_n=\mathrm {{Sym}}^n(2)$
of binary n-ic forms of degree n. The group
![]() $\mathrm {{SL}}_2$
acts on
$\mathrm {{SL}}_2$
acts on
![]() $V_n$
via linear change of variables: we have
$V_n$
via linear change of variables: we have
![]() $\gamma \cdot f(x,y):=f((x,y)\cdot \gamma )$
for
$\gamma \cdot f(x,y):=f((x,y)\cdot \gamma )$
for
![]() $\gamma \in \mathrm {{SL}}_2$
and
$\gamma \in \mathrm {{SL}}_2$
and
![]() $f\in V_n$
.
$f\in V_n$
.
Let
![]() $W_n=2\otimes \mathrm {{Sym}}_2(n)$
denote the space of pairs of
$W_n=2\otimes \mathrm {{Sym}}_2(n)$
denote the space of pairs of
![]() $n\times n$
symmetric matrices
$n\times n$
symmetric matrices
![]() $(A,B)$
. The group
$(A,B)$
. The group
![]() $\mathrm {{SL}}_2\times \mathrm {{SL}}_n$
acts on
$\mathrm {{SL}}_2\times \mathrm {{SL}}_n$
acts on
![]() $(A,B)$
via
$(A,B)$
via
There is a natural map
![]() $W_n\to V_n$
given by
$W_n\to V_n$
given by
sending an element of
![]() $W_n$
to its invariant binary n-ic form. The ring of
$W_n$
to its invariant binary n-ic form. The ring of
![]() $\mathrm {{SL}}_n({\mathbb {C}})$
-invariant polynomials on
$\mathrm {{SL}}_n({\mathbb {C}})$
-invariant polynomials on
![]() $W_n({\mathbb {C}})$
is freely generated by the coefficients of the invariant binary n-ic form.
$W_n({\mathbb {C}})$
is freely generated by the coefficients of the invariant binary n-ic form.
3.1 Arithmetic invariant theory for the representation
 $2\otimes \mathrm {{Sym}}_2(n)$
of
$2\otimes \mathrm {{Sym}}_2(n)$
of
 $\mathrm {{SL}}_n$
$\mathrm {{SL}}_n$
First, let
![]() $n=2g+1$
be an odd integer with
$n=2g+1$
be an odd integer with
![]() $g\geq 1$
. We recall some of the arithmetic invariant theory of the representation
$g\geq 1$
. We recall some of the arithmetic invariant theory of the representation
![]() $W:=W_n$
of
$W:=W_n$
of
![]() $\mathrm {{SL}}_n$
and its map (1) to
$\mathrm {{SL}}_n$
and its map (1) to
![]() $V:=V_n;$
see [Reference Bhargava, Gross and Wang7] for more details.
$V:=V_n;$
see [Reference Bhargava, Gross and Wang7] for more details.
Let k be a field of characteristic not
![]() $2$
. For a binary n-ic form
$2$
. For a binary n-ic form
![]() $f(x,y)=a_0x^n + \cdots + a_ny^n\in V(k)$
with
$f(x,y)=a_0x^n + \cdots + a_ny^n\in V(k)$
with
![]() $\Delta (f)\neq 0$
and
$\Delta (f)\neq 0$
and
![]() $a_0\neq 0$
, let
$a_0\neq 0$
, let
![]() $C_f$
denote the smooth hyperelliptic curve
$C_f$
denote the smooth hyperelliptic curve
![]() $z^2=f(x,y)y$
of genus g viewed as a curve in the weighted projective space
$z^2=f(x,y)y$
of genus g viewed as a curve in the weighted projective space
![]() ${\mathbb {P}}(1,1,g+1)$
. Let
${\mathbb {P}}(1,1,g+1)$
. Let
![]() $J_f$
denote the Jacobian of
$J_f$
denote the Jacobian of
![]() $C_f$
. Then the stabilizer of an element
$C_f$
. Then the stabilizer of an element
![]() $(A,B)\in W(k)$
with invariant binary form
$(A,B)\in W(k)$
with invariant binary form
![]() $f(x,y)$
is isomorphic to
$f(x,y)$
is isomorphic to
![]() $J_f[2](k)$
. The set of
$J_f[2](k)$
. The set of
![]() $\mathrm {{SL}}_n(k)$
-orbits on
$\mathrm {{SL}}_n(k)$
-orbits on
![]() $W(k)$
with invariant binary form
$W(k)$
with invariant binary form
![]() $f(x,y)$
maps injectively into
$f(x,y)$
maps injectively into
![]() $H^1(k,J_f[2])$
. An element
$H^1(k,J_f[2])$
. An element
![]() $(A,B)$
(or an
$(A,B)$
(or an
![]() $\mathrm {{SL}}_n(k)$
-orbit) is distinguished if
$\mathrm {{SL}}_n(k)$
-orbit) is distinguished if
![]() $\Delta (A,B)\neq 0$
and there exists a g-dimensional subspace defined over k that is isotropic with respect to both A and B. If
$\Delta (A,B)\neq 0$
and there exists a g-dimensional subspace defined over k that is isotropic with respect to both A and B. If
![]() $(A,B)$
is distinguished, then its
$(A,B)$
is distinguished, then its
![]() $\mathrm {{SL}}_n(k)$
-orbit corresponds to the identity element of
$\mathrm {{SL}}_n(k)$
-orbit corresponds to the identity element of
![]() $H^1(k,J_f[2])$
, and the set of these g-dimensional subspaces is in bijection with
$H^1(k,J_f[2])$
, and the set of these g-dimensional subspaces is in bijection with
![]() $J_f[2](k)$
.
$J_f[2](k)$
.
Let
![]() $W_{0}\subset W$
be the subspace of pairs of matrices whose top left
$W_{0}\subset W$
be the subspace of pairs of matrices whose top left
![]() $g\times g$
blocks are zero. Then elements
$g\times g$
blocks are zero. Then elements
![]() $(A,B)$
in
$(A,B)$
in
![]() $W_{0}(k)$
with nonzero discriminant are all distinguished since the g-dimensional subspace
$W_{0}(k)$
with nonzero discriminant are all distinguished since the g-dimensional subspace
![]() $Y_g$
spanned by the first g basis vectors is isotropic with respect to both A and B. Moreover, every distinguished element of
$Y_g$
spanned by the first g basis vectors is isotropic with respect to both A and B. Moreover, every distinguished element of
![]() $W(k)$
is
$W(k)$
is
![]() $\mathrm {{SL}}_n(k)$
-equivalent to some element in
$\mathrm {{SL}}_n(k)$
-equivalent to some element in
![]() $W_{0}(k)$
since
$W_{0}(k)$
since
![]() $\mathrm {{SL}}_n(k)$
acts transitively on the set of g-dimensional subspaces of
$\mathrm {{SL}}_n(k)$
acts transitively on the set of g-dimensional subspaces of
![]() ${\mathbb {P}}^{n-1}(k)$
. Let
${\mathbb {P}}^{n-1}(k)$
. Let
![]() $G_0$
be the maximal parabolic subgroup of
$G_0$
be the maximal parabolic subgroup of
![]() $\mathrm {{SL}}_n$
consisting of elements
$\mathrm {{SL}}_n$
consisting of elements
![]() $\gamma $
that preserve
$\gamma $
that preserve
![]() $Y_g$
. Elements of
$Y_g$
. Elements of
![]() $W_{0}$
have block matrix form
$W_{0}$
have block matrix form
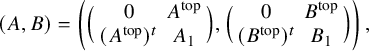 $$ \begin{align} (A,B)=\left(\Big(\begin{array}{cc}0 & A^{\mathrm{{top}}}\\ (A^{\mathrm{{top}}})^t & A_1\end{array}\Big), \Big(\begin{array}{cc}0 & B^{\mathrm{{top}}}\\ (B^{\mathrm{{top}}})^t & B_1\end{array}\Big)\right), \end{align} $$
$$ \begin{align} (A,B)=\left(\Big(\begin{array}{cc}0 & A^{\mathrm{{top}}}\\ (A^{\mathrm{{top}}})^t & A_1\end{array}\Big), \Big(\begin{array}{cc}0 & B^{\mathrm{{top}}}\\ (B^{\mathrm{{top}}})^t & B_1\end{array}\Big)\right), \end{align} $$
where
![]() $A^{\mathrm {{top}}}$
,
$A^{\mathrm {{top}}}$
,
![]() $B^{\mathrm {{top}}}$
are
$B^{\mathrm {{top}}}$
are
![]() $g\times (g+1)$
matrices and
$g\times (g+1)$
matrices and
![]() $A_1$
,
$A_1$
,
![]() $B_1$
are
$B_1$
are
![]() $(g+1)\times (g+1)$
-symmetric matrices. Meanwhile, elements of
$(g+1)\times (g+1)$
-symmetric matrices. Meanwhile, elements of
![]() $G_0$
have the block matrix form
$G_0$
have the block matrix form
An element
![]() $\gamma \in G_0$
acts on the top right
$\gamma \in G_0$
acts on the top right
![]() $g\times (g+1)$
block of elements of
$g\times (g+1)$
block of elements of
![]() $W_{0}$
by
$W_{0}$
by
where we use the superscript ‘top’ to denote the top right
![]() $g\times (g+1)$
block of an
$g\times (g+1)$
block of an
![]() $n\times n$
symmetric matrix. The action of
$n\times n$
symmetric matrix. The action of
![]() $G_0$
on
$G_0$
on
![]() $W_{0}$
restricts to an action on the space
$W_{0}$
restricts to an action on the space
![]() $U_g:=2\otimes g\otimes (g+1)$
of pairs of
$U_g:=2\otimes g\otimes (g+1)$
of pairs of
![]() $g\times (g+1)$
-matrices, Moreover, the unipotent radical
$g\times (g+1)$
-matrices, Moreover, the unipotent radical
![]() $M_{(g+1)\times g}$
of
$M_{(g+1)\times g}$
of
![]() $G_0$
acts trivially on
$G_0$
acts trivially on
![]() $U_g$
. We study the invariant theory for this action more closely in the next subsection.
$U_g$
. We study the invariant theory for this action more closely in the next subsection.
We will also need some results in the case when
![]() $n=2g+2$
is even in Section 6 (specifically in the proof of Lemma 6.7). Let
$n=2g+2$
is even in Section 6 (specifically in the proof of Lemma 6.7). Let
![]() $f(x,y) = a_0x^n + \cdots + a_ny^n\in V(k)$
with
$f(x,y) = a_0x^n + \cdots + a_ny^n\in V(k)$
with
![]() $\Delta (f)\neq 0$
and
$\Delta (f)\neq 0$
and
![]() $a_0\neq 0$
. Let
$a_0\neq 0$
. Let
![]() $L = k[x]/(f(x,1))$
. Let
$L = k[x]/(f(x,1))$
. Let
![]() $V_f(k)$
denote the set of
$V_f(k)$
denote the set of
![]() $(A,B)\in W_n(k)$
with
$(A,B)\in W_n(k)$
with
![]() $f_{A,B} = f(x,y)$
. Then
$f_{A,B} = f(x,y)$
. Then
![]() $V_f(k)$
is nonempty if and only if
$V_f(k)$
is nonempty if and only if
![]() $f_0\in k^{\times 2}N_{L/k}(L^\times )$
(see also [Reference Bhargava, Gross and Wang8, Theorem 7]). Note in particular that if
$f_0\in k^{\times 2}N_{L/k}(L^\times )$
(see also [Reference Bhargava, Gross and Wang8, Theorem 7]). Note in particular that if
![]() $f(x,y)\in V({\mathbb {R}})$
is negative definite, so that
$f(x,y)\in V({\mathbb {R}})$
is negative definite, so that
![]() $L = {\mathbb {R}}[x]/(f(x))\simeq {\mathbb {C}}^{n/2}$
and
$L = {\mathbb {R}}[x]/(f(x))\simeq {\mathbb {C}}^{n/2}$
and
![]() $a_0<0$
, then
$a_0<0$
, then
![]() $V_f({\mathbb {R}})$
is empty. However, if k is a finite field of characteristic not
$V_f({\mathbb {R}})$
is empty. However, if k is a finite field of characteristic not
![]() $2$
, then
$2$
, then
![]() $V_f(k)$
is always nonempty and the number of
$V_f(k)$
is always nonempty and the number of
![]() $\mathrm {{SL}}_n(k)$
-orbits equals the number of even degree factorizations of
$\mathrm {{SL}}_n(k)$
-orbits equals the number of even degree factorizations of
![]() $f(x,y)$
over k.
$f(x,y)$
over k.
3.2 The representation
 $2\otimes g\otimes (g+1)$
of
$2\otimes g\otimes (g+1)$
of
 $\mathrm {{SL}}_2\times \mathrm {{SL}}_g\times \mathrm {{SL}}_{g+1}$
and the Q-invariant
$\mathrm {{SL}}_2\times \mathrm {{SL}}_g\times \mathrm {{SL}}_{g+1}$
and the Q-invariant
In this section, we collect some algebraic facts about the representation
![]() $U_g;=2\otimes g\otimes (g+1)$
of the group
$U_g;=2\otimes g\otimes (g+1)$
of the group
![]() $H_g:=\mathrm {{SL}}_2\times \mathrm {{SL}}_g\times \mathrm {{SL}}_{g+1}$
. We start with the following proposition.
$H_g:=\mathrm {{SL}}_2\times \mathrm {{SL}}_g\times \mathrm {{SL}}_{g+1}$
. We start with the following proposition.
Proposition 3.1. The representation
![]() $U_g$
of
$U_g$
of
![]() ${\mathbb {G}}_m\times H_g$
is prehomogeneous (i.e., the action of
${\mathbb {G}}_m\times H_g$
is prehomogeneous (i.e., the action of
![]() ${\mathbb {G}}_m\times H_g$
on
${\mathbb {G}}_m\times H_g$
on
![]() $U_g$
has a single Zariski open orbit). Furthermore, the stabilizer in
$U_g$
has a single Zariski open orbit). Furthermore, the stabilizer in
![]() $H_g({\mathbb {C}})$
of an element in the open orbit of
$H_g({\mathbb {C}})$
of an element in the open orbit of
![]() $U_g({\mathbb {C}})$
is isomorphic to
$U_g({\mathbb {C}})$
is isomorphic to
![]() $\mathrm {{SL}}_2({\mathbb {C}})$
.
$\mathrm {{SL}}_2({\mathbb {C}})$
.
Proof. We prove this by induction on g. The assertion is clear for
![]() $g=1$
, where the representation is that of
$g=1$
, where the representation is that of
![]() ${\mathbb {G}}_m\times \mathrm {{SL}}_2\times \mathrm {{SL}}_2$
on
${\mathbb {G}}_m\times \mathrm {{SL}}_2\times \mathrm {{SL}}_2$
on
![]() $2\times 2$
matrices; the single relative invariant in this case is the determinant, and the open orbit consists of nonsingular matrices. For higher g, we note that
$2\times 2$
matrices; the single relative invariant in this case is the determinant, and the open orbit consists of nonsingular matrices. For higher g, we note that
![]() $U_g$
is a castling transform of
$U_g$
is a castling transform of
![]() $U_{g-1}$
in the sense of Sato and Kimura [Reference Sato and Kimura30, §2, Definition 10] (with
$U_{g-1}$
in the sense of Sato and Kimura [Reference Sato and Kimura30, §2, Definition 10] (with
![]() $\widetilde {G} = {\mathbb {G}}_m\times \mathrm {{SL}}_2\times \mathrm {{SL}}_g$
,
$\widetilde {G} = {\mathbb {G}}_m\times \mathrm {{SL}}_2\times \mathrm {{SL}}_g$
,
![]() $m = 2g$
and
$m = 2g$
and
![]() $n = g-1$
). As a result, the orbits of
$n = g-1$
). As a result, the orbits of
![]() ${\mathbb {G}}_m\times \mathrm {{SL}}_2\times \mathrm {{SL}}_g\times \mathrm {{SL}}_{g-1}$
on
${\mathbb {G}}_m\times \mathrm {{SL}}_2\times \mathrm {{SL}}_g\times \mathrm {{SL}}_{g-1}$
on
![]() $2\otimes g \otimes (g-1)$
are in natural one-to-one correspondence with the orbits of
$2\otimes g \otimes (g-1)$
are in natural one-to-one correspondence with the orbits of
![]() ${\mathbb {G}}_m\times \mathrm {{SL}}_2\times \mathrm {{SL}}_g\times \mathrm {{SL}}_{g+1}$
on
${\mathbb {G}}_m\times \mathrm {{SL}}_2\times \mathrm {{SL}}_g\times \mathrm {{SL}}_{g+1}$
on
![]() $2\otimes g\otimes (2g-(g-1))=2\otimes g\otimes (g+1)$
, and under this correspondence, the open orbit in
$2\otimes g\otimes (2g-(g-1))=2\otimes g\otimes (g+1)$
, and under this correspondence, the open orbit in
![]() $U_{g-1}$
maps to an open orbit in
$U_{g-1}$
maps to an open orbit in
![]() $U_g$
(cf. [Reference Sato and Kimura30, §2, Proposition 9]). Thus, all the representations
$U_g$
(cf. [Reference Sato and Kimura30, §2, Proposition 9]). Thus, all the representations
![]() $U_g$
for the action of
$U_g$
for the action of
![]() ${\mathbb {G}}_m\times H_g$
are prehomogeneous.
${\mathbb {G}}_m\times H_g$
are prehomogeneous.
Note that castling transforms preserve stabilizers over
![]() ${\mathbb {C}}$
. Since the generic stabilizer for the action of
${\mathbb {C}}$
. Since the generic stabilizer for the action of
![]() $H_1({\mathbb {C}})$
on
$H_1({\mathbb {C}})$
on
![]() $U_1({\mathbb {C}})$
is clearly isomorphic to
$U_1({\mathbb {C}})$
is clearly isomorphic to
![]() $\mathrm {{SL}}_2({\mathbb {C}})$
, it follows that this remains the generic stabilizer for the action of
$\mathrm {{SL}}_2({\mathbb {C}})$
, it follows that this remains the generic stabilizer for the action of
![]() $H_g({\mathbb {C}})$
on
$H_g({\mathbb {C}})$
on
![]() $U_g({\mathbb {C}})$
for all
$U_g({\mathbb {C}})$
for all
![]() $g\geq 1$
.
$g\geq 1$
.
Since castling transforms also preserve polynomial invariants and their irreducibility [Reference Sato and Kimura30, Proposition 18], it follows that the ring of polynomial invariants for this action of
![]() $H_g$
on
$H_g$
on
![]() $U_g$
is generated by an irreducible polynomial. We now give an explicit description of this invariant.
$U_g$
is generated by an irreducible polynomial. We now give an explicit description of this invariant.
Write an element in
![]() $U_g=2\times g\times (g+1)$
as a pair
$U_g=2\times g\times (g+1)$
as a pair
![]() $(A^{\mathrm {{top}}},B^{\mathrm {{top}}})$
of
$(A^{\mathrm {{top}}},B^{\mathrm {{top}}})$
of
![]() $g\times (g+1)$
matrices. For
$g\times (g+1)$
matrices. For
![]() $1\leq i\leq g+1$
, let
$1\leq i\leq g+1$
, let
![]() $A_i$
and
$A_i$
and
![]() $B_i$
denote the
$B_i$
denote the
![]() $g\times g$
-matrices obtained from
$g\times g$
-matrices obtained from
![]() $A^{\mathrm {{top}}}$
and
$A^{\mathrm {{top}}}$
and
![]() $B^{\mathrm {{top}}}$
, respectively, by deleting the ith column. Define the binary g-ic form
$B^{\mathrm {{top}}}$
, respectively, by deleting the ith column. Define the binary g-ic form
![]() $f_i(x,y)$
to be
$f_i(x,y)$
to be
![]() $(-1)^{i+1}\det (A_ix-B_iy)$
. Consider the
$(-1)^{i+1}\det (A_ix-B_iy)$
. Consider the
![]() $(g+1)\times (g+1)$
matrix C whose
$(g+1)\times (g+1)$
matrix C whose
![]() $(i,j)$
-entry is the jth-coefficient of
$(i,j)$
-entry is the jth-coefficient of
![]() $f_i(x,y)$
. Taking the determinant of C yields a polynomial
$f_i(x,y)$
. Taking the determinant of C yields a polynomial
![]() $Q=Q(A^{\mathrm {{top}}},B^{\mathrm {{top}}})$
in the coordinates of
$Q=Q(A^{\mathrm {{top}}},B^{\mathrm {{top}}})$
in the coordinates of
![]() $U_g$
. The polynomial Q is the hyperdeterminant of the
$U_g$
. The polynomial Q is the hyperdeterminant of the
![]() $2\times g \times (g+1)$
matrix
$2\times g \times (g+1)$
matrix
![]() $(A^{\mathrm {{top}}},B^{\mathrm {{top}}})$
(cf. [Reference Gelfond, Kapranov and Zelevinsky18, Chapter 14, Theorem 3.18] with
$(A^{\mathrm {{top}}},B^{\mathrm {{top}}})$
(cf. [Reference Gelfond, Kapranov and Zelevinsky18, Chapter 14, Theorem 3.18] with
![]() $m = g$
,
$m = g$
,
![]() $n = g+1$
,
$n = g+1$
,
![]() $p = 2$
). As a consequence, it is irreducible and invariant under the action of
$p = 2$
). As a consequence, it is irreducible and invariant under the action of
![]() $H_g$
on
$H_g$
on
![]() $U_g$
and thus generates the ring of polynomials for the action of
$U_g$
and thus generates the ring of polynomials for the action of
![]() $H_g$
on
$H_g$
on
![]() $U_g$
.
$U_g$
.
Let
![]() $n=2g+1$
again be an odd integer. We return to the representation
$n=2g+1$
again be an odd integer. We return to the representation
![]() $W_{0}$
of
$W_{0}$
of
![]() $G_0$
. Given an element
$G_0$
. Given an element
![]() $(A,B)\in W_{0}$
, recall that we obtain an element
$(A,B)\in W_{0}$
, recall that we obtain an element
![]() $(A^{\mathrm {{top}}},B^{\mathrm {{top}}})\in U_g$
by taking the top right
$(A^{\mathrm {{top}}},B^{\mathrm {{top}}})\in U_g$
by taking the top right
![]() $g\times (g+1)$
blocks of A and B. We define the Q-invariant of
$g\times (g+1)$
blocks of A and B. We define the Q-invariant of
![]() $(A,B)\in W_{0}$
as the Q-invariant of
$(A,B)\in W_{0}$
as the Q-invariant of
![]() $(A^{\mathrm {{top}}},B^{\mathrm {{top}}})$
:
$(A^{\mathrm {{top}}},B^{\mathrm {{top}}})$
:
Then the Q-invariant is a relative invariant for
![]() $G_0$
. More precisely, for any
$G_0$
. More precisely, for any
![]() $\gamma \in G_0$
in the block matrix form (3), we have
$\gamma \in G_0$
in the block matrix form (3), we have
since
![]() $\det (\gamma _1)\det (\gamma _2)=1$
. If
$\det (\gamma _1)\det (\gamma _2)=1$
. If
![]() $\gamma \in G_0({\mathbb {Z}})$
, then we have
$\gamma \in G_0({\mathbb {Z}})$
, then we have
![]() $\det (\gamma _1)=\det (\gamma _2)=\pm 1$
. Hence, the absolute value
$\det (\gamma _1)=\det (\gamma _2)=\pm 1$
. Hence, the absolute value
![]() $|Q|$
of Q is an invariant for the action of
$|Q|$
of Q is an invariant for the action of
![]() $G_0({\mathbb {Z}})$
on
$G_0({\mathbb {Z}})$
on
![]() $W_{0}({\mathbb {Z}})$
.
$W_{0}({\mathbb {Z}})$
.
3.3 Divisibility properties of
 $\Delta $
when restricted to
$\Delta $
when restricted to
 $W_{0}$
$W_{0}$
Let
![]() $n=2g+1$
be an odd integer. Write the coordinates on
$n=2g+1$
be an odd integer. Write the coordinates on
![]() $W_{0}$
as
$W_{0}$
as
![]() $a_{ij},b_{ij}$
with
$a_{ij},b_{ij}$
with
![]() $i,j$
in the appropriate ranges. Let R denote the ring of regular functions of
$i,j$
in the appropriate ranges. Let R denote the ring of regular functions of
![]() $W_0$
over
$W_0$
over
![]() ${\mathbb {Z}}$
(i.e.,
${\mathbb {Z}}$
(i.e.,
![]() $R={\mathbb {Z}}[W_0]={\mathbb {Z}}[a_{ij},b_{ij}]$
). Consider the discriminant polynomial
$R={\mathbb {Z}}[W_0]={\mathbb {Z}}[a_{ij},b_{ij}]$
). Consider the discriminant polynomial
![]() $\Delta \in R$
given by
$\Delta \in R$
given by
![]() $\Delta (A,B):=\Delta (f_{A,B})$
. In this section, we prove that
$\Delta (A,B):=\Delta (f_{A,B})$
. In this section, we prove that
![]() $Q^2\mid \Delta $
as polynomials in R, along with another useful divisibility result.
$Q^2\mid \Delta $
as polynomials in R, along with another useful divisibility result.
Let Z be the closed subvariety of
![]() $W_{0}$
consisting of elements
$W_{0}$
consisting of elements
![]() $(A,B)$
with
$(A,B)$
with
![]() $\Delta (A,B)=0$
, and let
$\Delta (A,B)=0$
, and let
![]() $Y\subset Z$
denote the closed subvariety of
$Y\subset Z$
denote the closed subvariety of
![]() $W_{0}$
consisting of elements
$W_{0}$
consisting of elements
![]() $(A,B)$
such that
$(A,B)$
such that
![]() $f_{A,B}$
is either divisible by the cube of a binary form with degree
$f_{A,B}$
is either divisible by the cube of a binary form with degree
![]() $\geq 1$
or the square of a binary form with degree
$\geq 1$
or the square of a binary form with degree
![]() $\geq 2$
. Both of these varieties Y and Z are defined over
$\geq 2$
. Both of these varieties Y and Z are defined over
![]() ${\mathbb {Z}}$
and are clearly
${\mathbb {Z}}$
and are clearly
![]() $\mathrm {{SL}}_2\times G_0$
-invariant.
$\mathrm {{SL}}_2\times G_0$
-invariant.
Our first result states that the variety in
![]() $W_{0}$
cut out by
$W_{0}$
cut out by
![]() $Q=0$
does not lie in Y.
$Q=0$
does not lie in Y.
Proposition 3.2. Let
![]() $(A,B) = ((a_{ij})_{ij},(b_{ij})_{ij}) \in W_0(R)$
be the generic element. Then
$(A,B) = ((a_{ij})_{ij},(b_{ij})_{ij}) \in W_0(R)$
be the generic element. Then
Proof. Fix an odd prime p. Let
![]() $f(x,y)$
be an element of
$f(x,y)$
be an element of
![]() $V({\mathbb {Z}})$
, such that the reduction of
$V({\mathbb {Z}})$
, such that the reduction of
![]() $f(x,y)$
modulo p factors as
$f(x,y)$
modulo p factors as
![]() $x^2h(x,y)$
, where h is irreducible. In particular,
$x^2h(x,y)$
, where h is irreducible. In particular,
![]() $f(x,y)$
mod p is not divisible by either the cube of a binary form with degree
$f(x,y)$
mod p is not divisible by either the cube of a binary form with degree
![]() $\geq 1$
, or the square of a binary form with degree
$\geq 1$
, or the square of a binary form with degree
![]() $\geq 2$
. Let
$\geq 2$
. Let
![]() $(A_f,B_f)\in W_{0}({\mathbb {Z}})$
be an element with invariant binary n-ic form equal to f and
$(A_f,B_f)\in W_{0}({\mathbb {Z}})$
be an element with invariant binary n-ic form equal to f and
![]() $Q(A_f,B_f) = p$
. Such an element
$Q(A_f,B_f) = p$
. Such an element
![]() $(A_f,B_f)$
is constructed in the next subsection (see (9) with
$(A_f,B_f)$
is constructed in the next subsection (see (9) with
![]() $m = p$
).
$m = p$
).
Let
![]() $\pi :R\rightarrow {\mathbb {Z}}$
denote the specialization map assigning integer values to
$\pi :R\rightarrow {\mathbb {Z}}$
denote the specialization map assigning integer values to
![]() $a_{ij},b_{ij}$
such that
$a_{ij},b_{ij}$
such that
Then
![]() $\pi (Q) = p$
and so
$\pi (Q) = p$
and so
![]() $\pi $
induces a map
$\pi $
induces a map
![]() $R/(Q) \rightarrow {\mathbb {F}}_p$
. Since
$R/(Q) \rightarrow {\mathbb {F}}_p$
. Since
![]() $(A_f,B_f)\text { mod }p\notin Y({\mathbb {F}}_p)$
, we see that
$(A_f,B_f)\text { mod }p\notin Y({\mathbb {F}}_p)$
, we see that
![]() $(A,B)\text { mod }Q\notin Y(R/(Q))$
.
$(A,B)\text { mod }Q\notin Y(R/(Q))$
.
The next lemma, which follows from a direct computation, gives the Q-invariant for elements in
![]() $W_{0}$
having a specific form.
$W_{0}$
having a specific form.
Lemma 3.3. Let k be a field and let
![]() $(A,B)\in W_{0}(k)$
be an element such that the top right
$(A,B)\in W_{0}(k)$
be an element such that the top right
![]() $g\times (g+1)$
blocks of
$g\times (g+1)$
blocks of
![]() $(A,B)$
are of the following form:
$(A,B)$
are of the following form:

Then
Next, we have the following proposition that gives a normal form for elements
![]() $(A,B)\not \in Y$
whose Q-invariant is
$(A,B)\not \in Y$
whose Q-invariant is
![]() $0$
.
$0$
.
Proposition 3.4. Let k be a field. Let
![]() $(A,B)$
be an element of
$(A,B)$
be an element of
![]() $W_{0}(k)\backslash Y(k)$
such that
$W_{0}(k)\backslash Y(k)$
such that
![]() $Q(A,B)=0$
. Then
$Q(A,B)=0$
. Then
![]() $(A,B)$
is
$(A,B)$
is
![]() $\mathrm {{SL}}_2(k)\times G_0(k)$
-equivalent to an element of the form
$\mathrm {{SL}}_2(k)\times G_0(k)$
-equivalent to an element of the form
![]() $(A',B')$
where the top right
$(A',B')$
where the top right
![]() $g\times (g+1)$
blocks of
$g\times (g+1)$
blocks of
![]() $A'$
and
$A'$
and
![]() $B'$
are given by
$B'$
are given by
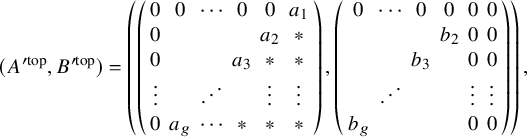
where
![]() $a_1,\ldots ,a_g,b_2,\ldots ,b_g\in k^\times .$
In the displayed matrices above, any empty entry is
$a_1,\ldots ,a_g,b_2,\ldots ,b_g\in k^\times .$
In the displayed matrices above, any empty entry is
![]() $0$
.
$0$
.
Proof. The action of
![]() $G_0(k)$
allows us to perform simultaneous row operations and simultaneous column operations on
$G_0(k)$
allows us to perform simultaneous row operations and simultaneous column operations on
![]() $(A^{\mathrm {{top}}},B^{\mathrm {{top}}})$
. As a first step, we perform column operations to ensure that the rightmost column of
$(A^{\mathrm {{top}}},B^{\mathrm {{top}}})$
. As a first step, we perform column operations to ensure that the rightmost column of
![]() $B^{\mathrm {{top}}}$
is
$B^{\mathrm {{top}}}$
is
![]() $0$
. Next, recall that the Q-invariant of
$0$
. Next, recall that the Q-invariant of
![]() $(A,B)$
is the determinant of the
$(A,B)$
is the determinant of the
![]() $(g+1)\times (g+1)$
matrix C, whose rows come from the coefficients of the
$(g+1)\times (g+1)$
matrix C, whose rows come from the coefficients of the
![]() $g\times g$
minors of
$g\times g$
minors of
![]() $A^{\mathrm {{top}}} x-B^{\mathrm {{top}}} y$
. It follows that row operations on
$A^{\mathrm {{top}}} x-B^{\mathrm {{top}}} y$
. It follows that row operations on
![]() $(A^{\mathrm {{top}}},B^{\mathrm {{top}}})$
leave C unchanged, while adding
$(A^{\mathrm {{top}}},B^{\mathrm {{top}}})$
leave C unchanged, while adding
![]() $\alpha $
times the i-th columns of
$\alpha $
times the i-th columns of
![]() $A^{\mathrm {{top}}},B^{\mathrm {{top}}}$
to the j-th column has the effect of adding
$A^{\mathrm {{top}}},B^{\mathrm {{top}}}$
to the j-th column has the effect of adding
![]() $\alpha $
times the j-th row of C to the i-th row of C and leaving the rest unchanged. Since
$\alpha $
times the j-th row of C to the i-th row of C and leaving the rest unchanged. Since
![]() $\det (C)=Q(A^{\mathrm {{top}}},B^{\mathrm {{top}}})=0$
, it follows that by adding multiples of the last columns of
$\det (C)=Q(A^{\mathrm {{top}}},B^{\mathrm {{top}}})=0$
, it follows that by adding multiples of the last columns of
![]() $A^{\mathrm {{top}}},B^{\mathrm {{top}}}$
to the other columns, we may assume that the last row of C is
$A^{\mathrm {{top}}},B^{\mathrm {{top}}}$
to the other columns, we may assume that the last row of C is
![]() $0$
. Denoting the
$0$
. Denoting the
![]() $g\times g$
matrices obtained by removing the last columns of
$g\times g$
matrices obtained by removing the last columns of
![]() $A^{\mathrm {{top}}}$
and
$A^{\mathrm {{top}}}$
and
![]() $B^{\mathrm {{top}}}$
by M and N, respectively, we have
$B^{\mathrm {{top}}}$
by M and N, respectively, we have
![]() $\det (Mx - Ny) = 0$
.
$\det (Mx - Ny) = 0$
.
We next claim that by performing simultaneous row and column operations on
![]() $(M,N)$
, we may bring M and N in the form of the first g columns of
$(M,N)$
, we may bring M and N in the form of the first g columns of
![]() $A^{\prime \,\mathrm {{top}}}$
and
$A^{\prime \,\mathrm {{top}}}$
and
![]() $B^{\prime \,\mathrm {{top}}}$
, respectively, for
$B^{\prime \,\mathrm {{top}}}$
, respectively, for
![]() $(A^{\prime \,\mathrm {{top}}},B^{\prime \,\mathrm {{top}}})$
as given in (7) with
$(A^{\prime \,\mathrm {{top}}},B^{\prime \,\mathrm {{top}}})$
as given in (7) with
![]() $b_i\neq 0$
for all
$b_i\neq 0$
for all
![]() $2\leq i\leq g$
. Since
$2\leq i\leq g$
. Since
![]() $\det (M)=0$
, after appropriate column operations, we may assume that the first column of M is
$\det (M)=0$
, after appropriate column operations, we may assume that the first column of M is
![]() $0$
. Now the first column of N cannot be identically
$0$
. Now the first column of N cannot be identically
![]() $0$
for otherwise, the invariant binary form of
$0$
for otherwise, the invariant binary form of
![]() $(A,B)$
has a factor of the form
$(A,B)$
has a factor of the form
![]() $h(x,y)^2$
with
$h(x,y)^2$
with
![]() $\deg h = g$
, contradicting
$\deg h = g$
, contradicting
![]() $(A,B)\notin Y(k)$
. By applying row operations, we may ensure that the bottom left entry of N is
$(A,B)\notin Y(k)$
. By applying row operations, we may ensure that the bottom left entry of N is
![]() $b_g\neq 0$
and the rest of the first column of N is
$b_g\neq 0$
and the rest of the first column of N is
![]() $0$
. We then use this nonzero cofficient
$0$
. We then use this nonzero cofficient
![]() $b_g$
to clear out the rest of the bottom row of N (without changing M).
$b_g$
to clear out the rest of the bottom row of N (without changing M).
Let
![]() $M_1$
and
$M_1$
and
![]() $N_1$
denote the top right
$N_1$
denote the top right
![]() $(g-1)\times (g-1)$
block of M and N. Then
$(g-1)\times (g-1)$
block of M and N. Then
![]() $\det (Mx - Ny) = (-1)^{g}b_g y\det (M_1x - N_1y).$
Hence,
$\det (Mx - Ny) = (-1)^{g}b_g y\det (M_1x - N_1y).$
Hence,
![]() $\det (M_1x - N_1y) = 0$
and the first column of
$\det (M_1x - N_1y) = 0$
and the first column of
![]() $M_1$
can be made
$M_1$
can be made
![]() $0$
. As in the previous case, all the coefficients of the first column of
$0$
. As in the previous case, all the coefficients of the first column of
![]() $N_1$
can be made
$N_1$
can be made
![]() $0$
except for the bottom left entry, which is
$0$
except for the bottom left entry, which is
![]() $b_{g-1}\neq 0$
. We then clear out the bottom row of
$b_{g-1}\neq 0$
. We then clear out the bottom row of
![]() $N_1$
as before. Proceeding in this way, we transform the first
$N_1$
as before. Proceeding in this way, we transform the first
![]() $g-1$
columns of M and N to be in the required form. Since the
$g-1$
columns of M and N to be in the required form. Since the
![]() $b_i$
’s are nonzero for
$b_i$
’s are nonzero for
![]() $2\leq i\leq g$
, and since
$2\leq i\leq g$
, and since
![]() $\det (Mx-Ny)=0$
, it follows that the top right coefficients of M and N are
$\det (Mx-Ny)=0$
, it follows that the top right coefficients of M and N are
![]() $0$
, completing the proof of the claim.
$0$
, completing the proof of the claim.
Note that this transformation of M and N did not change the last column of
![]() $B^{\mathrm {{top}}}$
, which remains
$B^{\mathrm {{top}}}$
, which remains
![]() $0$
. Thus, to complete the proof of Proposition 3.4, it remains to show that
$0$
. Thus, to complete the proof of Proposition 3.4, it remains to show that
![]() $a_i\neq 0$
for
$a_i\neq 0$
for
![]() $1\leq i\leq g$
. Since the first row and column of
$1\leq i\leq g$
. Since the first row and column of
![]() $B'$
are
$B'$
are
![]() $0$
, we see that
$0$
, we see that
![]() $x^2a_1^2\mid f_{A',B'}$
. Hence,
$x^2a_1^2\mid f_{A',B'}$
. Hence,
![]() $a_1\neq 0$
. Suppose for contradiction that
$a_1\neq 0$
. Suppose for contradiction that
![]() $i=2,\ldots ,g$
is the smallest index such that
$i=2,\ldots ,g$
is the smallest index such that
![]() $a_i = 0$
. Then we may clear out the i-th row of
$a_i = 0$
. Then we may clear out the i-th row of
![]() $A'$
using the second up to the
$A'$
using the second up to the
![]() $(i-1)$
-th rows of
$(i-1)$
-th rows of
![]() $A'$
. That is,
$A'$
. That is,
![]() $(A',B')$
is
$(A',B')$
is
![]() $\mathrm {{SL}}_n(k)$
-equivalent to some
$\mathrm {{SL}}_n(k)$
-equivalent to some
![]() $(A",B")$
where the only nonzero entries in the i-th row and the i-th column of
$(A",B")$
where the only nonzero entries in the i-th row and the i-th column of
![]() $A"$
appear in the last entry. This allows us to factor out an extra factor of
$A"$
appear in the last entry. This allows us to factor out an extra factor of
![]() $y^2$
in
$y^2$
in
![]() $\det (A"x - B"y)=\pm f_{A,B}$
, contradicting the assumption that
$\det (A"x - B"y)=\pm f_{A,B}$
, contradicting the assumption that
![]() $(A,B)\notin Y(k)$
since we already had
$(A,B)\notin Y(k)$
since we already had
![]() $x^2\mid f_{A,B}$
.
$x^2\mid f_{A,B}$
.
We are now ready to prove that
![]() $Q^2\mid \Delta $
:
$Q^2\mid \Delta $
:
Theorem 3.5. We have
![]() $Q^2\mid \Delta $
in
$Q^2\mid \Delta $
in
![]() ${\mathbb {Z}}[W_{0}]$
.
${\mathbb {Z}}[W_{0}]$
.
Proof. Let
![]() $(A,B)\in W_{0}(R)$
be the generic element. We begin by proving that
$(A,B)\in W_{0}(R)$
be the generic element. We begin by proving that
![]() $(A,B)\in Z(R/(Q))$
, or equivalently that
$(A,B)\in Z(R/(Q))$
, or equivalently that
![]() $Q\mid \Delta $
in R. Let
$Q\mid \Delta $
in R. Let
![]() $(\bar {A},\bar {B})\in W_{0}(R/(Q))$
denote the reduction of
$(\bar {A},\bar {B})\in W_{0}(R/(Q))$
denote the reduction of
![]() $(A,B)$
mod Q, and let F denote the field of fractions of
$(A,B)$
mod Q, and let F denote the field of fractions of
![]() $R/(Q)$
. By Proposition 3.2, we know
$R/(Q)$
. By Proposition 3.2, we know
![]() $(\bar {A},\bar {B})\notin Y(F)$
. Since
$(\bar {A},\bar {B})\notin Y(F)$
. Since
![]() $Q(\bar {A},\bar {B}) = 0$
, by Proposition 3.4, there exists
$Q(\bar {A},\bar {B}) = 0$
, by Proposition 3.4, there exists
![]() $\gamma \in \mathrm {{SL}}_2(F)\times G_0(F)$
such that
$\gamma \in \mathrm {{SL}}_2(F)\times G_0(F)$
such that
![]() $\gamma (\bar {A},\bar {B})=(A',B')$
, where
$\gamma (\bar {A},\bar {B})=(A',B')$
, where
![]() $(A^{\prime \,\mathrm {{top}}},B^{\prime \,\mathrm {{top}}})$
is of the form (7). The invariant binary form of
$(A^{\prime \,\mathrm {{top}}},B^{\prime \,\mathrm {{top}}})$
is of the form (7). The invariant binary form of
![]() $(A',B')$
has a factor of
$(A',B')$
has a factor of
![]() $x^2$
, and so
$x^2$
, and so
![]() $(A',B')\in Z(F)$
. Since Z is
$(A',B')\in Z(F)$
. Since Z is
![]() $\mathrm {{SL}}_2\times G_0$
-invariant, we see that
$\mathrm {{SL}}_2\times G_0$
-invariant, we see that
![]() $(\bar {A},\bar {B})\in Z(F)$
.
$(\bar {A},\bar {B})\in Z(F)$
.
Since
![]() $Q\mid \Delta $
in R, there exists an element
$Q\mid \Delta $
in R, there exists an element
![]() $\delta \in R$
such that
$\delta \in R$
such that
![]() $\Delta =Q\delta $
. Let
$\Delta =Q\delta $
. Let
![]() $Z_1$
denote the closed subvariety of
$Z_1$
denote the closed subvariety of
![]() $W_{0}$
cut out by
$W_{0}$
cut out by
![]() $\delta $
. It now suffices to prove that
$\delta $
. It now suffices to prove that
![]() $Q\mid \delta $
or, equivalently, that the generic element
$Q\mid \delta $
or, equivalently, that the generic element
![]() $(A,B)$
belongs to
$(A,B)$
belongs to
![]() $Z_1(R/Q)$
. We claim that for any field k, and every element
$Z_1(R/Q)$
. We claim that for any field k, and every element
![]() $(A,B)\in W_{0}(k)$
such that
$(A,B)\in W_{0}(k)$
such that
![]() $(A^{\mathrm {{top}}},B^{\mathrm {{top}}})$
has the form (7), we have
$(A^{\mathrm {{top}}},B^{\mathrm {{top}}})$
has the form (7), we have
![]() $\delta (A,B)=0$
. Indeed, let
$\delta (A,B)=0$
. Indeed, let
![]() $(A,B)$
be such an element. Let
$(A,B)$
be such an element. Let
![]() $(A^{(\epsilon )},B^{(\epsilon )})\in W_{0}(k[\epsilon ])$
be such that
$(A^{(\epsilon )},B^{(\epsilon )})\in W_{0}(k[\epsilon ])$
be such that
![]() $A^{(\epsilon )}=A$
, the
$A^{(\epsilon )}=A$
, the
![]() $(1,n-1)$
-entry and the
$(1,n-1)$
-entry and the
![]() $(n-1,1)$
-entry of
$(n-1,1)$
-entry of
![]() $B^{(\epsilon )}$
equal
$B^{(\epsilon )}$
equal
![]() $\epsilon $
, and the other coefficients of
$\epsilon $
, and the other coefficients of
![]() $B^{(\epsilon )}$
are the same as those of B. By Lemma 3.3, we have
$B^{(\epsilon )}$
are the same as those of B. By Lemma 3.3, we have
Moreover,
![]() $\epsilon ^2$
divides the
$\epsilon ^2$
divides the
![]() $y^n$
-coefficient of
$y^n$
-coefficient of
![]() $f_{A^{(\epsilon )},B^{(\epsilon )}}$
and
$f_{A^{(\epsilon )},B^{(\epsilon )}}$
and
![]() $\epsilon $
divides the
$\epsilon $
divides the
![]() $xy^{n-1}$
-coefficient of
$xy^{n-1}$
-coefficient of
![]() $f_{A^{(\epsilon )},B^{(\epsilon )}}$
. Hence,
$f_{A^{(\epsilon )},B^{(\epsilon )}}$
. Hence,
![]() $\epsilon ^2\mid \Delta (A^{(\epsilon )},B^{(\epsilon )})$
, which implies (since
$\epsilon ^2\mid \Delta (A^{(\epsilon )},B^{(\epsilon )})$
, which implies (since
![]() $\epsilon ^2\nmid Q(A^{(\epsilon )},B^{(\epsilon )})$
) that
$\epsilon ^2\nmid Q(A^{(\epsilon )},B^{(\epsilon )})$
) that
![]() $\epsilon \mid \delta (A^{(\epsilon )},B^{(\epsilon )})$
. Since
$\epsilon \mid \delta (A^{(\epsilon )},B^{(\epsilon )})$
. Since
![]() $(A,B)$
is obtained from
$(A,B)$
is obtained from
![]() $(A^{(\epsilon )},B^{(\epsilon )})$
by setting
$(A^{(\epsilon )},B^{(\epsilon )})$
by setting
![]() $\epsilon =0$
, we have
$\epsilon =0$
, we have
![]() $\delta (A,B)=0$
. We have proven that the generic element
$\delta (A,B)=0$
. We have proven that the generic element
![]() $(A,B)\in W_{0}(R)$
belongs to
$(A,B)\in W_{0}(R)$
belongs to
![]() $Z_1(R/(Q))$
. Therefore,
$Z_1(R/(Q))$
. Therefore,
![]() $Q\mid \delta $
.
$Q\mid \delta $
.
We end this section with another divisibility result for
![]() $\Delta $
, which will be used in §6.
$\Delta $
, which will be used in §6.
Proposition 3.6. We have
![]() $\det (A^{\mathrm {{top}}} (A^{\mathrm {{top}}})^t)\det (B^{\mathrm {{top}}} (B^{\mathrm {{top}}})^t) \mid \Delta $
as elements in
$\det (A^{\mathrm {{top}}} (A^{\mathrm {{top}}})^t)\det (B^{\mathrm {{top}}} (B^{\mathrm {{top}}})^t) \mid \Delta $
as elements in
![]() ${\mathbb {Z}}[W_{0}]$
.
${\mathbb {Z}}[W_{0}]$
.
Proof. It suffices to prove that
![]() $\det (B^{\mathrm {{top}}} (B^{\mathrm {{top}}})^t)$
divides
$\det (B^{\mathrm {{top}}} (B^{\mathrm {{top}}})^t)$
divides
![]() $\Delta $
in
$\Delta $
in
![]() ${\mathbb {Z}}[W_{0}]$
. Suppose
${\mathbb {Z}}[W_{0}]$
. Suppose
![]() $(A,B)\in W_{0}({\mathbb {C}})$
with
$(A,B)\in W_{0}({\mathbb {C}})$
with
![]() $\det (B^{\mathrm {{top}}} (B^{\mathrm {{top}}})^t) = 0$
. Then
$\det (B^{\mathrm {{top}}} (B^{\mathrm {{top}}})^t) = 0$
. Then
![]() $B^{\mathrm {{top}}}$
does not have full rank. Hence, there exists some nonzero
$B^{\mathrm {{top}}}$
does not have full rank. Hence, there exists some nonzero
![]() $v\in \text {Span}_{\mathbb {C}}\{e_1,\ldots ,e_g\}$
such that
$v\in \text {Span}_{\mathbb {C}}\{e_1,\ldots ,e_g\}$
such that
![]() $Bv = 0$
. However, any such v is isotropic with respect to A. As a result,
$Bv = 0$
. However, any such v is isotropic with respect to A. As a result,
![]() $\Delta (A,B) = 0$
. Thus, by the Nullstellensatz,
$\Delta (A,B) = 0$
. Thus, by the Nullstellensatz,
![]() $\det (B^{\mathrm {{top}}} (B^{\mathrm {{top}}})^t) \mid c \Delta ^{d}$
in
$\det (B^{\mathrm {{top}}} (B^{\mathrm {{top}}})^t) \mid c \Delta ^{d}$
in
![]() ${\mathbb {Z}}[W_{0}]$
for some nonzero integer c and positive integer d.
${\mathbb {Z}}[W_{0}]$
for some nonzero integer c and positive integer d.
Define
![]() $P_g\in {\mathbb {Z}}[M_{g\times (g+1)}]$
by
$P_g\in {\mathbb {Z}}[M_{g\times (g+1)}]$
by
![]() $P_g(M) = \det (MM^t)$
. For the purpose of proving Proposition 3.6, it suffices to prove that
$P_g(M) = \det (MM^t)$
. For the purpose of proving Proposition 3.6, it suffices to prove that
![]() $P_g$
is squarefree in
$P_g$
is squarefree in
![]() ${\mathbb {Z}}[M_{g\times (g+1)}]$
. We proceed by induction on g. Denote the
${\mathbb {Z}}[M_{g\times (g+1)}]$
. We proceed by induction on g. Denote the
![]() $(i,j)$
-entry of any
$(i,j)$
-entry of any
![]() $M\in M_{g\times (g+1)}$
by
$M\in M_{g\times (g+1)}$
by
![]() $u_{ij}$
. When
$u_{ij}$
. When
![]() $g = 1$
, we have
$g = 1$
, we have
![]() $P_1 = u_{11}^2 + u_{12}^2$
, which is squarefree in
$P_1 = u_{11}^2 + u_{12}^2$
, which is squarefree in
![]() ${\mathbb {Z}}[u_{11},u_{12}]$
. For general
${\mathbb {Z}}[u_{11},u_{12}]$
. For general
![]() $g\geq 2$
, consider
$g\geq 2$
, consider
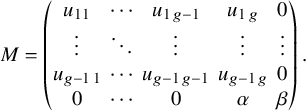 $$ \begin{align*}M = \begin{pmatrix} u_{11} & \cdots & u_{1\,g-1} & u_{1\,g} & 0\\ \vdots & \ddots & \vdots & \vdots & \vdots \\ u_{g-1\, 1} & \cdots & u_{g-1\,g-1} & u_{g-1\,g} & 0\\ 0&\cdots&0&\alpha&\beta \end{pmatrix}.\end{align*} $$
$$ \begin{align*}M = \begin{pmatrix} u_{11} & \cdots & u_{1\,g-1} & u_{1\,g} & 0\\ \vdots & \ddots & \vdots & \vdots & \vdots \\ u_{g-1\, 1} & \cdots & u_{g-1\,g-1} & u_{g-1\,g} & 0\\ 0&\cdots&0&\alpha&\beta \end{pmatrix}.\end{align*} $$
Then
where
![]() $D_{g-1}$
is the determinant of the top left
$D_{g-1}$
is the determinant of the top left
![]() $(g-1)\times (g-1)$
block of M. Any square factor of
$(g-1)\times (g-1)$
block of M. Any square factor of
![]() $\det (MM^t)$
must be a common square factor of
$\det (MM^t)$
must be a common square factor of
![]() $P_{g-1}$
and
$P_{g-1}$
and
![]() $D_{g-1}^2$
, which can only be
$D_{g-1}^2$
, which can only be
![]() $\pm 1$
since
$\pm 1$
since
![]() $P_{g-1}$
is squarefree by induction. We have shown that
$P_{g-1}$
is squarefree by induction. We have shown that
![]() $P_g$
is squarefree even after setting certain variables to
$P_g$
is squarefree even after setting certain variables to
![]() $0$
. Therefore,
$0$
. Therefore,
![]() $P_g$
is squarefree in
$P_g$
is squarefree in
![]() ${\mathbb {Z}}[M_{g\times (g+1)}]$
.
${\mathbb {Z}}[M_{g\times (g+1)}]$
.
3.4 Embedding
 ${\mathcal {W}}_{m,n}^{\mathrm {{{(2)}}}}$
into
${\mathcal {W}}_{m,n}^{\mathrm {{{(2)}}}}$
into
 $W_n({\mathbb {Z}})$
, for n odd
$W_n({\mathbb {Z}})$
, for n odd
Let
![]() $n=2g+1$
be an odd integer, and set
$n=2g+1$
be an odd integer, and set
![]() $W=W_n$
. For an odd squarefree integer
$W=W_n$
. For an odd squarefree integer
![]() $m>0$
, let
$m>0$
, let
![]() ${\mathcal {W}}_m^{\mathrm {{{(2)}}}}={\mathcal {W}}_{m,n}^{\mathrm {{{(2)}}}}$
denote the set of integer n-ic binary forms whose discriminants are weakly divisible by
${\mathcal {W}}_m^{\mathrm {{{(2)}}}}={\mathcal {W}}_{m,n}^{\mathrm {{{(2)}}}}$
denote the set of integer n-ic binary forms whose discriminants are weakly divisible by
![]() $p^2$
for every prime factor p of m. Fix an element
$p^2$
for every prime factor p of m. Fix an element
![]() $f(x,y)\in {\mathcal {W}}_m^{\mathrm {{{(2)}}}}$
. Then just as shown in [Reference Bhargava, Shankar and Wang11, §3.2], there exists an
$f(x,y)\in {\mathcal {W}}_m^{\mathrm {{{(2)}}}}$
. Then just as shown in [Reference Bhargava, Shankar and Wang11, §3.2], there exists an
![]() $\mathrm {{SL}}_2({\mathbb {Z}})$
-change of variable such that
$\mathrm {{SL}}_2({\mathbb {Z}})$
-change of variable such that
![]() $f((x,y)\gamma )$
has the form
$f((x,y)\gamma )$
has the form
for some integers
![]() $b_0,\ldots ,b_n$
and where m and
$b_0,\ldots ,b_n$
and where m and
![]() $b_0$
are coprime.
$b_0$
are coprime.
Consider the following pair of matrices:
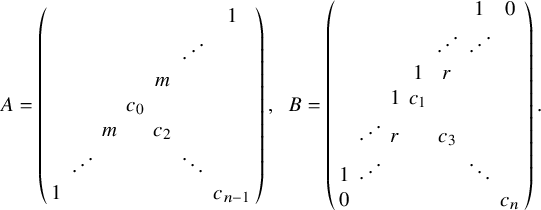 $$ \begin{align} A = \left(\begin{array}{ccccccc}&&&&&&1\\&&&&&\unicode{x22F0}&\\ &&&&m&&\\ &&&c_0&&& \\ &&m&&c_{2}&&\\ &\unicode{x22F0}&&&&\ddots&\\ 1&&&&&&c_{n-1} \end{array}\right),\;\; B = \left(\begin{array}{ccccccc}&&&&&1&0\\&&&&\unicode{x22F0}&\unicode{x22F0}&\\ &&&1&r&&\\ &&1&c_1&&& \\ &\unicode{x22F0}&r&&c_3&&\\ 1&\unicode{x22F0}&&&&\ddots&\\ 0&&&&&&c_n \end{array}\right). \end{align} $$
$$ \begin{align} A = \left(\begin{array}{ccccccc}&&&&&&1\\&&&&&\unicode{x22F0}&\\ &&&&m&&\\ &&&c_0&&& \\ &&m&&c_{2}&&\\ &\unicode{x22F0}&&&&\ddots&\\ 1&&&&&&c_{n-1} \end{array}\right),\;\; B = \left(\begin{array}{ccccccc}&&&&&1&0\\&&&&\unicode{x22F0}&\unicode{x22F0}&\\ &&&1&r&&\\ &&1&c_1&&& \\ &\unicode{x22F0}&r&&c_3&&\\ 1&\unicode{x22F0}&&&&\ddots&\\ 0&&&&&&c_n \end{array}\right). \end{align} $$
Here, the dots on the antidiagonal of A are all
![]() $1$
and the dots on the antidiagonal of B are all
$1$
and the dots on the antidiagonal of B are all
![]() $0$
. We claim that
$0$
. We claim that
![]() $c_i,r$
can be chosen to be integers so that
$c_i,r$
can be chosen to be integers so that
![]() $(-1)^g\det (xA - yB) = f((x,y)\gamma )$
. It is clear that
$(-1)^g\det (xA - yB) = f((x,y)\gamma )$
. It is clear that
![]() $c_0 = b_0$
and
$c_0 = b_0$
and
![]() $2mrc_0 + m^2c_1 = -mb_1$
. Choose
$2mrc_0 + m^2c_1 = -mb_1$
. Choose
![]() $r\in {\mathbb {Z}}$
such that
$r\in {\mathbb {Z}}$
such that
![]() $m\mid 2rc_0+b_{1}$
; this then determines
$m\mid 2rc_0+b_{1}$
; this then determines
![]() $c_{1}$
. It is then not hard to check that the coefficient of
$c_{1}$
. It is then not hard to check that the coefficient of
![]() $x^{n-i}y^i$
in
$x^{n-i}y^i$
in
![]() $(-1)^g\det (xA - yB)$
is of the form
$(-1)^g\det (xA - yB)$
is of the form
![]() $(-1)^ic_i + L(c_0,\ldots ,c_{i-1})$
where L is a linear form with coefficients in
$(-1)^ic_i + L(c_0,\ldots ,c_{i-1})$
where L is a linear form with coefficients in
![]() ${\mathbb {Z}}[r]$
. The existence of integers
${\mathbb {Z}}[r]$
. The existence of integers
![]() $c_2,\ldots ,c_n$
now follows by induction.
$c_2,\ldots ,c_n$
now follows by induction.
Set
![]() $\sigma _m(f)=\sigma _{m,n}(f)$
to be the element
$\sigma _m(f)=\sigma _{m,n}(f)$
to be the element
![]() $(A_f,B_f)$
such that
$(A_f,B_f)$
such that
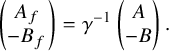 $$ \begin{align*}\begin{pmatrix} A_f \\ -B_f \end{pmatrix} = \gamma^{-1} \begin{pmatrix} A \\ -B \end{pmatrix}.\end{align*} $$
$$ \begin{align*}\begin{pmatrix} A_f \\ -B_f \end{pmatrix} = \gamma^{-1} \begin{pmatrix} A \\ -B \end{pmatrix}.\end{align*} $$
Then
![]() $f_{\sigma _{m}(f)} = f.$
Next, we note that
$f_{\sigma _{m}(f)} = f.$
Next, we note that
![]() $(A,B)$
, and thus,
$(A,B)$
, and thus,
![]() $(A_f,B_f)$
are in
$(A_f,B_f)$
are in
![]() $W_{0}({\mathbb {Z}})$
, and from Lemma 3.3, we obtain that
$W_{0}({\mathbb {Z}})$
, and from Lemma 3.3, we obtain that
![]() $|Q|(A,B) = m$
. Since Q is
$|Q|(A,B) = m$
. Since Q is
![]() $\mathrm {{SL}}_2$
-invariant, we conclude that
$\mathrm {{SL}}_2$
-invariant, we conclude that
We have proven the following theorem.
Theorem 3.7. Let
![]() $m>0$
be a squarefree integer. There exists a map
$m>0$
be a squarefree integer. There exists a map
![]() $\sigma _{m}:{\mathcal {W}}_{m}^{\mathrm {{{(2)}}}}\to W_{0}({\mathbb {Z}})$
such that
$\sigma _{m}:{\mathcal {W}}_{m}^{\mathrm {{{(2)}}}}\to W_{0}({\mathbb {Z}})$
such that
for every
![]() $f\in {\mathcal {W}}_{m}^{\mathrm {{{(2)}}}}$
.
$f\in {\mathcal {W}}_{m}^{\mathrm {{{(2)}}}}$
.
We will later use the image of
![]() $\sigma _{1}$
as a fundamental set for the action of
$\sigma _{1}$
as a fundamental set for the action of
![]() $\mathrm {{SL}}_n({\mathbb {R}})$
on the set of distinguished elements of
$\mathrm {{SL}}_n({\mathbb {R}})$
on the set of distinguished elements of
![]() $W({\mathbb {R}})$
. We now extend the function
$W({\mathbb {R}})$
. We now extend the function
![]() $|Q|$
to the set of distinguished elements of
$|Q|$
to the set of distinguished elements of
![]() $W({\mathbb {Z}})$
having irreducible invariant binary form. Suppose that
$W({\mathbb {Z}})$
having irreducible invariant binary form. Suppose that
![]() $(A,B)$
is a distinguished element of
$(A,B)$
is a distinguished element of
![]() $W({\mathbb {Z}})$
. Then there is a g-dimensional subspace X isotropic with respect to A and B. Let
$W({\mathbb {Z}})$
. Then there is a g-dimensional subspace X isotropic with respect to A and B. Let
![]() $\Lambda = X\cap {\mathbb {Z}}^n$
be the primitive lattice in X. There exists an element
$\Lambda = X\cap {\mathbb {Z}}^n$
be the primitive lattice in X. There exists an element
![]() $\gamma $
in
$\gamma $
in
![]() $\mathrm {{SL}}_n({\mathbb {Z}})$
, unique up to left multiplication by an element in
$\mathrm {{SL}}_n({\mathbb {Z}})$
, unique up to left multiplication by an element in
![]() $G_0({\mathbb {Z}})$
, such that
$G_0({\mathbb {Z}})$
, such that
![]() $\Lambda = \gamma ^t\cdot \,\text {Span}_{\mathbb {Z}}\{e_1,\ldots ,e_g\}$
, where
$\Lambda = \gamma ^t\cdot \,\text {Span}_{\mathbb {Z}}\{e_1,\ldots ,e_g\}$
, where
![]() $e_1,\ldots ,e_n$
is the standard basis of
$e_1,\ldots ,e_n$
is the standard basis of
![]() ${\mathbb {Z}}^n$
. Then
${\mathbb {Z}}^n$
. Then
![]() $\gamma \cdot (A,B)\in W_{0}({\mathbb {Z}})$
, and we can thus define the
$\gamma \cdot (A,B)\in W_{0}({\mathbb {Z}})$
, and we can thus define the
![]() $|Q|$
-invariant on the triple
$|Q|$
-invariant on the triple
![]() $(A,B,\Lambda )$
by
$(A,B,\Lambda )$
by
That is, we complete an integral basis of
![]() $\Lambda $
to an integral basis of
$\Lambda $
to an integral basis of
![]() ${\mathbb {Z}}^n$
with respect to which the pair
${\mathbb {Z}}^n$
with respect to which the pair
![]() $(A',B')$
of Gram matrices for the quadratic forms defined by A and B lies inside
$(A',B')$
of Gram matrices for the quadratic forms defined by A and B lies inside
![]() $W_0({\mathbb {Z}})$
, and we define
$W_0({\mathbb {Z}})$
, and we define
![]() $|Q|(A,B,\Lambda )$
to be
$|Q|(A,B,\Lambda )$
to be
![]() $|Q|(A',B').$
$|Q|(A',B').$
We end with the following result that will be crucial in Section 4.
Proposition 3.8. Let
![]() $n=2g+1$
be an odd integer with
$n=2g+1$
be an odd integer with
![]() $n\geq 3$
. Let m be an odd positive squarefree integer. Let
$n\geq 3$
. Let m be an odd positive squarefree integer. Let
![]() $f(x,y)\in {\mathcal {W}}_{m}^{(2)}$
be an irreducible integral binary n-ic form. Let
$f(x,y)\in {\mathcal {W}}_{m}^{(2)}$
be an irreducible integral binary n-ic form. Let
![]() $(A,B)$
be any element in
$(A,B)$
be any element in
![]() $\mathrm {{SL}}_n({\mathbb {Z}})\cdot \sigma _{m}(f)$
. Then there is a unique primitive g-dimensional lattice
$\mathrm {{SL}}_n({\mathbb {Z}})\cdot \sigma _{m}(f)$
. Then there is a unique primitive g-dimensional lattice
![]() $\Lambda $
that is isotropic with respect to both A and B. Moreover,
$\Lambda $
that is isotropic with respect to both A and B. Moreover,
![]() $|Q|(A,B):=|Q|(A,B,\Lambda )=m$
. In particular, if
$|Q|(A,B):=|Q|(A,B,\Lambda )=m$
. In particular, if
![]() $f(x,y)\in {\mathcal {W}}_{m}^{(2)}\cap {\mathcal {W}}_{m'}^{(2)}$
is irreducible where m and
$f(x,y)\in {\mathcal {W}}_{m}^{(2)}\cap {\mathcal {W}}_{m'}^{(2)}$
is irreducible where m and
![]() $m'$
are distinct odd positive squarefree integers, then
$m'$
are distinct odd positive squarefree integers, then
![]() $\sigma _{m}(f(x,y))$
and
$\sigma _{m}(f(x,y))$
and
![]() $\sigma _{m'}(f(x,y))$
are not
$\sigma _{m'}(f(x,y))$
are not
![]() $\mathrm {{SL}}_{n}({\mathbb {Z}})$
-equivalent.
$\mathrm {{SL}}_{n}({\mathbb {Z}})$
-equivalent.
Proof. Let
![]() $C_f$
denote the smooth hyperelliptic curve
$C_f$
denote the smooth hyperelliptic curve
![]() $z^2=f(x,y)y$
of genus g viewed as a curve in the weighted projective space
$z^2=f(x,y)y$
of genus g viewed as a curve in the weighted projective space
![]() ${\mathbb {P}}(1,1,g+1)$
, and let
${\mathbb {P}}(1,1,g+1)$
, and let
![]() $J_f$
denote its Jacobian. Since
$J_f$
denote its Jacobian. Since
![]() $(A,B)$
is
$(A,B)$
is
![]() $\mathrm {{SL}}_n({\mathbb {Z}})$
-equivalent to
$\mathrm {{SL}}_n({\mathbb {Z}})$
-equivalent to
![]() $\sigma _{m}(f)$
, it follows that
$\sigma _{m}(f)$
, it follows that
![]() $(A,B)$
is distinguished. Thus, the set of common isotropic g-dimensional subspaces of A and B over
$(A,B)$
is distinguished. Thus, the set of common isotropic g-dimensional subspaces of A and B over
![]() ${\mathbb {Q}}$
is in bijection with
${\mathbb {Q}}$
is in bijection with
![]() $J_f[2]({\mathbb {Q}})$
. Since f is irreducible, we have
$J_f[2]({\mathbb {Q}})$
. Since f is irreducible, we have
![]() $J_f[2]({\mathbb {Q}})=1$
. Therefore, there is a unique primitive g-dimensional lattice
$J_f[2]({\mathbb {Q}})=1$
. Therefore, there is a unique primitive g-dimensional lattice
![]() $\Lambda $
which is isotropic with respect to both A and B.
$\Lambda $
which is isotropic with respect to both A and B.
Let
![]() $\gamma \in \mathrm {{SL}}_n({\mathbb {Z}})$
be an element such that
$\gamma \in \mathrm {{SL}}_n({\mathbb {Z}})$
be an element such that
![]() $\gamma (A,B) = \sigma _{m}(f) =: (A_f, B_f)\in W_{0}({\mathbb {Z}})$
. Since we know that
$\gamma (A,B) = \sigma _{m}(f) =: (A_f, B_f)\in W_{0}({\mathbb {Z}})$
. Since we know that
![]() $\text {Span}_{\mathbb {Z}}\{e_1,\ldots ,e_g\}$
is a primitive g-dimensional lattice isotropic with respect to
$\text {Span}_{\mathbb {Z}}\{e_1,\ldots ,e_g\}$
is a primitive g-dimensional lattice isotropic with respect to
![]() $A_f$
and
$A_f$
and
![]() $B_f$
, we see that
$B_f$
, we see that
![]() $\gamma ^t\cdot \,\text {Span}_{\mathbb {Z}}\{e_1,\ldots ,e_g\}$
is a primitive g-dimensional lattice isotropic with respect to A and B. By uniqueness, it follows that
$\gamma ^t\cdot \,\text {Span}_{\mathbb {Z}}\{e_1,\ldots ,e_g\}$
is a primitive g-dimensional lattice isotropic with respect to A and B. By uniqueness, it follows that
![]() $\Lambda = \gamma ^t\cdot \,\text {Span}_{\mathbb {Z}}\{e_1,\ldots ,e_g\}$
, and so by definition,
$\Lambda = \gamma ^t\cdot \,\text {Span}_{\mathbb {Z}}\{e_1,\ldots ,e_g\}$
, and so by definition,
![]() $|Q|(A,B,\Lambda )=|Q|(\sigma _{m}(f))=m$
, where the final equality is Theorem 3.7.
$|Q|(A,B,\Lambda )=|Q|(\sigma _{m}(f))=m$
, where the final equality is Theorem 3.7.
3.5 Embedding
 ${\mathcal {W}}_{m,n}^{(2),\,\mathrm {{gen}}}$
into
${\mathcal {W}}_{m,n}^{(2),\,\mathrm {{gen}}}$
into
 $W_{n+1}({\mathbb {Z}})$
, for n even
$W_{n+1}({\mathbb {Z}})$
, for n even
Suppose now that
![]() $n = 2g+2$
is even with
$n = 2g+2$
is even with
![]() $g\geq 1$
. For an odd squarefree integer
$g\geq 1$
. For an odd squarefree integer
![]() $m>0$
, let
$m>0$
, let
![]() ${\mathcal {W}}_{m,n}^{\mathrm {{{(2)}}}}$
denote the set of integer binary forms having discriminant weakly divisible by
${\mathcal {W}}_{m,n}^{\mathrm {{{(2)}}}}$
denote the set of integer binary forms having discriminant weakly divisible by
![]() $p^2$
for every prime factor p of m. Let
$p^2$
for every prime factor p of m. Let
![]() ${\mathcal {W}}_{m,n}^{(2),\,\mathrm {{gen}}}\subset {\mathcal {W}}_{m,n}^{(2)}$
consist of those
${\mathcal {W}}_{m,n}^{(2),\,\mathrm {{gen}}}\subset {\mathcal {W}}_{m,n}^{(2)}$
consist of those
![]() $f(x,y)$
with
$f(x,y)$
with
![]() $f(0,1)$
coprime to m. Since
$f(0,1)$
coprime to m. Since
![]() $\Delta (xf(x,y)) = \Delta (f(x,y))f(0,1)^2$
, we see that if
$\Delta (xf(x,y)) = \Delta (f(x,y))f(0,1)^2$
, we see that if
![]() $f(x,y)\in {\mathcal {W}}_{m,n}^{(2),\,\mathrm {{gen}}}$
, then
$f(x,y)\in {\mathcal {W}}_{m,n}^{(2),\,\mathrm {{gen}}}$
, then
![]() $xf(x,y)\in {\mathcal {W}}_{m,n+1}^{(2)}$
. We define
$xf(x,y)\in {\mathcal {W}}_{m,n+1}^{(2)}$
. We define
![]() $\sigma _{m,n}:{\mathcal {W}}_{m,n}^{(2),\,\mathrm {{gen}}}\rightarrow W_{n+1}({\mathbb {Z}})$
via
$\sigma _{m,n}:{\mathcal {W}}_{m,n}^{(2),\,\mathrm {{gen}}}\rightarrow W_{n+1}({\mathbb {Z}})$
via
![]() $\sigma _{m,n}(f) = \sigma _{m,n+1}(xf)$
. For the rest of this subsection, we drop subscripts and denote
$\sigma _{m,n}(f) = \sigma _{m,n+1}(xf)$
. For the rest of this subsection, we drop subscripts and denote
![]() $\sigma _{m,n}$
by
$\sigma _{m,n}$
by
![]() $\sigma _m$
,
$\sigma _m$
,
![]() ${\mathcal {W}}_{m,n}^{\mathrm {{{(2)}}},\,\mathrm {{gen}}}$
by
${\mathcal {W}}_{m,n}^{\mathrm {{{(2)}}},\,\mathrm {{gen}}}$
by
![]() ${\mathcal {W}}_m^{\mathrm {{{(2)}}}\,\mathrm {{gen}}}$
, and
${\mathcal {W}}_m^{\mathrm {{{(2)}}}\,\mathrm {{gen}}}$
, and
![]() $W_{n+1}$
by W.
$W_{n+1}$
by W.
We now define the finer q-invariant. Let
![]() $f\in {\mathcal {W}}_{m}^{(2),\,\mathrm {{gen}}}$
and suppose
$f\in {\mathcal {W}}_{m}^{(2),\,\mathrm {{gen}}}$
and suppose
![]() $(A,B) = \sigma _{m}(f)$
. Then B is singular since
$(A,B) = \sigma _{m}(f)$
. Then B is singular since
![]() $xf(x,y)$
has vanishing
$xf(x,y)$
has vanishing
![]() $y^n$
-term. Moreover, since
$y^n$
-term. Moreover, since
![]() $\Delta (xf)\neq 0$
, the kernel of B has dimension exactly
$\Delta (xf)\neq 0$
, the kernel of B has dimension exactly
![]() $1$
and is not isotropic with respect to A (see Lemma 6.4). Fix an integral domain D. Let
$1$
and is not isotropic with respect to A (see Lemma 6.4). Fix an integral domain D. Let
![]() $W_{1}(D)$
be the subset of
$W_{1}(D)$
be the subset of
![]() $W(D)$
consisting of pairs
$W(D)$
consisting of pairs
![]() $(A,B)$
of symmetric
$(A,B)$
of symmetric
![]() $(n+1)\times (n+1)$
matrices satisfying the following conditions:
$(n+1)\times (n+1)$
matrices satisfying the following conditions:
-
(a) The top left
 $(g+1)\times (g+1)$
block of A is
$(g+1)\times (g+1)$
block of A is
 $0$
.
$0$
. -
(b) The top left
 $(g+2)\times (g+2)$
block of B is
$(g+2)\times (g+2)$
block of B is
 $0$
(implying that B is singular).
$0$
(implying that B is singular). -
(c) The kernel of B has dimension exactly
 $1$
(over the fraction field of D) and is not isotropic with respect to A.
$1$
(over the fraction field of D) and is not isotropic with respect to A.
Take any
![]() $(A,B)\in W_{1}(D)$
. Conditions (a) and (c) imply that the first
$(A,B)\in W_{1}(D)$
. Conditions (a) and (c) imply that the first
![]() $g+1$
columns of B are linearly independent over the fraction field of D. Let
$g+1$
columns of B are linearly independent over the fraction field of D. Let
![]() $B'$
denote the top right
$B'$
denote the top right
![]() $(g+1)\times (g+1)$
block of B. Since B is symmetric, we see that
$(g+1)\times (g+1)$
block of B. Since B is symmetric, we see that
![]() $B'$
is nonsingular. It is now easy to see from the definition of the Q-invariant that as polynomials in the coordinates of
$B'$
is nonsingular. It is now easy to see from the definition of the Q-invariant that as polynomials in the coordinates of
![]() $W_{1}(D)$
, we have
$W_{1}(D)$
, we have
We define the quotient to be the q-invariant of
![]() $(A,B)$
:
$(A,B)$
:
Let
![]() $G_1(D)$
denote the subgroup of
$G_1(D)$
denote the subgroup of
![]() $\mathrm {{SL}}_{n+1}(D)$
preserving
$\mathrm {{SL}}_{n+1}(D)$
preserving
![]() $W_{1}(D)$
. Then elements of
$W_{1}(D)$
. Then elements of
![]() $G_1(D)$
have the following block matrix form:
$G_1(D)$
have the following block matrix form:
 $$ \begin{align} \gamma=\left(\begin{array}{ccc}\gamma_1 & 0 & 0\\ n_1 & \gamma_2 & 0\\ n_2 & n_3 & \gamma_3 \end{array}\right)\in\left(\begin{array}{ccc}\mathrm{{GL}}_{g+1} & &\\ M_{1\times (g+1)} & \mathrm{{GL}}_1 &\\ M_{(g+1)\times (g+1)} & M_{(g+1)\times 1} & \mathrm{{GL}}_{g+1} \end{array}\right). \end{align} $$
$$ \begin{align} \gamma=\left(\begin{array}{ccc}\gamma_1 & 0 & 0\\ n_1 & \gamma_2 & 0\\ n_2 & n_3 & \gamma_3 \end{array}\right)\in\left(\begin{array}{ccc}\mathrm{{GL}}_{g+1} & &\\ M_{1\times (g+1)} & \mathrm{{GL}}_1 &\\ M_{(g+1)\times (g+1)} & M_{(g+1)\times 1} & \mathrm{{GL}}_{g+1} \end{array}\right). \end{align} $$
It is easy to check that for any
![]() $(A,B)\in W_{1}(D)$
,
$(A,B)\in W_{1}(D)$
,
We now consider the situation over
![]() ${\mathbb {Z}}$
. Let
${\mathbb {Z}}$
. Let
![]() $(A,B)\in W({\mathbb {Z}})$
be a distinguished element having nonzero discriminant such that B is singular. Let X denote a common isotropic
$(A,B)\in W({\mathbb {Z}})$
be a distinguished element having nonzero discriminant such that B is singular. Let X denote a common isotropic
![]() $(g+1)$
-dimiensional subspace of A and B. We know that the kernel
$(g+1)$
-dimiensional subspace of A and B. We know that the kernel
![]() $\langle v\rangle $
of B has trivial intersection with X. Denote the span of X and v by
$\langle v\rangle $
of B has trivial intersection with X. Denote the span of X and v by
![]() $X'$
, which is a
$X'$
, which is a
![]() $(g+2)$
-dimensional subspace containing X that is isotropic with respect to B. Let
$(g+2)$
-dimensional subspace containing X that is isotropic with respect to B. Let
![]() $\Lambda = X\cap {\mathbb {Z}}^{n+1}$
and
$\Lambda = X\cap {\mathbb {Z}}^{n+1}$
and
![]() $\Lambda ' = X'\cap {\mathbb {Z}}^{n+1}$
be the primitive lattices in X and
$\Lambda ' = X'\cap {\mathbb {Z}}^{n+1}$
be the primitive lattices in X and
![]() $X'$
, respectively. There exists an element
$X'$
, respectively. There exists an element
![]() $\gamma $
in
$\gamma $
in
![]() $\mathrm {{SL}}_{n+1}({\mathbb {Z}})$
, unique up to left multiplication by an element in
$\mathrm {{SL}}_{n+1}({\mathbb {Z}})$
, unique up to left multiplication by an element in
![]() $G_1({\mathbb {Z}})$
, such that
$G_1({\mathbb {Z}})$
, such that
![]() $\Lambda = \gamma ^t.\,\text {Span}_{\mathbb {Z}}\{e_1,\ldots ,e_{g+1}\}$
and
$\Lambda = \gamma ^t.\,\text {Span}_{\mathbb {Z}}\{e_1,\ldots ,e_{g+1}\}$
and
![]() $\Lambda ' = \gamma ^t.\,\text {Span}_{\mathbb {Z}}\{e_1,\ldots ,e_{g+2}\}$
. Then
$\Lambda ' = \gamma ^t.\,\text {Span}_{\mathbb {Z}}\{e_1,\ldots ,e_{g+2}\}$
. Then
![]() $\gamma (A,B)\in W_{1}({\mathbb {Z}})$
, and we can thus define the
$\gamma (A,B)\in W_{1}({\mathbb {Z}})$
, and we can thus define the
![]() $|q|$
-invariant for the quadruple
$|q|$
-invariant for the quadruple
![]() $(A,B,\Lambda ,\Lambda ')$
by
$(A,B,\Lambda ,\Lambda ')$
by
In other words, we complete an integral basis
![]() $\{v_1,\ldots ,v_{g+1}\}$
of
$\{v_1,\ldots ,v_{g+1}\}$
of
![]() $\Lambda $
to an integral basis
$\Lambda $
to an integral basis
![]() $\{v_1,\ldots ,v_{n+1}\}$
of
$\{v_1,\ldots ,v_{n+1}\}$
of
![]() ${\mathbb {Z}}^{n+1}$
such that
${\mathbb {Z}}^{n+1}$
such that
![]() $\{v_1,\ldots ,v_{g+2}\}$
forms an integral basis of
$\{v_1,\ldots ,v_{g+2}\}$
forms an integral basis of
![]() $\Lambda '$
. When expressed in this basis, the pair
$\Lambda '$
. When expressed in this basis, the pair
![]() $(A',B')$
of Gram matrices for the quadratic forms defined by A and B lies in
$(A',B')$
of Gram matrices for the quadratic forms defined by A and B lies in
![]() $W_{1}({\mathbb {Z}})$
and we define
$W_{1}({\mathbb {Z}})$
and we define
![]() $|q|(A,B,\Lambda ,\Lambda ') := |q|(A',B').$
$|q|(A,B,\Lambda ,\Lambda ') := |q|(A',B').$
Finally, we compute the
![]() $|Q|$
- and
$|Q|$
- and
![]() $|q|$
-invariants of
$|q|$
-invariants of
![]() $\sigma _{m}(f(x,y))$
, where
$\sigma _{m}(f(x,y))$
, where
![]() $f(x,y)\in {\mathcal {W}}_{m}^{(2),\,\mathrm {{gen}}}$
is irreducible.
$f(x,y)\in {\mathcal {W}}_{m}^{(2),\,\mathrm {{gen}}}$
is irreducible.
Proposition 3.9. Let
![]() $n=2g+2$
with
$n=2g+2$
with
![]() $g\geq 1$
. Let m be an odd positive squarefree integer. Let
$g\geq 1$
. Let m be an odd positive squarefree integer. Let
![]() $f(x,y)\in {\mathcal {W}}_{m}^{(2),\,\mathrm {{gen}}}$
be irreducible. Let
$f(x,y)\in {\mathcal {W}}_{m}^{(2),\,\mathrm {{gen}}}$
be irreducible. Let
![]() $(A,B)$
be any element in
$(A,B)$
be any element in
![]() $\mathrm {{SL}}_{n+1}({\mathbb {Z}})\cdot \sigma _{m}(f(x,y))$
. Let
$\mathrm {{SL}}_{n+1}({\mathbb {Z}})\cdot \sigma _{m}(f(x,y))$
. Let
![]() $\Lambda $
be a
$\Lambda $
be a
![]() $(g+1)$
-dimensional primitive lattice contained in a
$(g+1)$
-dimensional primitive lattice contained in a
![]() $(g+2)$
-dimensional primitive lattice
$(g+2)$
-dimensional primitive lattice
![]() $\Lambda '$
such that
$\Lambda '$
such that
![]() $\Lambda $
is isotropic with respect to A and
$\Lambda $
is isotropic with respect to A and
![]() $\Lambda '$
is isotropic with respect to B. Then
$\Lambda '$
is isotropic with respect to B. Then
![]() $|Q|(A,B,\Lambda )$
is either m or
$|Q|(A,B,\Lambda )$
is either m or
![]() $|f(0,1)|m$
, and
$|f(0,1)|m$
, and
![]() $|q|(A,B) := |q|(A,B,\Lambda ,\Lambda ') = m$
, independent of
$|q|(A,B) := |q|(A,B,\Lambda ,\Lambda ') = m$
, independent of
![]() $(\Lambda ,\Lambda ')$
. In particular, if
$(\Lambda ,\Lambda ')$
. In particular, if
![]() $f(x,y)\in {\mathcal {W}}_{m}^{(2),\,\mathrm {{gen}}}\cap {\mathcal {W}}_{m'}^{(2),\,\mathrm {{gen}}}$
is irreducible where m and
$f(x,y)\in {\mathcal {W}}_{m}^{(2),\,\mathrm {{gen}}}\cap {\mathcal {W}}_{m'}^{(2),\,\mathrm {{gen}}}$
is irreducible where m and
![]() $m'$
are distinct odd positive squarefree integers, then
$m'$
are distinct odd positive squarefree integers, then
![]() $\sigma _{m}(f(x,y))$
and
$\sigma _{m}(f(x,y))$
and
![]() $\sigma _{m'}(f(x,y))$
are not
$\sigma _{m'}(f(x,y))$
are not
![]() $\mathrm {{SL}}_{n+1}({\mathbb {Z}})$
-equivalent.
$\mathrm {{SL}}_{n+1}({\mathbb {Z}})$
-equivalent.
Proof. The size of
![]() $J_f[2]({\mathbb {Q}})$
is
$J_f[2]({\mathbb {Q}})$
is
![]() $2$
since
$2$
since
![]() $xf(x,y)$
has a unique even degree factor (namely,
$xf(x,y)$
has a unique even degree factor (namely,
![]() $f(x,y)$
) over
$f(x,y)$
) over
![]() ${\mathbb {Q}}$
. Therefore, the pair
${\mathbb {Q}}$
. Therefore, the pair
![]() $(A,B)$
has two
$(A,B)$
has two
![]() $(g+1)$
-dimensional common isotropic subspaces
$(g+1)$
-dimensional common isotropic subspaces
![]() $X_1$
and
$X_1$
and
![]() $X_2$
over
$X_2$
over
![]() ${\mathbb {Q}}$
. Let
${\mathbb {Q}}$
. Let
![]() $\Lambda _1$
and
$\Lambda _1$
and
![]() $\Lambda _2$
denote the corresponding primitive lattices contained in
$\Lambda _2$
denote the corresponding primitive lattices contained in
![]() $X_1$
and
$X_1$
and
![]() $X_2$
. The unique
$X_2$
. The unique
![]() $(g+2)$
-dimensional subspace
$(g+2)$
-dimensional subspace
![]() $X_1'$
(resp.,
$X_1'$
(resp.,
![]() $X_2'$
) isotropic with respect to B and containing
$X_2'$
) isotropic with respect to B and containing
![]() $X_1$
(resp.,
$X_1$
(resp.,
![]() $X_2$
) is the span of
$X_2$
) is the span of
![]() $X_1$
(resp.,
$X_1$
(resp.,
![]() $X_2$
) with the kernel of B. Let
$X_2$
) with the kernel of B. Let
![]() $\Lambda ^{\prime }_1$
and
$\Lambda ^{\prime }_1$
and
![]() $\Lambda _2'$
denote the primitive lattices contained in
$\Lambda _2'$
denote the primitive lattices contained in
![]() $X_1'$
and
$X_1'$
and
![]() $X_2'$
. We compute the
$X_2'$
. We compute the
![]() $|Q|$
- and
$|Q|$
- and
![]() $|q|$
-invariants associated to these lattices.
$|q|$
-invariants associated to these lattices.
We may assume that
![]() $(A,B)=\sigma _{m}(f)$
since the action of
$(A,B)=\sigma _{m}(f)$
since the action of
![]() $\mathrm {{SL}}_{n+1}({\mathbb {Z}})$
does not change the
$\mathrm {{SL}}_{n+1}({\mathbb {Z}})$
does not change the
![]() $|Q|$
- or
$|Q|$
- or
![]() $|q|$
invariants. Since
$|q|$
invariants. Since
![]() $|Q|$
is
$|Q|$
is
![]() $\mathrm {{SL}}_2$
-invariant, and
$\mathrm {{SL}}_2$
-invariant, and
![]() $|q|$
remains unchanged when we add a multiple of B to A, we may also assume that
$|q|$
remains unchanged when we add a multiple of B to A, we may also assume that
and so
 $$ \begin{align*} A = \left(\begin{array}{ccccccc}&&&&&&1\\&&&&&\unicode{x22F0}&\\ &&&&m&&\\ &&&c_0&&& \\ &&m&&c_{2}&&\\ &\unicode{x22F0}&&&&\ddots&\\ 1&&&&&&c_n \end{array}\right),\;\; B = \left(\begin{array}{ccccccc}&&&&&1&0\\&&&&\unicode{x22F0}&\unicode{x22F0}&\\ &&&1&r&&\\ &&1&c_1&&& \\ &\unicode{x22F0}&r&&c_3&&\\ 1&\unicode{x22F0}&&&&\ddots&\\ 0&&&&&&c_{n+1} \end{array}\right). \end{align*} $$
$$ \begin{align*} A = \left(\begin{array}{ccccccc}&&&&&&1\\&&&&&\unicode{x22F0}&\\ &&&&m&&\\ &&&c_0&&& \\ &&m&&c_{2}&&\\ &\unicode{x22F0}&&&&\ddots&\\ 1&&&&&&c_n \end{array}\right),\;\; B = \left(\begin{array}{ccccccc}&&&&&1&0\\&&&&\unicode{x22F0}&\unicode{x22F0}&\\ &&&1&r&&\\ &&1&c_1&&& \\ &\unicode{x22F0}&r&&c_3&&\\ 1&\unicode{x22F0}&&&&\ddots&\\ 0&&&&&&c_{n+1} \end{array}\right). \end{align*} $$
Comparing the
![]() $y^{n+1}$
- and the
$y^{n+1}$
- and the
![]() $xy^{n}$
-coefficients, we have
$xy^{n}$
-coefficients, we have
![]() $c_{n+1} = 0$
and
$c_{n+1} = 0$
and
![]() $c_{n}=b_{n}$
.
$c_{n}=b_{n}$
.
Let
![]() $\langle \,,\rangle _A$
and
$\langle \,,\rangle _A$
and
![]() $\langle \,,\rangle _B$
denote the quadratic forms corresponding to A and B. Let
$\langle \,,\rangle _B$
denote the quadratic forms corresponding to A and B. Let
![]() $e_1,\ldots ,e_{n+1}$
be the standard basis on
$e_1,\ldots ,e_{n+1}$
be the standard basis on
![]() ${\mathbb {Z}}^{n+1}$
. Since
${\mathbb {Z}}^{n+1}$
. Since
![]() $c_{n+1}=0$
, the vector
$c_{n+1}=0$
, the vector
![]() $e_{n+1}$
spans the kernel of B. We may take the subspace spanned by
$e_{n+1}$
spans the kernel of B. We may take the subspace spanned by
![]() $e_1,\ldots ,e_{g+1}$
as
$e_1,\ldots ,e_{g+1}$
as
![]() $X_1$
. Then by construction,
$X_1$
. Then by construction,
![]() $|Q|(A,B,\Lambda _1) = m$
. When expressed in terms of the ordered integral basis
$|Q|(A,B,\Lambda _1) = m$
. When expressed in terms of the ordered integral basis
![]() $\{e_1,\ldots ,e_{g+1},e_n,e_{g+2},\ldots ,e_{n-1}\}$
, the top right
$\{e_1,\ldots ,e_{g+1},e_n,e_{g+2},\ldots ,e_{n-1}\}$
, the top right
![]() $(g+1)\times (g+1)$
block of B has
$(g+1)\times (g+1)$
block of B has
![]() $1$
’s on the antidiagonal and
$1$
’s on the antidiagonal and
![]() $0$
’s above the antidiagonal, and so has determinant
$0$
’s above the antidiagonal, and so has determinant
![]() $\pm 1$
. Hence,
$\pm 1$
. Hence,
![]() $|q|(A,B,\Lambda _1,\Lambda _1') = m$
.
$|q|(A,B,\Lambda _1,\Lambda _1') = m$
.
The second common isotropic
![]() $(g+1)$
-dimensional subspace
$(g+1)$
-dimensional subspace
![]() $X_2$
is the reflection of
$X_2$
is the reflection of
![]() $X_1$
in the hyperplane perpendicular to
$X_1$
in the hyperplane perpendicular to
![]() $e_{n+1}$
with respect to
$e_{n+1}$
with respect to
![]() $\langle \,,\rangle _A$
. That is,
$\langle \,,\rangle _A$
. That is,
 $$ \begin{align*} X_2 &= \mathrm{Span}_{\mathbb{Q}}\Big\{e_1 - \frac{2\langle e_1,e_{n+1}\rangle_A}{\langle e_{n+1},e_{n+1}\rangle_A}e_{n+1},\ldots,e_{g+1} - \frac{2\langle e_{g+1},e_{n+1}\rangle_A}{\langle e_{n+1},e_{n+1}\rangle_A}e_{n+1}\Big\}\\ &= \mathrm{Span}_{\mathbb{Q}}\Big\{e_1 - \frac{2}{b_n}e_{n+1},e_2,e_3,\ldots,e_{g+1}\Big\}. \end{align*} $$
$$ \begin{align*} X_2 &= \mathrm{Span}_{\mathbb{Q}}\Big\{e_1 - \frac{2\langle e_1,e_{n+1}\rangle_A}{\langle e_{n+1},e_{n+1}\rangle_A}e_{n+1},\ldots,e_{g+1} - \frac{2\langle e_{g+1},e_{n+1}\rangle_A}{\langle e_{n+1},e_{n+1}\rangle_A}e_{n+1}\Big\}\\ &= \mathrm{Span}_{\mathbb{Q}}\Big\{e_1 - \frac{2}{b_n}e_{n+1},e_2,e_3,\ldots,e_{g+1}\Big\}. \end{align*} $$
Suppose first that
![]() $b_n$
is odd. Then we have the following integral basis for
$b_n$
is odd. Then we have the following integral basis for
![]() ${\mathbb {Z}}^{n+1}$
:
${\mathbb {Z}}^{n+1}$
:
In terms of this basis, the top right
![]() $(g+1)\times (g+2)$
blocks of A and B have the following form:
$(g+1)\times (g+2)$
blocks of A and B have the following form:
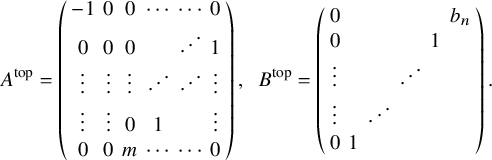 $$ \begin{align}A^{\mathrm{{top}}} = \left(\begin{array}{cccccc} -1&0&0&\cdots&\cdots&0\\0&0&0&&\unicode{x22F0}&1\\ \vdots&\vdots&\vdots&\unicode{x22F0}&\unicode{x22F0}&\vdots\\ \vdots&\vdots&0&1&&\vdots \\ 0&0&m&\cdots&\cdots&0\end{array}\right),\;\; B^{\mathrm{{top}}} = \left(\begin{array}{cccccc}0&&&&&b_{n}\\0&&&&1&\\ \vdots&&&\unicode{x22F0}&&\\ \vdots&&\unicode{x22F0}&&& \\ 0&1&&&&\end{array}\right). \end{align} $$
$$ \begin{align}A^{\mathrm{{top}}} = \left(\begin{array}{cccccc} -1&0&0&\cdots&\cdots&0\\0&0&0&&\unicode{x22F0}&1\\ \vdots&\vdots&\vdots&\unicode{x22F0}&\unicode{x22F0}&\vdots\\ \vdots&\vdots&0&1&&\vdots \\ 0&0&m&\cdots&\cdots&0\end{array}\right),\;\; B^{\mathrm{{top}}} = \left(\begin{array}{cccccc}0&&&&&b_{n}\\0&&&&1&\\ \vdots&&&\unicode{x22F0}&&\\ \vdots&&\unicode{x22F0}&&& \\ 0&1&&&&\end{array}\right). \end{align} $$
It is then easy to check that
![]() $|Q|(A,B,\Lambda _2) = |b_{n}|m$
and
$|Q|(A,B,\Lambda _2) = |b_{n}|m$
and
![]() $|q|(A,B,\Lambda _2,\Lambda _2') = m$
.
$|q|(A,B,\Lambda _2,\Lambda _2') = m$
.
When
![]() $b_{n}$
is even, we have the following integral basis:
$b_{n}$
is even, we have the following integral basis:
In terms of this basis, the top right
![]() $(g+1)\times (g+2)$
blocks of A and B have the same form as in (13). Hence, the
$(g+1)\times (g+2)$
blocks of A and B have the same form as in (13). Hence, the
![]() $|Q|$
- and
$|Q|$
- and
![]() $|q|$
-invariants are as stated in the proposition.
$|q|$
-invariants are as stated in the proposition.
4 A uniformity estimate for odd degree polynomials
Throughout this section, we fix an odd integer
![]() $n=2g+1$
with
$n=2g+1$
with
![]() $g\geq 1$
. Our goal is to prove Theorem 5(b) by obtaining a bound on the number of integral binary n-ic forms having bounded height and discriminant weakly divisible by the square of a large squarefree integer.
$g\geq 1$
. Our goal is to prove Theorem 5(b) by obtaining a bound on the number of integral binary n-ic forms having bounded height and discriminant weakly divisible by the square of a large squarefree integer.
Let
![]() $m>0$
be an odd squarefree integer. Recall that we defined a map
$m>0$
be an odd squarefree integer. Recall that we defined a map
![]() $\sigma _m:{\mathcal {W}}^{(2)}_m\to W_0({\mathbb {Z}})$
in Theorem 3.7 with the following two properties:
$\sigma _m:{\mathcal {W}}^{(2)}_m\to W_0({\mathbb {Z}})$
in Theorem 3.7 with the following two properties:
![]() $f_{\sigma _m(f)}=f$
for every
$f_{\sigma _m(f)}=f$
for every
![]() $f\in {\mathcal {W}}^{(2)}_m$
, and
$f\in {\mathcal {W}}^{(2)}_m$
, and
![]() $|Q|(\sigma _m(f))=m$
. Moreover, in Proposition 3.8, we proved that when
$|Q|(\sigma _m(f))=m$
. Moreover, in Proposition 3.8, we proved that when
![]() $f\in {\mathcal {W}}_m^{(2)}$
is irreducible, it is possible to naturally extend the definition of the
$f\in {\mathcal {W}}_m^{(2)}$
is irreducible, it is possible to naturally extend the definition of the
![]() $|Q|$
-invariant to the set
$|Q|$
-invariant to the set
![]() $\mathrm {{SL}}_n({\mathbb {Z}})\cdot \sigma _m(f)$
.
$\mathrm {{SL}}_n({\mathbb {Z}})\cdot \sigma _m(f)$
.
Let
![]() $W({\mathbb {Z}})^{\mathrm {{dist}}}$
denote the set of distinguished elements in
$W({\mathbb {Z}})^{\mathrm {{dist}}}$
denote the set of distinguished elements in
![]() $W({\mathbb {Z}})$
, and for any set
$W({\mathbb {Z}})$
, and for any set
![]() $L\subset W({\mathbb {Z}})$
, let
$L\subset W({\mathbb {Z}})$
, let
![]() $L^{\mathrm {{irr}}}$
denote the set of elements
$L^{\mathrm {{irr}}}$
denote the set of elements
![]() $w\in L$
such that
$w\in L$
such that
![]() $f_w$
is irreducible. There is a natural extension of the
$f_w$
is irreducible. There is a natural extension of the
![]() $|Q|$
-invariant to the set
$|Q|$
-invariant to the set
![]() $W({\mathbb {Z}})^{\mathrm {{dist}},\mathrm {{irr}}}$
. For a positive real number M and any set
$W({\mathbb {Z}})^{\mathrm {{dist}},\mathrm {{irr}}}$
. For a positive real number M and any set
![]() $S\subset W({\mathbb {Z}})^{\mathrm {{dist}},\mathrm {{irr}}}$
, let
$S\subset W({\mathbb {Z}})^{\mathrm {{dist}},\mathrm {{irr}}}$
, let
![]() $S_{|Q|>M}$
denote the set of elements
$S_{|Q|>M}$
denote the set of elements
![]() $w\in S$
with
$w\in S$
with
![]() $|Q(w)|>M$
. By [Reference Kuba22, Theorem 1], the number of reducible elements
$|Q(w)|>M$
. By [Reference Kuba22, Theorem 1], the number of reducible elements
![]() $f\in V({\mathbb {Z}})$
with
$f\in V({\mathbb {Z}})$
with
![]() $H(f)<X$
is
$H(f)<X$
is
![]() $O(X^n)$
. Hence, we have the bound
$O(X^n)$
. Hence, we have the bound
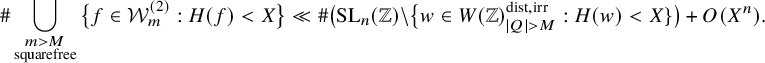 $$ \begin{align} \#\bigcup_{\substack{m>M\\\mathrm{squarefree}}}\big\{f\in{\mathcal{W}}_m^{(2)}:H(f)<X\big\} \ll \#\big(\mathrm{{SL}}_n({\mathbb{Z}})\backslash \big\{w\in W({\mathbb{Z}})^{\mathrm{{dist}},\mathrm{{irr}}}_{|Q|>M}:H(w)<X\}\big)+O(X^{n}). \end{align} $$
$$ \begin{align} \#\bigcup_{\substack{m>M\\\mathrm{squarefree}}}\big\{f\in{\mathcal{W}}_m^{(2)}:H(f)<X\big\} \ll \#\big(\mathrm{{SL}}_n({\mathbb{Z}})\backslash \big\{w\in W({\mathbb{Z}})^{\mathrm{{dist}},\mathrm{{irr}}}_{|Q|>M}:H(w)<X\}\big)+O(X^{n}). \end{align} $$
In this section, we obtain an upper bound on the number of
![]() $\mathrm {{SL}}_n({\mathbb {Z}})$
-orbits on
$\mathrm {{SL}}_n({\mathbb {Z}})$
-orbits on
![]() $W({\mathbb {Z}})^{\mathrm {{dist}},\mathrm {{irr}}}_{|Q|>M}$
with height bounded by X. First, in §4.1, we lay out the reduction theory necessary to express the number of such orbits in terms of the counts of lattice points in certain bounded regions. Then in §4.2, we partition these regions into three parts, the main body, the shallow cusp and the deep cusp. We prove the desired estimate for each of these parts, thereby obtaining Theorem 5(b).
$W({\mathbb {Z}})^{\mathrm {{dist}},\mathrm {{irr}}}_{|Q|>M}$
with height bounded by X. First, in §4.1, we lay out the reduction theory necessary to express the number of such orbits in terms of the counts of lattice points in certain bounded regions. Then in §4.2, we partition these regions into three parts, the main body, the shallow cusp and the deep cusp. We prove the desired estimate for each of these parts, thereby obtaining Theorem 5(b).
4.1 Reduction theory and averaging over fundamental domains
Recall that the Iwasawa decomposition of
![]() $\mathrm {{SL}}_n({\mathbb {R}})$
is given by
$\mathrm {{SL}}_n({\mathbb {R}})$
is given by
![]() $ \mathrm {{SL}}_n({\mathbb {R}})=NTK, $
where N is the group of unipotent lower triangular matrices in
$ \mathrm {{SL}}_n({\mathbb {R}})=NTK, $
where N is the group of unipotent lower triangular matrices in
![]() $\mathrm {{SL}}_n({\mathbb {R}})$
,
$\mathrm {{SL}}_n({\mathbb {R}})$
,
![]() $K=\mathrm {{SO}}(n)$
is a maximal compact subgroup of
$K=\mathrm {{SO}}(n)$
is a maximal compact subgroup of
![]() $\mathrm {{SL}}_n({\mathbb {R}})$
, and T is the split torus of
$\mathrm {{SL}}_n({\mathbb {R}})$
, and T is the split torus of
![]() $\mathrm {{SL}}_n({\mathbb {R}})$
consisting of
$\mathrm {{SL}}_n({\mathbb {R}})$
consisting of
![]() $n\times n$
diagonal matrices with positive diagonal entries and determinant
$n\times n$
diagonal matrices with positive diagonal entries and determinant
![]() $1$
. We denote elements in T by
$1$
. We denote elements in T by
![]() $s=\mathrm {{diag}}(t_1^{-1},t_2^{-1},\ldots ,t_n^{-1})$
, where
$s=\mathrm {{diag}}(t_1^{-1},t_2^{-1},\ldots ,t_n^{-1})$
, where
![]() $t_i>0$
for
$t_i>0$
for
![]() $1\leq 1\leq n$
and
$1\leq 1\leq n$
and
![]() $t_1t_2\cdots t_n=1$
. It will be convenient to make the following change of variables. For
$t_1t_2\cdots t_n=1$
. It will be convenient to make the following change of variables. For
![]() $1\leq i\leq n-1$
, set
$1\leq i\leq n-1$
, set
![]() $s_i$
to be
$s_i$
to be
 $$ \begin{align*} s_i=(t_i/t_{i+1})^{1/n},\text{ which implies }\; t_i=\prod_{k=1}^{i-1}s_k^{-k}\prod_{k=i}^{n-1}s_k^{n-k} \end{align*} $$
$$ \begin{align*} s_i=(t_i/t_{i+1})^{1/n},\text{ which implies }\; t_i=\prod_{k=1}^{i-1}s_k^{-k}\prod_{k=i}^{n-1}s_k^{n-k} \end{align*} $$
for
![]() $1\leq i<n$
. The Haar measure of
$1\leq i<n$
. The Haar measure of
![]() $G({\mathbb {R}})$
in these coordinates is then given by
$G({\mathbb {R}})$
in these coordinates is then given by
 $$ \begin{align*}dg=dn\delta(s)d^\times s dk, \;\;\;\;\;\text{where}\;\;\;\;\; \delta(s)= \prod_{1\leq i < j\leq n}\frac{t_j}{t_i} = \prod_{k=1}^{n-1}s_k^{-nk(n-k)},\end{align*} $$
$$ \begin{align*}dg=dn\delta(s)d^\times s dk, \;\;\;\;\;\text{where}\;\;\;\;\; \delta(s)= \prod_{1\leq i < j\leq n}\frac{t_j}{t_i} = \prod_{k=1}^{n-1}s_k^{-nk(n-k)},\end{align*} $$
![]() $dn$
and
$dn$
and
![]() $dk$
are Haar measures on N and K, respectively, and
$dk$
are Haar measures on N and K, respectively, and
![]() $d^\times s=\prod _{i=1}^{n-1}s_i^{-1}ds_i$
.
$d^\times s=\prod _{i=1}^{n-1}s_i^{-1}ds_i$
.
We denote the coordinates on W by
![]() $a_{ij},b_{ij}$
for
$a_{ij},b_{ij}$
for
![]() $1\leq i\leq j\leq n$
. These coordinates are eigenvectors for the action of T on the dual
$1\leq i\leq j\leq n$
. These coordinates are eigenvectors for the action of T on the dual
![]() $W^*$
of W. Denote the T-weight of a coordinate
$W^*$
of W. Denote the T-weight of a coordinate
![]() $\alpha $
on W, or more generally a product
$\alpha $
on W, or more generally a product
![]() $\alpha $
of powers of such coordinates, by
$\alpha $
of powers of such coordinates, by
![]() $w(\alpha )$
. Then
$w(\alpha )$
. Then
![]() $w(a_{ij}) = w(b_{ij}) = t_i^{-1}t_j^{-1}.$
It will be useful in what follows to compute the weight of the Q-invariant, which is a homogeneous polynomial of degree
$w(a_{ij}) = w(b_{ij}) = t_i^{-1}t_j^{-1}.$
It will be useful in what follows to compute the weight of the Q-invariant, which is a homogeneous polynomial of degree
![]() $g(g+1)$
in the coordinates of
$g(g+1)$
in the coordinates of
![]() $W_0$
. We view the torus T as sitting inside
$W_0$
. We view the torus T as sitting inside
![]() $G_0$
. Then by (5), we have
$G_0$
. Then by (5), we have
 $$ \begin{align} w(Q)=\prod_{k=1}^gt_k^{-1}. \end{align} $$
$$ \begin{align} w(Q)=\prod_{k=1}^gt_k^{-1}. \end{align} $$
Let
![]() ${\mathcal {F}}$
be a fundamental set for the action of
${\mathcal {F}}$
be a fundamental set for the action of
![]() $\mathrm {{SL}}_n({\mathbb {Z}})$
on
$\mathrm {{SL}}_n({\mathbb {Z}})$
on
![]() $\mathrm {{SL}}_n({\mathbb {R}})$
that is contained in a Siegel set (i.e., contained in
$\mathrm {{SL}}_n({\mathbb {R}})$
that is contained in a Siegel set (i.e., contained in
![]() $N'T'K$
, where
$N'T'K$
, where
![]() $N'$
is a set consisting of elements in N whose coefficients are absolutely bounded and
$N'$
is a set consisting of elements in N whose coefficients are absolutely bounded and
![]() $T'\subset T$
consists of elements in
$T'\subset T$
consists of elements in
![]() $s\in T$
with
$s\in T$
with
![]() $s_i\geq c$
for some positive constant c). Let
$s_i\geq c$
for some positive constant c). Let
![]() ${\mathcal {W}}(1)$
denote the subset of real binary n-ic forms of height bounded by
${\mathcal {W}}(1)$
denote the subset of real binary n-ic forms of height bounded by
![]() $1$
and let
$1$
and let
![]() $R' = \sigma _1({\mathcal {W}}(1))$
, where
$R' = \sigma _1({\mathcal {W}}(1))$
, where
![]() $\sigma _1$
is as in §3.4. Set
$\sigma _1$
is as in §3.4. Set
![]() $R:={\mathbb {R}}_{>0}\cdot R'$
, and note that every distinguished element of
$R:={\mathbb {R}}_{>0}\cdot R'$
, and note that every distinguished element of
![]() $W({\mathbb {R}})$
is
$W({\mathbb {R}})$
is
![]() $\mathrm {{SL}}_n({\mathbb {R}})$
-equivalent to some element in R.
$\mathrm {{SL}}_n({\mathbb {R}})$
-equivalent to some element in R.
Let
![]() $H_0$
be a nonempty open bounded left K-invariant set in
$H_0$
be a nonempty open bounded left K-invariant set in
![]() $\mathrm {{SL}}_n({\mathbb {R}})$
. Denote the set
$\mathrm {{SL}}_n({\mathbb {R}})$
. Denote the set
![]() $H_0\cdot R'$
by
$H_0\cdot R'$
by
![]() ${\mathcal {B}}_1$
. Then
${\mathcal {B}}_1$
. Then
![]() ${\mathcal {B}}_1$
is an absolutely bounded set in
${\mathcal {B}}_1$
is an absolutely bounded set in
![]() $W({\mathbb {R}})$
. Let
$W({\mathbb {R}})$
. Let
![]() ${\mathcal {L}}$
be any
${\mathcal {L}}$
be any
![]() $\mathrm {{SL}}_n({\mathbb {Z}})$
-invariant subset of
$\mathrm {{SL}}_n({\mathbb {Z}})$
-invariant subset of
![]() $W({\mathbb {Z}})$
consisting of elements that are distinguished over
$W({\mathbb {Z}})$
consisting of elements that are distinguished over
![]() ${\mathbb {R}}$
, and denote the set of elements in
${\mathbb {R}}$
, and denote the set of elements in
![]() ${\mathcal {L}}$
with height less than X by
${\mathcal {L}}$
with height less than X by
![]() ${\mathcal {L}}_X$
. Throughout this section, let
${\mathcal {L}}_X$
. Throughout this section, let
![]() $Y=X^{1/n}$
. Then the averaging method as described in [Reference Bhargava and Shankar10, §2.3] yields the bound
$Y=X^{1/n}$
. Then the averaging method as described in [Reference Bhargava and Shankar10, §2.3] yields the bound
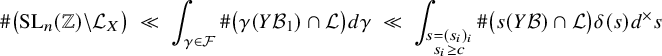 $$ \begin{align} \#\big(\mathrm{{SL}}_n({\mathbb{Z}})\backslash{\mathcal{L}}_X\big) \;\ll\; \int_{\gamma\in{\mathcal{F}}} \#\big(\gamma (Y{\mathcal{B}}_1)\cap {\mathcal{L}}\big)d\gamma \;\ll\; \int_{\substack{s=(s_i)_i\\ s_i\geq c}} \#\big(s (Y{\mathcal{B}})\cap{\mathcal{L}}\big)\delta(s)d^\times s \end{align} $$
$$ \begin{align} \#\big(\mathrm{{SL}}_n({\mathbb{Z}})\backslash{\mathcal{L}}_X\big) \;\ll\; \int_{\gamma\in{\mathcal{F}}} \#\big(\gamma (Y{\mathcal{B}}_1)\cap {\mathcal{L}}\big)d\gamma \;\ll\; \int_{\substack{s=(s_i)_i\\ s_i\geq c}} \#\big(s (Y{\mathcal{B}})\cap{\mathcal{L}}\big)\delta(s)d^\times s \end{align} $$
for some absolutely bounded open set
![]() ${\mathcal {B}}$
containing
${\mathcal {B}}$
containing
![]() ${\mathcal {B}}_1$
.
${\mathcal {B}}_1$
.
We denote the second integral on the right-hand side of (16) by
![]() ${\mathcal {I}}_X({\mathcal {L}})$
, and break it up into an integral over the main body, the shallow cusp and the deep cusp. We define the main body to be the range of the integral where
${\mathcal {I}}_X({\mathcal {L}})$
, and break it up into an integral over the main body, the shallow cusp and the deep cusp. We define the main body to be the range of the integral where
![]() $|a_{11}|\geq 1$
for some element in
$|a_{11}|\geq 1$
for some element in
![]() $s(Y{\mathcal {B}})$
, and denote the main-body portion of
$s(Y{\mathcal {B}})$
, and denote the main-body portion of
![]() ${\mathcal {I}}_X({\mathcal {L}})$
by
${\mathcal {I}}_X({\mathcal {L}})$
by
![]() ${\mathcal {I}}_X^{\mathrm {{main}}}({\mathcal {L}})$
. We define the shallow cusp to be the range of the integral where
${\mathcal {I}}_X^{\mathrm {{main}}}({\mathcal {L}})$
. We define the shallow cusp to be the range of the integral where
![]() $|a_{11}|< 1$
for all elements in
$|a_{11}|< 1$
for all elements in
![]() $s(Y{\mathcal {B}})$
but
$s(Y{\mathcal {B}})$
but
![]() $|a_{ij}|\geq 1$
for some
$|a_{ij}|\geq 1$
for some
![]() $i,j\leq g$
, and denote the shallow-cusp portion of
$i,j\leq g$
, and denote the shallow-cusp portion of
![]() ${\mathcal {I}}_X({\mathcal {L}})$
by
${\mathcal {I}}_X({\mathcal {L}})$
by
![]() ${\mathcal {I}}_X^{\mathrm {{scusp}}}({\mathcal {L}})$
. We define the deep cusp to be the range of the integral where
${\mathcal {I}}_X^{\mathrm {{scusp}}}({\mathcal {L}})$
. We define the deep cusp to be the range of the integral where
![]() $|a_{ij}|<1$
for all
$|a_{ij}|<1$
for all
![]() $i, j\leq g$
and all elements in
$i, j\leq g$
and all elements in
![]() $s(Y{\mathcal {B}})$
, and denote the deep-cusp portion of
$s(Y{\mathcal {B}})$
, and denote the deep-cusp portion of
![]() ${\mathcal {I}}_X({\mathcal {L}})$
by
${\mathcal {I}}_X({\mathcal {L}})$
by
![]() ${\mathcal {I}}_X^{\mathrm {{dcusp}}}({\mathcal {L}})$
. Then
${\mathcal {I}}_X^{\mathrm {{dcusp}}}({\mathcal {L}})$
. Then
In the next subsection, we prove bounds for the main body, the shallow cusp and the deep cusp when
![]() ${\mathcal {L}}=W({\mathbb {Z}})_{|Q|>M}^{\mathrm {{dist}},\mathrm {{irr}}}$
.
${\mathcal {L}}=W({\mathbb {Z}})_{|Q|>M}^{\mathrm {{dist}},\mathrm {{irr}}}$
.
We will need the following result of Davenport to estimate the number of lattice points in bounded regions.
Proposition 4.1 [Reference Davenport14].
Let
![]() ${\mathcal {R}}$
be a bounded, semi-algebraic multiset in
${\mathcal {R}}$
be a bounded, semi-algebraic multiset in
![]() ${\mathbb {R}}^n$
having maximum multiplicity m that is defined by at most k polynomial inequalities, each having degree at most
${\mathbb {R}}^n$
having maximum multiplicity m that is defined by at most k polynomial inequalities, each having degree at most
![]() $\ell $
. Let
$\ell $
. Let
![]() ${\mathcal {R}}'$
denote the image of
${\mathcal {R}}'$
denote the image of
![]() ${\mathcal {R}}$
under any
${\mathcal {R}}$
under any
![]() $($
upper or lower
$($
upper or lower
![]() $)$
triangular, unipotent transformation of
$)$
triangular, unipotent transformation of
![]() ${\mathbb {R}}^n$
. Then the number of lattice points
${\mathbb {R}}^n$
. Then the number of lattice points
![]() $($
counted with multiplicity
$($
counted with multiplicity
![]() $)$
contained in the region
$)$
contained in the region
![]() ${\mathcal {R}}'$
is given by
${\mathcal {R}}'$
is given by
where
![]() $\overline {\mathrm {{Vol}}}(\overline {{\mathcal {R}}})$
denotes the greatest d-dimensional volume of any projection of
$\overline {\mathrm {{Vol}}}(\overline {{\mathcal {R}}})$
denotes the greatest d-dimensional volume of any projection of
![]() ${\mathcal {R}}$
onto a coordinate subspace obtained by equating
${\mathcal {R}}$
onto a coordinate subspace obtained by equating
![]() $n-d$
coordinates to zero, as d ranges over all values in
$n-d$
coordinates to zero, as d ranges over all values in
![]() $\{1, \dots , n-1\}$
. The implied constant in the second summand depends only on n, m, k and
$\{1, \dots , n-1\}$
. The implied constant in the second summand depends only on n, m, k and
![]() $\ell $
.
$\ell $
.
4.2 The number of orbits of distinguished elements with large Q-invariant
In this subsection, we obtain the following upper bound on
![]() ${\mathcal {I}}_X(W({\mathbb {Z}})^{\mathrm {{dist}},\mathrm {{irr}}}_{|Q|>M})$
, thus yielding the same bound on the quantity
${\mathcal {I}}_X(W({\mathbb {Z}})^{\mathrm {{dist}},\mathrm {{irr}}}_{|Q|>M})$
, thus yielding the same bound on the quantity
![]() $\#\big (\mathrm {{SL}}_n({\mathbb {Z}})\backslash \{w\in W({\mathbb {Z}})^{\mathrm {{dist}},\mathrm {{irr}}}_{|Q|>M}:H(w)<X\}\big )$
by (16).
$\#\big (\mathrm {{SL}}_n({\mathbb {Z}})\backslash \{w\in W({\mathbb {Z}})^{\mathrm {{dist}},\mathrm {{irr}}}_{|Q|>M}:H(w)<X\}\big )$
by (16).
Theorem 4.2. We have
![]() ${\mathcal {I}}_X(W({\mathbb {Z}})^{\mathrm {{dist}},\mathrm {{irr}}}_{|Q|>M}) \ll _\epsilon X^{n+1-1/(2n)+\epsilon } + {X^{n+1+\epsilon }}/{M}.$
${\mathcal {I}}_X(W({\mathbb {Z}})^{\mathrm {{dist}},\mathrm {{irr}}}_{|Q|>M}) \ll _\epsilon X^{n+1-1/(2n)+\epsilon } + {X^{n+1+\epsilon }}/{M}.$
Note that (14), (16), and Theorem 4.2 immediately imply Part (b) of Theorem 5.
We bound
![]() ${\mathcal {I}}_X(W({\mathbb {Z}})^{\mathrm {{dist}},\mathrm {{irr}}}_{|Q|>M})$
by obtaining bounds for the main body, the shallow cusp and the deep cusp. We consider first the main body. In [Reference Ho, Shankar and Varma20, Proposition 4.6], an upper bound of
${\mathcal {I}}_X(W({\mathbb {Z}})^{\mathrm {{dist}},\mathrm {{irr}}}_{|Q|>M})$
by obtaining bounds for the main body, the shallow cusp and the deep cusp. We consider first the main body. In [Reference Ho, Shankar and Varma20, Proposition 4.6], an upper bound of
![]() $o(X^{n+1})$
is obtained on
$o(X^{n+1})$
is obtained on
![]() ${\mathcal {I}}_X^{\mathrm {{main}}}(W({\mathbb {Z}})^{\mathrm {{dist}}})$
. This is proved using the following two ingredients: estimates with a power saving error tern on
${\mathcal {I}}_X^{\mathrm {{main}}}(W({\mathbb {Z}})^{\mathrm {{dist}}})$
. This is proved using the following two ingredients: estimates with a power saving error tern on
![]() ${\mathcal {I}}_X^{\mathrm {{main}}}({\mathcal {L}})$
for lattices
${\mathcal {I}}_X^{\mathrm {{main}}}({\mathcal {L}})$
for lattices
![]() ${\mathcal {L}}\subset W({\mathbb {Z}})$
, and a proof that the density of elements in
${\mathcal {L}}\subset W({\mathbb {Z}})$
, and a proof that the density of elements in
![]() $W({\mathbb {F}}_p)$
that are not
$W({\mathbb {F}}_p)$
that are not
![]() ${\mathbb {F}}_p$
-distinguished is bounded below by some positive constant, independent of p. To obtain a power saving bound on
${\mathbb {F}}_p$
-distinguished is bounded below by some positive constant, independent of p. To obtain a power saving bound on
![]() ${\mathcal {I}}_X(W({\mathbb {Z}})^{\mathrm {{dist}},\mathrm {{irr}}}_{|Q|>M})$
, we use the large sieve.
${\mathcal {I}}_X(W({\mathbb {Z}})^{\mathrm {{dist}},\mathrm {{irr}}}_{|Q|>M})$
, we use the large sieve.
Proposition 4.3. Let
![]() $V\cong {\mathbb {A}}^N$
be an affine space. For every prime p, let
$V\cong {\mathbb {A}}^N$
be an affine space. For every prime p, let
![]() $\Omega _p\subset V({\mathbb {F}}_p)$
and let
$\Omega _p\subset V({\mathbb {F}}_p)$
and let
![]() $\omega (p) = \#\Omega _p/\#V({\mathbb {F}}_p)$
. For a rectangular box
$\omega (p) = \#\Omega _p/\#V({\mathbb {F}}_p)$
. For a rectangular box
![]() ${\mathcal {B}}' = [M_1,M_1+X_1]\times \cdots \times [M_N,M_N+X_N]$
where
${\mathcal {B}}' = [M_1,M_1+X_1]\times \cdots \times [M_N,M_N+X_N]$
where
![]() $M_1,\ldots ,M_N,X_1,\ldots , X_N$
are real numbers with
$M_1,\ldots ,M_N,X_1,\ldots , X_N$
are real numbers with
![]() $X_1,\ldots , X_n$
positive. Let
$X_1,\ldots , X_n$
positive. Let
Then for any
![]() $L> 0$
,
$L> 0$
,
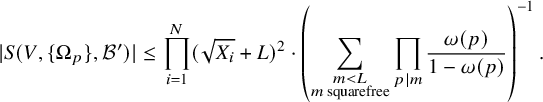 $$ \begin{align} |S(V,\{\Omega_p\},{\mathcal{B}}')| \leq \prod_{i=1}^N (\sqrt{X_i} + L)^2\cdot\left(\sum_{\substack{m < L\\ m\textrm{ }\mathrm{squarefree}}}\prod_{p\mid m}\frac{\omega(p)}{1 - \omega(p)}\right)^{-1}. \end{align} $$
$$ \begin{align} |S(V,\{\Omega_p\},{\mathcal{B}}')| \leq \prod_{i=1}^N (\sqrt{X_i} + L)^2\cdot\left(\sum_{\substack{m < L\\ m\textrm{ }\mathrm{squarefree}}}\prod_{p\mid m}\frac{\omega(p)}{1 - \omega(p)}\right)^{-1}. \end{align} $$
In particular, if
![]() $\omega (p) \gg 1$
, that is, all
$\omega (p) \gg 1$
, that is, all
![]() $\omega (p)$
are bounded below by some positive constant for large enough p, then
$\omega (p)$
are bounded below by some positive constant for large enough p, then
Proof. The bound (18) follows from [Reference Huxley19, Theorem 1] and [Reference Kowalski23, Proposition 2.4]. For the second statement, we have
![]() $\omega (p)/(1 - \omega (p))\gg 1$
, and so
$\omega (p)/(1 - \omega (p))\gg 1$
, and so
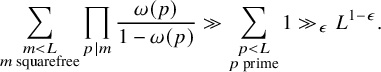 $$ \begin{align*}\sum_{\substack{m < L\\ m\textrm{ }\mathrm{squarefree}}}\prod_{p\mid m}\frac{\omega(p)}{1 - \omega(p)} \gg \sum_{\substack{p < L\\ p\textrm{ }\mathrm{prime}}}1 \gg_\epsilon L^{1 - \epsilon}.\end{align*} $$
$$ \begin{align*}\sum_{\substack{m < L\\ m\textrm{ }\mathrm{squarefree}}}\prod_{p\mid m}\frac{\omega(p)}{1 - \omega(p)} \gg \sum_{\substack{p < L\\ p\textrm{ }\mathrm{prime}}}1 \gg_\epsilon L^{1 - \epsilon}.\end{align*} $$
We are then done by taking
![]() $L = \min \{X_1,\ldots ,X_N\}^{1/2}.$
$L = \min \{X_1,\ldots ,X_N\}^{1/2}.$
In the situation when, for each prime p, a positive density subset of the lattice is being excluded by the sieve, the large sieve yields a better upper bound than the Selberg sieve. See, for example, [Reference Shankar and Tsimerman35], which gives a power-saving error term of
![]() $O_\epsilon (X^{399/400+\epsilon })$
on the count of quintic fields. Applying the large sieve above instead of the Selberg sieve, and following the argument of [Reference Shankar and Tsimerman35], would yield the better error term of
$O_\epsilon (X^{399/400+\epsilon })$
on the count of quintic fields. Applying the large sieve above instead of the Selberg sieve, and following the argument of [Reference Shankar and Tsimerman35], would yield the better error term of
![]() $O_\epsilon (X^{159/160+\epsilon })$
.
$O_\epsilon (X^{159/160+\epsilon })$
.
We now apply the large sieve, as stated in Proposition 4.3, to bound the number of distinguished elements in the main ball:
Proposition 4.4. We have
![]() $ {\mathcal {I}}_X^{\mathrm {{main}}}(W({\mathbb {Z}})^{\mathrm {{dist}}})\ll _\epsilon X^{n+1-1/{(2n)}+\epsilon }. $
$ {\mathcal {I}}_X^{\mathrm {{main}}}(W({\mathbb {Z}})^{\mathrm {{dist}}})\ll _\epsilon X^{n+1-1/{(2n)}+\epsilon }. $
Proof. We apply Proposition 4.3 with
![]() $\Omega _p$
being the set of non-distinguished elements of
$\Omega _p$
being the set of non-distinguished elements of
![]() $w({\mathbb {F}}_p)$
and the rectangular box being
$w({\mathbb {F}}_p)$
and the rectangular box being
![]() $s(Y{\mathcal {B}})$
. The shortest side has length
$s(Y{\mathcal {B}})$
. The shortest side has length
![]() $Yw(a_{11})$
. Note that
$Yw(a_{11})$
. Note that
 $$ \begin{align*}w(a_{11})^{-1/2}\delta(s) = \prod_{k=1}^{n-1}s_k^{n-k}\prod_{k=1}^{n-1}s_k^{-nk(n-k)} = \prod_{k=1}^{n-1}s_k^{(1-nk)(n-k)}\ll 1.\end{align*} $$
$$ \begin{align*}w(a_{11})^{-1/2}\delta(s) = \prod_{k=1}^{n-1}s_k^{n-k}\prod_{k=1}^{n-1}s_k^{-nk(n-k)} = \prod_{k=1}^{n-1}s_k^{(1-nk)(n-k)}\ll 1.\end{align*} $$
Hence, we have
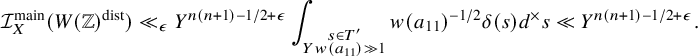 $$ \begin{align*}{\mathcal{I}}_X^{\mathrm{{main}}}(W({\mathbb{Z}})^{\mathrm{{dist}}}) \ll_\epsilon Y^{n(n+1) - 1/2+\epsilon}\int_{\substack{s\in T'\\ Yw(a_{11})\gg 1}}w(a_{11})^{-1/2}\delta(s)d^\times s \ll Y^{n(n+1) - 1/2+\epsilon}.\end{align*} $$
$$ \begin{align*}{\mathcal{I}}_X^{\mathrm{{main}}}(W({\mathbb{Z}})^{\mathrm{{dist}}}) \ll_\epsilon Y^{n(n+1) - 1/2+\epsilon}\int_{\substack{s\in T'\\ Yw(a_{11})\gg 1}}w(a_{11})^{-1/2}\delta(s)d^\times s \ll Y^{n(n+1) - 1/2+\epsilon}.\end{align*} $$
We are now done as
![]() $Y = X^{1/n}$
.
$Y = X^{1/n}$
.
Next, a bound on the shallow cusp follows directly from the proof of [Reference Ho, Shankar and Varma20, Proposition 4.3]:
Proposition 4.5. We have
![]() $ {\mathcal {I}}_X^{\mathrm {{scusp}}}(W({\mathbb {Z}}))\ll X^{n+1-1/{n}}. $
$ {\mathcal {I}}_X^{\mathrm {{scusp}}}(W({\mathbb {Z}}))\ll X^{n+1-1/{n}}. $
In [Reference Ho, Shankar and Varma20, Proposition 4.3], the shallow and deep cusps were treated simultaneously, but the points in the deep cusp were ruled out since only nondistinguished elements were counted there. Hence, the proof of [Reference Ho, Shankar and Varma20, Proposition 4.3] yields the claimed bound in Proposition 4.5.
Finally, to treat the deep cusp, let
![]() $U=\{a_{ij},b_{ij}:1\leq i\leq j\leq n\}$
denote the set of coordinates on W, and let
$U=\{a_{ij},b_{ij}:1\leq i\leq j\leq n\}$
denote the set of coordinates on W, and let
![]() $U_0=\{a_{ij},b_{ij}\mid i\leq j, \:j\geq g+1\}$
denote the set of coordinates on
$U_0=\{a_{ij},b_{ij}\mid i\leq j, \:j\geq g+1\}$
denote the set of coordinates on
![]() $W_0$
. We define a partial order
$W_0$
. We define a partial order
![]() $\lesssim $
on U by setting
$\lesssim $
on U by setting
![]() $\alpha \lesssim \beta $
if all the powers of
$\alpha \lesssim \beta $
if all the powers of
![]() $s_i$
in
$s_i$
in
![]() $w(\alpha )^{-1}w(\beta )$
are nonnegative. Explicitly,
$w(\alpha )^{-1}w(\beta )$
are nonnegative. Explicitly,
![]() $a_{ij}\leq a_{i'j'}$
if and only if
$a_{ij}\leq a_{i'j'}$
if and only if
![]() $i\leq i'$
and
$i\leq i'$
and
![]() $j\leq j'$
(and similarly for
$j\leq j'$
(and similarly for
![]() $b_{ij}$
, as
$b_{ij}$
, as
![]() $a_{ij}$
and
$a_{ij}$
and
![]() $b_{ij}$
have the same weight). A subset
$b_{ij}$
have the same weight). A subset
![]() ${\mathcal {Z}}$
of
${\mathcal {Z}}$
of
![]() $U_0$
is saturated if for any
$U_0$
is saturated if for any
![]() $\beta \in {\mathcal {Z}}$
and any
$\beta \in {\mathcal {Z}}$
and any
![]() $\alpha \in U_0$
with
$\alpha \in U_0$
with
![]() $\alpha \lesssim \beta $
, the coordinate
$\alpha \lesssim \beta $
, the coordinate
![]() $\alpha $
also lies in
$\alpha $
also lies in
![]() ${\mathcal {Z}}$
. We pick positive constants
${\mathcal {Z}}$
. We pick positive constants
![]() $c_{ij}$
for
$c_{ij}$
for
![]() $1\leq i\leq j\leq n$
such that
$1\leq i\leq j\leq n$
such that
-
(a) If
 $|Yw(a_{ij})|<c_{ij}$
, then
$|Yw(a_{ij})|<c_{ij}$
, then
 $|a_{ij}|<1$
and
$|a_{ij}|<1$
and
 $|b_{ij}|<1$
for every
$|b_{ij}|<1$
for every
 $(A,B)\in s(Y{\mathcal {B}})$
.
$(A,B)\in s(Y{\mathcal {B}})$
. -
(b) For all
 $s\in T'$
and
$s\in T'$
and
 $a_{ij}\lesssim a_{i'j'}$
, we have
$a_{ij}\lesssim a_{i'j'}$
, we have
 $w(a_{ij})/c_{ij}\leq w(a_{i'j'})/c_{i'j'}$
.
$w(a_{ij})/c_{ij}\leq w(a_{i'j'})/c_{i'j'}$
.
More explicitly, we may choose
![]() $c_{nn}$
to be sufficiently small and take
$c_{nn}$
to be sufficiently small and take
The significance of these constants
![]() $c_{ij}$
is the following: for every
$c_{ij}$
is the following: for every
![]() $Y>1$
, first, if
$Y>1$
, first, if
![]() $Yw(a_{ij})<c_{ij}$
, then every integral element in
$Yw(a_{ij})<c_{ij}$
, then every integral element in
![]() $s(Y{\mathcal {B}})$
has
$s(Y{\mathcal {B}})$
has
![]() $a_{ij}$
- and
$a_{ij}$
- and
![]() $b_{ij}$
-coordinates equal to
$b_{ij}$
-coordinates equal to
![]() $0$
; and second, if
$0$
; and second, if
![]() $a_{ij}\lesssim a_{i'j'}$
, then
$a_{ij}\lesssim a_{i'j'}$
, then
![]() $Yw(a_{i'j'})<c_{i'j'}$
implies
$Yw(a_{i'j'})<c_{i'j'}$
implies
![]() $Yw(a_{ij})<c_{ij}$
.
$Yw(a_{ij})<c_{ij}$
.
The following lemma gives conditions that ensure an element in
![]() $W({\mathbb {R}})$
has discriminant
$W({\mathbb {R}})$
has discriminant
![]() $0$
.
$0$
.
Lemma 4.6. Suppose that
![]() $(A,B)\in W({\mathbb {R}})$
satisfies
$(A,B)\in W({\mathbb {R}})$
satisfies
![]() $a_{ij}=b_{ij}=0$
for all
$a_{ij}=b_{ij}=0$
for all
![]() $i\leq k$
and
$i\leq k$
and
![]() $j\leq n-k$
for some
$j\leq n-k$
for some
![]() $k\in \{1,\ldots ,g\}$
. Then the discriminant of
$k\in \{1,\ldots ,g\}$
. Then the discriminant of
![]() $(A,B)$
is
$(A,B)$
is
![]() $0$
.
$0$
.
Proof. One checks that
![]() $f_{A,B}$
has a square factor of degree k and so has discriminant
$f_{A,B}$
has a square factor of degree k and so has discriminant
![]() $0$
.
$0$
.
The next lemma states that when
![]() ${\mathcal {L}}\subset W({\mathbb {Z}})$
consists of elements with nonzero discriminant, the integral defining
${\mathcal {L}}\subset W({\mathbb {Z}})$
consists of elements with nonzero discriminant, the integral defining
![]() ${\mathcal {I}}_X({\mathcal {L}})$
can be cut off by conditions of the form
${\mathcal {I}}_X({\mathcal {L}})$
can be cut off by conditions of the form
![]() $s_i\ll X^{\Theta }$
for some absolute constant
$s_i\ll X^{\Theta }$
for some absolute constant
![]() $\Theta $
depending only on n.
$\Theta $
depending only on n.
Lemma 4.7. There exists an absolute constant
![]() $\Theta $
depending only on n such that if
$\Theta $
depending only on n such that if
![]() $s\in T'$
with
$s\in T'$
with
![]() $s_i\gg X^\Theta $
for some i, then
$s_i\gg X^\Theta $
for some i, then
![]() $s(Y{\mathcal {B}})\cap W({\mathbb {Z}})$
contains only points with discriminant
$s(Y{\mathcal {B}})\cap W({\mathbb {Z}})$
contains only points with discriminant
![]() $0$
.
$0$
.
Proof. Let
![]() $s=\mathrm {{diag}}(t_1^{-1},\cdots ,t_n^{-1})\in T'$
; then
$s=\mathrm {{diag}}(t_1^{-1},\cdots ,t_n^{-1})\in T'$
; then
![]() $t_1\gg t_2\gg \cdots \gg t_n$
and
$t_1\gg t_2\gg \cdots \gg t_n$
and
![]() $t_1t_2\cdots t_n=1$
. Because of the relation between the
$t_1t_2\cdots t_n=1$
. Because of the relation between the
![]() $t_j$
’s and the
$t_j$
’s and the
![]() $s_i$
’s, it suffices to prove that if
$s_i$
’s, it suffices to prove that if
![]() $s(Y{\mathcal {B}})$
contains an integral element with nonzero discriminant, then
$s(Y{\mathcal {B}})$
contains an integral element with nonzero discriminant, then
![]() $t_1$
is bounded from above by some power of X or, equivalently,
$t_1$
is bounded from above by some power of X or, equivalently,
![]() $t_n$
is bounded from below by some power of X. By Lemma 4.6, for
$t_n$
is bounded from below by some power of X. By Lemma 4.6, for
![]() $s(Y{\mathcal {B}})$
to contain an integral element with nonzero discriminant, we must have
$s(Y{\mathcal {B}})$
to contain an integral element with nonzero discriminant, we must have
![]() $Yw(a_{k,n-k})\gg 1$
for every
$Yw(a_{k,n-k})\gg 1$
for every
![]() $k\in \{1,\ldots ,g\}$
. That is,
$k\in \{1,\ldots ,g\}$
. That is,
![]() $t_kt_{n-k}\ll Y$
for every
$t_kt_{n-k}\ll Y$
for every
![]() $k\in \{1,\ldots ,g\}$
. Multiplying these conditions together, we obtain
$k\in \{1,\ldots ,g\}$
. Multiplying these conditions together, we obtain
![]() $t_n\gg Y^{-g}$
. The lemma follows.
$t_n\gg Y^{-g}$
. The lemma follows.
We now estimate the contribution to
![]() ${\mathcal {I}}_X(W({\mathbb {Z}})_{|Q|>M}^{\mathrm {{dist}},\mathrm {{irr}}})$
coming from the deep cusp.
${\mathcal {I}}_X(W({\mathbb {Z}})_{|Q|>M}^{\mathrm {{dist}},\mathrm {{irr}}})$
coming from the deep cusp.
Proposition 4.8. We have
![]() $ {\mathcal {I}}_X^{\mathrm {{dcusp}}}(W({\mathbb {Z}})_{|Q|>M}^{\mathrm {{irr}}})\ll _\epsilon {X^{n+1+\epsilon }}/{M}. $
$ {\mathcal {I}}_X^{\mathrm {{dcusp}}}(W({\mathbb {Z}})_{|Q|>M}^{\mathrm {{irr}}})\ll _\epsilon {X^{n+1+\epsilon }}/{M}. $
Proof. For a subset
![]() ${\mathcal {Z}}$
of
${\mathcal {Z}}$
of
![]() $U_0$
, let
$U_0$
, let
![]() $T^{\prime }_{\mathcal {Z}}$
denote the subset of
$T^{\prime }_{\mathcal {Z}}$
denote the subset of
![]() $s\in T'$
with
$s\in T'$
with
![]() $Y^{g(g+1)}w(Q)\gg M$
, and
$Y^{g(g+1)}w(Q)\gg M$
, and
![]() $|Yw(a_{ij})|< c_{ij}$
precisely for those
$|Yw(a_{ij})|< c_{ij}$
precisely for those
![]() $(i,j)$
where
$(i,j)$
where
![]() $a_{ij}\in {\mathcal {Z}}$
or
$a_{ij}\in {\mathcal {Z}}$
or
![]() $b_{ij}\in {\mathcal {Z}}$
. Note that
$b_{ij}\in {\mathcal {Z}}$
. Note that
![]() $T^{\prime }_{\mathcal {Z}}$
is empty if
$T^{\prime }_{\mathcal {Z}}$
is empty if
![]() ${\mathcal {Z}}$
is not saturated. Define
${\mathcal {Z}}$
is not saturated. Define
 $$ \begin{align*} N({\mathcal{Z}},X) &:= \int_{s\in T^{\prime}_{\mathcal{Z}}}\#\big(s(Y{\mathcal{B}})\cap W_0({\mathbb{Z}})\big)\,\delta(s)d^\times s \\ & \ll \int_{s\in T^{\prime}_{\mathcal{Z}}} \Big(\prod_{\alpha\in U_0\backslash {\mathcal{Z}}}Yw(\alpha)\Big) \,\delta(s) d^\times s \\ &= \int_{s\in T^{\prime}_{\mathcal{Z}}} \Big(\prod_{\alpha\in U_0}Yw(\alpha)\Big) \Big(\prod_{\alpha\in {\mathcal{Z}}}Y^{-1}w(\alpha)^{-1}\Big) \,\delta(s) d^\times s, \end{align*} $$
$$ \begin{align*} N({\mathcal{Z}},X) &:= \int_{s\in T^{\prime}_{\mathcal{Z}}}\#\big(s(Y{\mathcal{B}})\cap W_0({\mathbb{Z}})\big)\,\delta(s)d^\times s \\ & \ll \int_{s\in T^{\prime}_{\mathcal{Z}}} \Big(\prod_{\alpha\in U_0\backslash {\mathcal{Z}}}Yw(\alpha)\Big) \,\delta(s) d^\times s \\ &= \int_{s\in T^{\prime}_{\mathcal{Z}}} \Big(\prod_{\alpha\in U_0}Yw(\alpha)\Big) \Big(\prod_{\alpha\in {\mathcal{Z}}}Y^{-1}w(\alpha)^{-1}\Big) \,\delta(s) d^\times s, \end{align*} $$
where the bound on the second line follows from Proposition 4.1. Let
![]() $U' := \{a_{ij},b_{ij}\mid i+j<n\}$
. If
$U' := \{a_{ij},b_{ij}\mid i+j<n\}$
. If
![]() ${\mathcal {Z}}$
is saturated and not contained in
${\mathcal {Z}}$
is saturated and not contained in
![]() $U'$
, then
$U'$
, then
![]() ${\mathcal {Z}}$
contains
${\mathcal {Z}}$
contains
![]() $a_{k,n-k}$
for some
$a_{k,n-k}$
for some
![]() $k=1,\ldots ,g$
. Hence, for any
$k=1,\ldots ,g$
. Hence, for any
![]() $s\in T^{\prime }_{\mathcal {Z}}$
, every integral element in
$s\in T^{\prime }_{\mathcal {Z}}$
, every integral element in
![]() $s(Y {\mathcal {B}})\cap W_0({\mathbb {Z}})$
satisfies
$s(Y {\mathcal {B}})\cap W_0({\mathbb {Z}})$
satisfies
![]() $a_{ij}=b_{ij}=0$
, for
$a_{ij}=b_{ij}=0$
, for
![]() $i\leq k$
and
$i\leq k$
and
![]() $j\leq n-k$
, and so has zero discriminant by Lemma 4.6. Therefore,
$j\leq n-k$
, and so has zero discriminant by Lemma 4.6. Therefore,
where the sum is over saturated subsets
![]() ${\mathcal {Z}}$
of
${\mathcal {Z}}$
of
![]() $U_0$
contained in
$U_0$
contained in
![]() $U'$
.
$U'$
.
Now
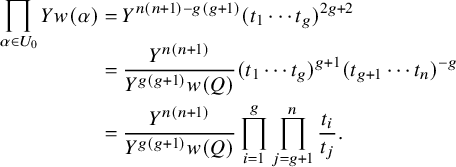 $$ \begin{align} \nonumber\prod_{\alpha\in U_0} Yw(\alpha) &= Y^{n(n+1)-g(g+1)} (t_1\cdots t_{g})^{2g+2}\\[-.1in] \nonumber&= \frac{Y^{n(n+1)}}{Y^{g(g+1)}w(Q)} (t_1\cdots t_{g})^{g+1}(t_{g+1}\cdots t_n)^{-g}\\ &= \frac{Y^{n(n+1)}}{Y^{g(g+1)}w(Q)} \prod_{i=1}^{g}\prod_{j=g+1}^n \frac{t_i}{t_j}. \end{align} $$
$$ \begin{align} \nonumber\prod_{\alpha\in U_0} Yw(\alpha) &= Y^{n(n+1)-g(g+1)} (t_1\cdots t_{g})^{2g+2}\\[-.1in] \nonumber&= \frac{Y^{n(n+1)}}{Y^{g(g+1)}w(Q)} (t_1\cdots t_{g})^{g+1}(t_{g+1}\cdots t_n)^{-g}\\ &= \frac{Y^{n(n+1)}}{Y^{g(g+1)}w(Q)} \prod_{i=1}^{g}\prod_{j=g+1}^n \frac{t_i}{t_j}. \end{align} $$
Fix a saturated subset
![]() ${\mathcal {Z}}$
of
${\mathcal {Z}}$
of
![]() $U_0$
contained in
$U_0$
contained in
![]() $U'$
. We define a map
$U'$
. We define a map
![]() $\pi :{\mathcal {Z}}\rightarrow U_0\backslash U'$
by
$\pi :{\mathcal {Z}}\rightarrow U_0\backslash U'$
by
Note that for any
![]() $\alpha \in {\mathcal {Z}}$
, we have
$\alpha \in {\mathcal {Z}}$
, we have
![]() $\pi (\alpha )\notin U'$
and so
$\pi (\alpha )\notin U'$
and so
![]() $Yw(\pi (\alpha ))\gg 1$
. Furthermore, for every
$Yw(\pi (\alpha ))\gg 1$
. Furthermore, for every
![]() $\alpha \in U'$
, we have
$\alpha \in U'$
, we have
![]() $\alpha \lesssim \pi (\alpha )$
and so
$\alpha \lesssim \pi (\alpha )$
and so
![]() $w(\pi (\alpha ))/w(\alpha )\gg 1$
. Hence, for any
$w(\pi (\alpha ))/w(\alpha )\gg 1$
. Hence, for any
![]() $s\in T^{\prime }_{\mathcal {Z}}$
,
$s\in T^{\prime }_{\mathcal {Z}}$
,
 $$ \begin{align} \prod_{\alpha\in {\mathcal{Z}}} (Yw(\alpha))^{-1} \ll \prod_{\alpha\in {\mathcal{Z}}}\frac{Yw(\pi(\alpha))}{Yw(\alpha)} \ll \prod_{\alpha\in U'}\frac{Yw(\pi(\alpha))}{Yw(\alpha)} = \Big(\prod_{g+1\leq i< j\leq n-1} \frac{t_i}{t_j}\Big) \Big(\prod_{1\leq i< j\leq g+1} \frac{t_i}{t_j}\Big). \end{align} $$
$$ \begin{align} \prod_{\alpha\in {\mathcal{Z}}} (Yw(\alpha))^{-1} \ll \prod_{\alpha\in {\mathcal{Z}}}\frac{Yw(\pi(\alpha))}{Yw(\alpha)} \ll \prod_{\alpha\in U'}\frac{Yw(\pi(\alpha))}{Yw(\alpha)} = \Big(\prod_{g+1\leq i< j\leq n-1} \frac{t_i}{t_j}\Big) \Big(\prod_{1\leq i< j\leq g+1} \frac{t_i}{t_j}\Big). \end{align} $$
Here, the first product on the right-hand side is the contribution from all
![]() $a_{ij}\in U'$
, and the second product is the contribution from all
$a_{ij}\in U'$
, and the second product is the contribution from all
![]() $b_{ij}\in U'$
. Note that when multiplying the right-hand sides of (19) and (20), we get all of the
$b_{ij}\in U'$
. Note that when multiplying the right-hand sides of (19) and (20), we get all of the
![]() $t_i/t_j$
for
$t_i/t_j$
for
![]() $1\leq i < j \leq n$
except for the ones with
$1\leq i < j \leq n$
except for the ones with
![]() $i\geq g+1$
and
$i\geq g+1$
and
![]() $j = n$
. For any
$j = n$
. For any
![]() $s\in T^{\prime }_{\mathcal {Z}}$
, we have
$s\in T^{\prime }_{\mathcal {Z}}$
, we have
![]() $t_i/t_j\gg 1$
for any
$t_i/t_j\gg 1$
for any
![]() $i < j$
, and so
$i < j$
, and so
 $$ \begin{align*}\prod_{\alpha\in U_0\backslash {\mathcal{Z}}}Yw(\alpha) \ll \frac{Y^{n(n+1)}}{Y^{g(g+1)}w(Q)} \prod_{1\leq i < j\leq n} \frac{t_i}{t_j} = \frac{Y^{n(n+1)}}{Y^{g(g+1)}w(Q)}\,\delta(s)^{-1} \ll \frac{Y^{n(n+1)}}{M}\,\delta(s)^{-1}. \end{align*} $$
$$ \begin{align*}\prod_{\alpha\in U_0\backslash {\mathcal{Z}}}Yw(\alpha) \ll \frac{Y^{n(n+1)}}{Y^{g(g+1)}w(Q)} \prod_{1\leq i < j\leq n} \frac{t_i}{t_j} = \frac{Y^{n(n+1)}}{Y^{g(g+1)}w(Q)}\,\delta(s)^{-1} \ll \frac{Y^{n(n+1)}}{M}\,\delta(s)^{-1}. \end{align*} $$
Since each
![]() $s_i$
is bounded below by an absolute constant and bounded above by a power of X by Lemma 4.7, we obtain
$s_i$
is bounded below by an absolute constant and bounded above by a power of X by Lemma 4.7, we obtain
The proof is completed by summing over all saturated subsets
![]() ${\mathcal {Z}}$
contained in
${\mathcal {Z}}$
contained in
![]() $U_1$
.
$U_1$
.
5 A bound on the number of singular symmetric matrices in skewed boxes
Let
![]() $n\geq 2$
be a positive integer and let
$n\geq 2$
be a positive integer and let
![]() $S=\mathrm {{Sym}}_2(n)$
denote the space of symmetric
$S=\mathrm {{Sym}}_2(n)$
denote the space of symmetric
![]() $n\times n$
matrices. Let
$n\times n$
matrices. Let
![]() $|\cdot |$
denote Euclidean length on
$|\cdot |$
denote Euclidean length on
![]() $S({\mathbb {R}})$
obtained by identifying
$S({\mathbb {R}})$
obtained by identifying
![]() $S({\mathbb {R}})$
with
$S({\mathbb {R}})$
with
![]() ${\mathbb {R}}^{\dim S}={\mathbb {R}}^{n(n+1)/2}$
. Let
${\mathbb {R}}^{\dim S}={\mathbb {R}}^{n(n+1)/2}$
. Let
![]() ${\mathcal {D}}\subset S({\mathbb {R}})$
be a bounded open set. For an integer r with
${\mathcal {D}}\subset S({\mathbb {R}})$
be a bounded open set. For an integer r with
![]() $1\leq r<n$
, let
$1\leq r<n$
, let
![]() $S({\mathbb {Z}})_{(r)}$
denote the set of elements in
$S({\mathbb {Z}})_{(r)}$
denote the set of elements in
![]() $S({\mathbb {Z}})$
having rank r. In [Reference Eskin and Katznelson17], Eskin and Katznelson obtained asymptotics for the number of elements in
$S({\mathbb {Z}})$
having rank r. In [Reference Eskin and Katznelson17], Eskin and Katznelson obtained asymptotics for the number of elements in
![]() $Y{\mathcal {D}}\cap S({\mathbb {Z}})_{(r)}$
for
$Y{\mathcal {D}}\cap S({\mathbb {Z}})_{(r)}$
for
![]() $r\in \{1,\ldots ,n-1\}$
.
$r\in \{1,\ldots ,n-1\}$
.
In this paper, we will not need exact asymptotics; upper bounds will suffice. In this section, our goal is to obtain upper bounds on the number of elements of
![]() $S({\mathbb {Z}})_{(r)}$
in skew balls.
$S({\mathbb {Z}})_{(r)}$
in skew balls.
The group
![]() $\mathrm {{SL}}_n$
acts on S via
$\mathrm {{SL}}_n$
acts on S via
![]() $\gamma (A)=\gamma A\gamma ^t$
for
$\gamma (A)=\gamma A\gamma ^t$
for
![]() $\gamma \in \mathrm {{SL}}_n$
and
$\gamma \in \mathrm {{SL}}_n$
and
![]() $A\in S$
. Let
$A\in S$
. Let
![]() $T\subset \mathrm {{SL}}_n({\mathbb {R}})$
denote the subgroup of diagonal matrices with positive coefficients. We denote elements in T by
$T\subset \mathrm {{SL}}_n({\mathbb {R}})$
denote the subgroup of diagonal matrices with positive coefficients. We denote elements in T by
![]() $s=\mathrm {{diag}}(t_1^{-1},\ldots ,t_n^{-1})$
. We are interested in studying the skew ball
$s=\mathrm {{diag}}(t_1^{-1},\ldots ,t_n^{-1})$
. We are interested in studying the skew ball
![]() $s(Y{\mathcal {D}})$
. By symmetry, we may assume that
$s(Y{\mathcal {D}})$
. By symmetry, we may assume that
![]() $s\in T'$
(i.e., we have
$s\in T'$
(i.e., we have
![]() $t_1\gg t_2\gg \ldots \gg t_n$
). Moreover, in light of Lemma 4.7, we will assume that
$t_1\gg t_2\gg \ldots \gg t_n$
). Moreover, in light of Lemma 4.7, we will assume that
![]() $t_1\ll Y^\Theta $
and
$t_1\ll Y^\Theta $
and
![]() $t_n\gg Y^{-\Theta }$
for some absolute constant
$t_n\gg Y^{-\Theta }$
for some absolute constant
![]() $\Theta $
depending only on n.
$\Theta $
depending only on n.
For
![]() $s\in T$
and
$s\in T$
and
![]() $r\in \{1,\ldots ,n-1\}$
, we define the constants
$r\in \{1,\ldots ,n-1\}$
, we define the constants
![]() $C(r,s)$
by
$C(r,s)$
by
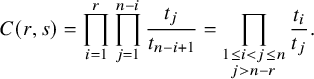 $$ \begin{align} C(r,s) = \prod_{i=1}^r\prod_{j=1}^{n-i}\frac{t_j}{t_{n-i+1}}= \prod_{\substack{1\leq i < j \leq n\\ j> n-r}}\frac{t_i}{t_j}. \end{align} $$
$$ \begin{align} C(r,s) = \prod_{i=1}^r\prod_{j=1}^{n-i}\frac{t_j}{t_{n-i+1}}= \prod_{\substack{1\leq i < j \leq n\\ j> n-r}}\frac{t_i}{t_j}. \end{align} $$
When
![]() $s\in T'$
, these constants satisfy
$s\in T'$
, these constants satisfy
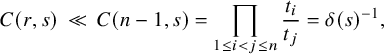 $$ \begin{align*}C(r,s) \,\ll\, C(n-1,s) = \prod_{1 \leq i < j \leq n} \frac{t_i}{t_j} = \delta(s)^{-1},\end{align*} $$
$$ \begin{align*}C(r,s) \,\ll\, C(n-1,s) = \prod_{1 \leq i < j \leq n} \frac{t_i}{t_j} = \delta(s)^{-1},\end{align*} $$
where as before,
![]() $\delta (s)$
is the character of the torus appearing in the Haar measure of
$\delta (s)$
is the character of the torus appearing in the Haar measure of
![]() $\mathrm {{SL}}_n({\mathbb {R}})$
.
$\mathrm {{SL}}_n({\mathbb {R}})$
.
Finally, for
![]() $1\leq r<n$
, a positive real number Y, and
$1\leq r<n$
, a positive real number Y, and
![]() $s\in T$
, let
$s\in T$
, let
![]() $N_r(Y,s)$
denote the number of elements in
$N_r(Y,s)$
denote the number of elements in
![]() $s(Y{\mathcal {D}})\cap S({\mathbb {Z}})_{(r)}$
. We prove the following result.
$s(Y{\mathcal {D}})\cap S({\mathbb {Z}})_{(r)}$
. We prove the following result.
Theorem 5.1. Let
![]() $n\geq 2$
and
$n\geq 2$
and
![]() $1\leq r<n$
be positive integers. Let
$1\leq r<n$
be positive integers. Let
![]() $\Theta>0$
be a real number. Let
$\Theta>0$
be a real number. Let
![]() $Y>1$
be a real number, and let
$Y>1$
be a real number, and let
![]() $s\in T'$
with
$s\in T'$
with
![]() $t_1\ll Y^\Theta $
and
$t_1\ll Y^\Theta $
and
![]() $t_n\gg Y^{-\Theta }$
. Then
$t_n\gg Y^{-\Theta }$
. Then
where the implied constants are independent of s and depend only on n,
![]() ${\mathcal {D}}$
,
${\mathcal {D}}$
,
![]() $\Theta $
and the implied constants in the assumed bounds on
$\Theta $
and the implied constants in the assumed bounds on
![]() $t_1$
and
$t_1$
and
![]() $t_n$
.
$t_n$
.
The case
![]() $s = 1$
of Theorem 5.1 follows from the work of Eskin-Katznelson [Reference Eskin and Katznelson17]. Their strategy is to express the set of singular symmetric matrices of rank r as a union of lattices, each of which consists of elements having a fixed row span. They count the number of elements in each such lattice having bounded norm, and then sum over all possible row spans. We follow this strategy, explaining the modifications necessary to bound integer points in skew balls.
$s = 1$
of Theorem 5.1 follows from the work of Eskin-Katznelson [Reference Eskin and Katznelson17]. Their strategy is to express the set of singular symmetric matrices of rank r as a union of lattices, each of which consists of elements having a fixed row span. They count the number of elements in each such lattice having bounded norm, and then sum over all possible row spans. We follow this strategy, explaining the modifications necessary to bound integer points in skew balls.
Fix positive integers k and m with
![]() $k\leq m$
, and a lattice
$k\leq m$
, and a lattice
![]() $\Lambda $
in
$\Lambda $
in
![]() ${\mathbb {R}}^n$
of rank r. A basis
${\mathbb {R}}^n$
of rank r. A basis
![]() $\{\ell _1,\ldots ,\ell _k\}$
of
$\{\ell _1,\ldots ,\ell _k\}$
of
![]() $\Lambda $
is reduced if the product
$\Lambda $
is reduced if the product
![]() $|\ell _1||\ell _2|\cdots |\ell _k|$
is minimal among all integral bases of
$|\ell _1||\ell _2|\cdots |\ell _k|$
is minimal among all integral bases of
![]() $\Lambda $
. It is almost reduced if
$\Lambda $
. It is almost reduced if
where
![]() $d(\Lambda )$
denotes the covolume of
$d(\Lambda )$
denotes the covolume of
![]() $\Lambda $
in
$\Lambda $
in
![]() $\Lambda \otimes {\mathbb {R}}$
, and the implied constant in the inequality depends only on n. If we order an almost reduced basis
$\Lambda \otimes {\mathbb {R}}$
, and the implied constant in the inequality depends only on n. If we order an almost reduced basis
![]() $\{\ell _1,\ldots ,\ell _k\}$
by length, then the i-th successive minimum of
$\{\ell _1,\ldots ,\ell _k\}$
by length, then the i-th successive minimum of
![]() $\Lambda $
is within a constant multiple (depending only on n) of
$\Lambda $
is within a constant multiple (depending only on n) of
![]() $|\ell _i|$
for every
$|\ell _i|$
for every
![]() $i = 1,\ldots ,k$
. To bound the number elements of
$i = 1,\ldots ,k$
. To bound the number elements of
![]() $\Lambda $
in a ball, we use the following result of Schmidt [Reference Schmidt31].
$\Lambda $
in a ball, we use the following result of Schmidt [Reference Schmidt31].
Proposition 5.2. Let
![]() $\Lambda $
be a rank k lattice in
$\Lambda $
be a rank k lattice in
![]() ${\mathbb {R}}^m$
and
${\mathbb {R}}^m$
and
![]() ${\mathcal {D}}$
a bounded open domain in
${\mathcal {D}}$
a bounded open domain in
![]() ${\mathbb {R}}^m$
. Let
${\mathbb {R}}^m$
. Let
![]() $\mu _1,\ldots ,\mu _k$
be the successive minima of
$\mu _1,\ldots ,\mu _k$
be the successive minima of
![]() $\Lambda $
. Then for
$\Lambda $
. Then for
![]() $Y>0$
, we have
$Y>0$
, we have
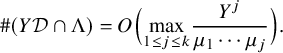 $$ \begin{align} \# (Y{\mathcal{D}}\cap \Lambda) = O\Big(\underset{1\leq j\leq k}{\mathrm{{max}}}\frac{Y^j}{\mu_1\cdots\mu_j}\Big). \end{align} $$
$$ \begin{align} \# (Y{\mathcal{D}}\cap \Lambda) = O\Big(\underset{1\leq j\leq k}{\mathrm{{max}}}\frac{Y^j}{\mu_1\cdots\mu_j}\Big). \end{align} $$
We use the notation of Theorem 5.1. Given a lattice
![]() $\Lambda \subset {\mathbb {Z}}^n$
of rank r, let
$\Lambda \subset {\mathbb {Z}}^n$
of rank r, let
![]() $S(\Lambda )$
denote the set of symmetric matrices
$S(\Lambda )$
denote the set of symmetric matrices
![]() $B\in S({\mathbb {Z}})$
such that the row space (equivalently, the column space) of B is a full rank lattice of
$B\in S({\mathbb {Z}})$
such that the row space (equivalently, the column space) of B is a full rank lattice of
![]() $\Lambda \otimes {\mathbb {R}}$
. Note that
$\Lambda \otimes {\mathbb {R}}$
. Note that
![]() $S(\Lambda )$
will not be a lattice (for example, it does not contain
$S(\Lambda )$
will not be a lattice (for example, it does not contain
![]() $0$
unless
$0$
unless
![]() $r=0$
); we denote the lattice spanned by
$r=0$
); we denote the lattice spanned by
![]() $S(\Lambda )$
in
$S(\Lambda )$
in
![]() $S({\mathbb {Z}})$
by
$S({\mathbb {Z}})$
by
![]() $S'(\Lambda )$
. For two vectors
$S'(\Lambda )$
. For two vectors
![]() $v_1$
and
$v_1$
and
![]() $v_2$
in
$v_2$
in
![]() ${\mathbb {R}}^n$
, we define
${\mathbb {R}}^n$
, we define
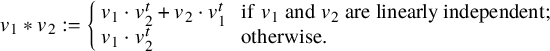 $$ \begin{align} v_1\ast v_2:=\left\{ \begin{array}{ll} v_1\cdot v_2^t+v_2\cdot v_1^t &\;\mathrm{if}\; v_1\;\mathrm{and}\;v_2 \text{ are linearly independent};\\ v_1\cdot v_2^t &\;\mathrm{otherwise}. \end{array}\right. \end{align} $$
$$ \begin{align} v_1\ast v_2:=\left\{ \begin{array}{ll} v_1\cdot v_2^t+v_2\cdot v_1^t &\;\mathrm{if}\; v_1\;\mathrm{and}\;v_2 \text{ are linearly independent};\\ v_1\cdot v_2^t &\;\mathrm{otherwise}. \end{array}\right. \end{align} $$
Then
![]() $v_1\ast v_2=v_2\ast v_1\in S(\text {Span}\{v_1,v_2\})$
, and
$v_1\ast v_2=v_2\ast v_1\in S(\text {Span}\{v_1,v_2\})$
, and
Fix
![]() $\gamma \in \mathrm {{SL}}_n({\mathbb {R}})$
. (For our applications, we will take
$\gamma \in \mathrm {{SL}}_n({\mathbb {R}})$
. (For our applications, we will take
![]() $\gamma \in T$
.) Let
$\gamma \in T$
.) Let
![]() $\Lambda \subseteq {\mathbb {Z}}^n$
be a primitive lattice of rank r. We bound the number of elements in
$\Lambda \subseteq {\mathbb {Z}}^n$
be a primitive lattice of rank r. We bound the number of elements in
![]() $\gamma ^{-1}(Y{\mathcal {D}})\cap S(\Lambda )$
using the bijection
$\gamma ^{-1}(Y{\mathcal {D}})\cap S(\Lambda )$
using the bijection
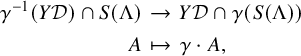 $$ \begin{align*}\begin{array}{rcl}\gamma^{-1}(Y{\mathcal{D}})\cap S(\Lambda)&\to&Y{\mathcal{D}}\cap\gamma(S(\Lambda))\\[.05in]A&\mapsto&\gamma\cdot A,\end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{rcl}\gamma^{-1}(Y{\mathcal{D}})\cap S(\Lambda)&\to&Y{\mathcal{D}}\cap\gamma(S(\Lambda))\\[.05in]A&\mapsto&\gamma\cdot A,\end{array} \end{align*} $$
where
![]() $\gamma \cdot A = \gamma A\gamma ^t$
is the action of
$\gamma \cdot A = \gamma A\gamma ^t$
is the action of
![]() $\gamma $
on A, and instead bounding the number of elements in
$\gamma $
on A, and instead bounding the number of elements in
![]() $Y{\mathcal {D}}\cap \gamma (S(\Lambda ))$
. We thus study the set
$Y{\mathcal {D}}\cap \gamma (S(\Lambda ))$
. We thus study the set
![]() $\gamma (S(\Lambda ))\subset S({\mathbb {R}})$
. The next result, which gives an almost reduced basis for
$\gamma (S(\Lambda ))\subset S({\mathbb {R}})$
. The next result, which gives an almost reduced basis for
![]() $\gamma (S'(\Lambda ))$
in terms of an almost reduced basis of
$\gamma (S'(\Lambda ))$
in terms of an almost reduced basis of
![]() $\gamma \Lambda $
, follows from the proofs of [Reference Eskin and Katznelson17, Proposition 3.3] and [Reference Eskin and Katznelson17, Lemma 3.5].
$\gamma \Lambda $
, follows from the proofs of [Reference Eskin and Katznelson17, Proposition 3.3] and [Reference Eskin and Katznelson17, Lemma 3.5].
Theorem 5.3. Fix
![]() $\gamma \in \mathrm {{SL}}_n({\mathbb {R}})$
. Let
$\gamma \in \mathrm {{SL}}_n({\mathbb {R}})$
. Let
![]() $\Lambda \subset {\mathbb {Z}}^n$
be a primitive lattice of rank r, and let
$\Lambda \subset {\mathbb {Z}}^n$
be a primitive lattice of rank r, and let
![]() $\{\ell _1,\ldots ,\ell _r\}$
be a basis for
$\{\ell _1,\ldots ,\ell _r\}$
be a basis for
![]() $\gamma \Lambda $
. Then
$\gamma \Lambda $
. Then
![]() $\{\ell _i\ast \ell _j\colon 1\leq i\leq j\leq r\}$
is a basis for
$\{\ell _i\ast \ell _j\colon 1\leq i\leq j\leq r\}$
is a basis for
![]() $\gamma (S'(\Lambda ))$
. Furthermore,
$\gamma (S'(\Lambda ))$
. Furthermore,
In particular, if
![]() $\{\ell _1,\ldots ,\ell _r\}$
is almost reduced, then so is
$\{\ell _1,\ldots ,\ell _r\}$
is almost reduced, then so is
![]() $\{\ell _i\ast \ell _j\colon 1\leq i\leq j\leq r\}$
.
$\{\ell _i\ast \ell _j\colon 1\leq i\leq j\leq r\}$
.
Next, by the proof of [Reference Eskin and Katznelson17, Lemma 4.1], we have the following result giving a necessary condition for the set
![]() $Y{\mathcal {D}}\cap \gamma (S(\Lambda ))$
to be nonempty.
$Y{\mathcal {D}}\cap \gamma (S(\Lambda ))$
to be nonempty.
Proposition 5.4. Let
![]() $\gamma \in \mathrm {{SL}}_n({\mathbb {R}})$
and let
$\gamma \in \mathrm {{SL}}_n({\mathbb {R}})$
and let
![]() $\Lambda \subset {\mathbb {Z}}^n$
be a primitive lattice of rank r such that the successive minima of
$\Lambda \subset {\mathbb {Z}}^n$
be a primitive lattice of rank r such that the successive minima of
![]() $\gamma \Lambda $
are
$\gamma \Lambda $
are
![]() $\mu _1\leq \ldots \leq \mu _r$
. If
$\mu _1\leq \ldots \leq \mu _r$
. If
![]() $\#(Y{\mathcal {D}}\cap \gamma (S(\Lambda ))>0$
, then
$\#(Y{\mathcal {D}}\cap \gamma (S(\Lambda ))>0$
, then
![]() $\mu _i\mu _j\leq c_1 Y$
for every pair
$\mu _i\mu _j\leq c_1 Y$
for every pair
![]() $(i,j)$
with
$(i,j)$
with
![]() $i+j\leq r+1$
, for some constant
$i+j\leq r+1$
, for some constant
![]() $c_1$
depending only on n.
$c_1$
depending only on n.
We now prove an upper bound on
![]() $\#(Y{\mathcal {D}}\cap \gamma (S(\Lambda ))$
.
$\#(Y{\mathcal {D}}\cap \gamma (S(\Lambda ))$
.
Proposition 5.5. Let
![]() $\gamma \in \mathrm {{SL}}_n({\mathbb {R}})$
and let
$\gamma \in \mathrm {{SL}}_n({\mathbb {R}})$
and let
![]() $\Lambda \subset {\mathbb {Z}}^n$
be a primitive lattice of rank r such that the successive minima of
$\Lambda \subset {\mathbb {Z}}^n$
be a primitive lattice of rank r such that the successive minima of
![]() $\gamma \Lambda $
are
$\gamma \Lambda $
are
![]() $\mu _1\leq \ldots \leq \mu _r$
. Then
$\mu _1\leq \ldots \leq \mu _r$
. Then
 $$ \begin{align} \#(Y{\mathcal{D}}\cap \gamma(S(\Lambda))= O\Big(\frac{Y^{r(r+1)/2}}{d(\Lambda)^{r+1}} \prod_{\substack{1\leq i< j\leq r\\ i+j\leq r+1}}\frac{\mu_j}{\mu_i}\Big). \end{align} $$
$$ \begin{align} \#(Y{\mathcal{D}}\cap \gamma(S(\Lambda))= O\Big(\frac{Y^{r(r+1)/2}}{d(\Lambda)^{r+1}} \prod_{\substack{1\leq i< j\leq r\\ i+j\leq r+1}}\frac{\mu_j}{\mu_i}\Big). \end{align} $$
Proof. Let
![]() $U(r)$
denote the set of pairs
$U(r)$
denote the set of pairs
![]() $(i,j)$
of positive integers such that
$(i,j)$
of positive integers such that
![]() $i\leq j\leq r$
and
$i\leq j\leq r$
and
![]() $i+j>r+1$
. In other words, elements in
$i+j>r+1$
. In other words, elements in
![]() $U(r)$
correspond to the successive minima of the lattice
$U(r)$
correspond to the successive minima of the lattice
![]() $\gamma (S'(\Lambda ))$
that are
$\gamma (S'(\Lambda ))$
that are
![]() $\gg Y$
. By Proposition 5.2, Theorem 5.3 and (24), we have
$\gg Y$
. By Proposition 5.2, Theorem 5.3 and (24), we have
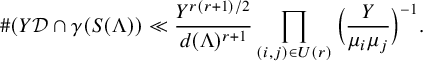 $$ \begin{align*} \#(Y{\mathcal{D}}\cap \gamma(S(\Lambda))\ll \frac{Y^{r(r+1)/2}}{d(\Lambda)^{r+1}} \prod_{(i,j)\in U(r)}\Big(\frac{Y}{\mu_i\mu_j}\Big)^{-1}. \end{align*} $$
$$ \begin{align*} \#(Y{\mathcal{D}}\cap \gamma(S(\Lambda))\ll \frac{Y^{r(r+1)/2}}{d(\Lambda)^{r+1}} \prod_{(i,j)\in U(r)}\Big(\frac{Y}{\mu_i\mu_j}\Big)^{-1}. \end{align*} $$
Assume that
![]() $\#(Y{\mathcal {D}}\cap \gamma (S(\Lambda ))>0$
. Then
$\#(Y{\mathcal {D}}\cap \gamma (S(\Lambda ))>0$
. Then
![]() $\mu _{r+1-j}\mu _j\ll Y$
for all
$\mu _{r+1-j}\mu _j\ll Y$
for all
![]() $1\leq j\leq r$
by Proposition 5.4. Thus,
$1\leq j\leq r$
by Proposition 5.4. Thus,
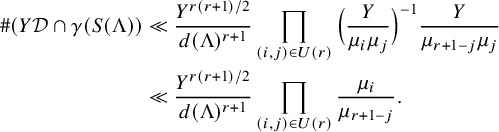 $$ \begin{align} \#(Y{\mathcal{D}}\cap \gamma(S(\Lambda)) &\ll \frac{Y^{r(r+1)/2}}{d(\Lambda)^{r+1}}\prod_{(i,j)\in U(r)} \Big(\frac{Y}{\mu_i\mu_j}\Big)^{-1}\frac{Y}{\mu_{r+1-j}\mu_j} \nonumber\\ &\ll \frac{Y^{r(r+1)/2}}{d(\Lambda)^{r+1}}\prod_{(i,j)\in U(r)} \frac{\mu_i}{\mu_{r+1-j}}. \end{align} $$
$$ \begin{align} \#(Y{\mathcal{D}}\cap \gamma(S(\Lambda)) &\ll \frac{Y^{r(r+1)/2}}{d(\Lambda)^{r+1}}\prod_{(i,j)\in U(r)} \Big(\frac{Y}{\mu_i\mu_j}\Big)^{-1}\frac{Y}{\mu_{r+1-j}\mu_j} \nonumber\\ &\ll \frac{Y^{r(r+1)/2}}{d(\Lambda)^{r+1}}\prod_{(i,j)\in U(r)} \frac{\mu_i}{\mu_{r+1-j}}. \end{align} $$
Since
![]() $i\leq j$
and
$i\leq j$
and
![]() $i+j>r+1$
for
$i+j>r+1$
for
![]() $(i,j)\in U(r)$
, we have the following injection:
$(i,j)\in U(r)$
, we have the following injection:
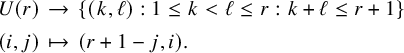 $$ \begin{align} \begin{array}{rcl} U(r)&\to& \{(k,\ell):1\leq k< \ell\leq r:k+\ell\leq r+1\} \\[.05in] (i,j)&\mapsto& (r+1-j,i). \end{array} \end{align} $$
$$ \begin{align} \begin{array}{rcl} U(r)&\to& \{(k,\ell):1\leq k< \ell\leq r:k+\ell\leq r+1\} \\[.05in] (i,j)&\mapsto& (r+1-j,i). \end{array} \end{align} $$
Since
![]() $\frac {\mu _j}{\mu _i}\geq 1$
for
$\frac {\mu _j}{\mu _i}\geq 1$
for
![]() $j>i$
, the injection (27) implies that the product of the ratios
$j>i$
, the injection (27) implies that the product of the ratios
![]() $\mu _j/\mu _i$
in (25) is at least as large as the product of the ratios
$\mu _j/\mu _i$
in (25) is at least as large as the product of the ratios
![]() $\mu _i/\mu _{r+1-j}$
in (26). The result follows.
$\mu _i/\mu _{r+1-j}$
in (26). The result follows.
We now sum over the appropriate lattices
![]() $\Lambda \subset {\mathbb {Z}}^n$
having rank r. To this end, we fix an element
$\Lambda \subset {\mathbb {Z}}^n$
having rank r. To this end, we fix an element
![]() $s=\mathrm {{diag}}(t_1^{-1},t_2^{-1},\dots ,t_n^{-1})\in T'$
. We will apply the previous results with
$s=\mathrm {{diag}}(t_1^{-1},t_2^{-1},\dots ,t_n^{-1})\in T'$
. We will apply the previous results with
![]() $\gamma =s^{-1}$
. Set
$\gamma =s^{-1}$
. Set
![]() $L=(L_1,\ldots ,L_r)$
with
$L=(L_1,\ldots ,L_r)$
with
![]() $0<L_1\leq L_2\leq \cdots \leq L_r$
. Let
$0<L_1\leq L_2\leq \cdots \leq L_r$
. Let
![]() $\Sigma (L,s)$
denote the set of primitive lattices
$\Sigma (L,s)$
denote the set of primitive lattices
![]() $\Lambda \subset {\mathbb {Z}}^n$
of rank r whose successive minima
$\Lambda \subset {\mathbb {Z}}^n$
of rank r whose successive minima
![]() $\mu _1,\ldots ,\mu _r$
of
$\mu _1,\ldots ,\mu _r$
of
![]() $s^{-1}\Lambda $
satisfy
$s^{-1}\Lambda $
satisfy
![]() $L_i\leq \mu _i<2L_i$
for each i.
$L_i\leq \mu _i<2L_i$
for each i.
Lemma 5.6. Let
![]() $L=(L_1,\ldots ,L_r)$
and
$L=(L_1,\ldots ,L_r)$
and
![]() $s=\mathrm {{diag}}(t_1^{-1},\ldots ,t_n^{-1})\in T'$
. Then there is a constant
$s=\mathrm {{diag}}(t_1^{-1},\ldots ,t_n^{-1})\in T'$
. Then there is a constant
![]() $c'>0$
depending only on n such that if
$c'>0$
depending only on n such that if
![]() $\#\Sigma (L,s)> 0$
, then
$\#\Sigma (L,s)> 0$
, then
![]() $L_it_j^{-1}> c'$
for all
$L_it_j^{-1}> c'$
for all
![]() $(i,j)$
with
$(i,j)$
with
![]() $i+j\geq n+1$
.
$i+j\geq n+1$
.
Proof. Since
![]() $\#\Sigma (L,s)> 0$
, there exists an integral lattice
$\#\Sigma (L,s)> 0$
, there exists an integral lattice
![]() $\Lambda \subset {\mathbb {Z}}^n$
of rank r with basis
$\Lambda \subset {\mathbb {Z}}^n$
of rank r with basis
![]() $\{\ell _1,\ldots ,\ell _r\}$
such that
$\{\ell _1,\ldots ,\ell _r\}$
such that
![]() $|s^{-1}\ell _i|<2L_i$
for
$|s^{-1}\ell _i|<2L_i$
for
![]() $i\in \{1,\ldots ,r\}$
. For
$i\in \{1,\ldots ,r\}$
. For
![]() $1\leq j\leq n$
, let
$1\leq j\leq n$
, let
![]() $u_{ij}$
denote the (integral) j-th entry of
$u_{ij}$
denote the (integral) j-th entry of
![]() $\ell _i$
. Then
$\ell _i$
. Then
![]() $|u_{ij}|\leq 2L_it_j^{-1}$
for every
$|u_{ij}|\leq 2L_it_j^{-1}$
for every
![]() $1\leq i\leq r$
and
$1\leq i\leq r$
and
![]() $1\leq j\leq n$
. The assumption that
$1\leq j\leq n$
. The assumption that
![]() $s\in T'$
implies that
$s\in T'$
implies that
![]() $L_it_j^{-1}\ll L_{i'}t_{j'}^{-1}$
whenever
$L_it_j^{-1}\ll L_{i'}t_{j'}^{-1}$
whenever
![]() $i\leq i'$
and
$i\leq i'$
and
![]() $j\leq j'$
.
$j\leq j'$
.
Suppose that there is an integer k with
![]() $1\leq k\leq r$
such that
$1\leq k\leq r$
such that
![]() $L_kt_{n+1-k}^{-1}<c"$
for some sufficiently small constant
$L_kt_{n+1-k}^{-1}<c"$
for some sufficiently small constant
![]() $c">0$
. Then
$c">0$
. Then
![]() $|u_{ij}|<1$
, and thus,
$|u_{ij}|<1$
, and thus,
![]() $u_{ij}=0$
for all
$u_{ij}=0$
for all
![]() $(i,j)$
with
$(i,j)$
with
![]() $1\leq i\leq k$
and
$1\leq i\leq k$
and
![]() $1\leq j\leq n+1-k$
. However, this implies that the vectors
$1\leq j\leq n+1-k$
. However, this implies that the vectors
![]() $\ell _1,\ldots ,\ell _k$
are not linearly independent, a contradiction. Hence, such a k does not exist and
$\ell _1,\ldots ,\ell _k$
are not linearly independent, a contradiction. Hence, such a k does not exist and
![]() $L_kt_{n+1-k}^{-1}\gg 1$
for all k, implying the result.
$L_kt_{n+1-k}^{-1}\gg 1$
for all k, implying the result.
We now determine an upper bound for
![]() $\#\Sigma (L,s)$
.
$\#\Sigma (L,s)$
.
Proposition 5.7. Let
![]() $L=(L_1,\ldots ,L_r)$
and
$L=(L_1,\ldots ,L_r)$
and
![]() $s=\mathrm {{diag}}(t_1^{-1},\ldots ,t_n^{-1})\in T'$
. Then
$s=\mathrm {{diag}}(t_1^{-1},\ldots ,t_n^{-1})\in T'$
. Then
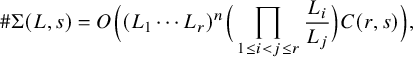 $$ \begin{align} \#\Sigma(L,s) = O\Big((L_1\cdots L_r)^n \Big(\prod_{1\leq i < j\leq r}\frac{L_i}{L_j}\Big) C(r,s)\Big), \end{align} $$
$$ \begin{align} \#\Sigma(L,s) = O\Big((L_1\cdots L_r)^n \Big(\prod_{1\leq i < j\leq r}\frac{L_i}{L_j}\Big) C(r,s)\Big), \end{align} $$
where
![]() $C(r,s)$
is defined as in (21).
$C(r,s)$
is defined as in (21).
Proof. We count lattices
![]() $\Lambda $
by counting r-tuples of vectors
$\Lambda $
by counting r-tuples of vectors
![]() $(\ell _1,\ldots ,\ell _r)$
such that each
$(\ell _1,\ldots ,\ell _r)$
such that each
![]() $\ell _i\in s^{-1}{\mathbb {Z}}^n$
satisfies
$\ell _i\in s^{-1}{\mathbb {Z}}^n$
satisfies
![]() $L_i\leq |\ell _i| < 2L_i$
and such that
$L_i\leq |\ell _i| < 2L_i$
and such that
![]() $\{\ell _1,\ldots ,\ell _r\}$
is a reduced basis of the lattice it generates. For each
$\{\ell _1,\ldots ,\ell _r\}$
is a reduced basis of the lattice it generates. For each
![]() $i = 1,\ldots ,r$
, let
$i = 1,\ldots ,r$
, let
![]() $\alpha (i)$
be the largest integer such that
$\alpha (i)$
be the largest integer such that
![]() $L_it_{\alpha (i)}^{-1}\leq c'$
, where
$L_it_{\alpha (i)}^{-1}\leq c'$
, where
![]() $c'$
is as in Lemma 5.6, or let
$c'$
is as in Lemma 5.6, or let
![]() $\alpha (i)=0$
if no such integer exists. By Proposition 5.2, the number of possibilities for
$\alpha (i)=0$
if no such integer exists. By Proposition 5.2, the number of possibilities for
![]() $\ell _i$
is
$\ell _i$
is
 $$ \begin{align*} \ll\; \prod_{j=1}^n \mathrm{{max}}\big(L_it_j^{-1},1\big)\;\ll\; L_i^n\prod_{j=1}^{\alpha(i)}\big(L_i^{-1}t_j\big). \end{align*} $$
$$ \begin{align*} \ll\; \prod_{j=1}^n \mathrm{{max}}\big(L_it_j^{-1},1\big)\;\ll\; L_i^n\prod_{j=1}^{\alpha(i)}\big(L_i^{-1}t_j\big). \end{align*} $$
However, once
![]() $\ell _1$
is fixed, and given a vector
$\ell _1$
is fixed, and given a vector
![]() $\ell _2$
, at most two of
$\ell _2$
, at most two of
![]() $\ell _2-k\ell _1$
can be part of a reduced basis for
$\ell _2-k\ell _1$
can be part of a reduced basis for
![]() $k\in {\mathbb {Z}}$
. Since
$k\in {\mathbb {Z}}$
. Since
![]() $\gg L_2/L_1$
vectors
$\gg L_2/L_1$
vectors
![]() $\ell _2-k\ell _1$
satisfy the same size bound as
$\ell _2-k\ell _1$
satisfy the same size bound as
![]() $\ell _2$
(namely, those with
$\ell _2$
(namely, those with
![]() $k\ll L_2/L_1$
), the number of choices for the pair
$k\ll L_2/L_1$
), the number of choices for the pair
![]() $(\ell _1,\ell _2)$
that are part of a reduced basis is
$(\ell _1,\ell _2)$
that are part of a reduced basis is
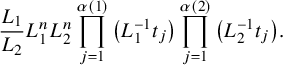 $$ \begin{align*} \frac{L_1}{L_2}L_1^nL_2^n \prod_{j=1}^{\alpha(1)}\big(L_1^{-1}t_j\big) \prod_{j=1}^{\alpha(2)}\big(L_2^{-1}t_j\big). \end{align*} $$
$$ \begin{align*} \frac{L_1}{L_2}L_1^nL_2^n \prod_{j=1}^{\alpha(1)}\big(L_1^{-1}t_j\big) \prod_{j=1}^{\alpha(2)}\big(L_2^{-1}t_j\big). \end{align*} $$
Continuing in this way, we obtain the bound
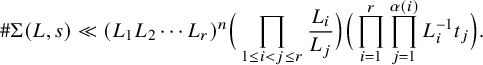 $$ \begin{align} \#\Sigma(L,s)\ll (L_1L_2\cdots L_r)^n \Big(\prod_{1\leq i < j\leq r}\frac{L_i}{L_j}\Big) \Big(\prod_{i=1}^r\prod_{j=1}^{\alpha(i)}L_i^{-1}t_j\Big). \end{align} $$
$$ \begin{align} \#\Sigma(L,s)\ll (L_1L_2\cdots L_r)^n \Big(\prod_{1\leq i < j\leq r}\frac{L_i}{L_j}\Big) \Big(\prod_{i=1}^r\prod_{j=1}^{\alpha(i)}L_i^{-1}t_j\Big). \end{align} $$
By Lemma 5.6, we have
![]() $\alpha (i)\leq n-i$
for
$\alpha (i)\leq n-i$
for
![]() $i\in \{1,\ldots ,r\}$
. Therefore,
$i\in \{1,\ldots ,r\}$
. Therefore,
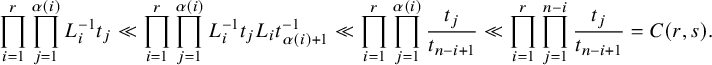 $$ \begin{align} \prod_{i=1}^r\prod_{j=1}^{\alpha(i)}L_i^{-1}t_j \ll \prod_{i=1}^r\prod_{j=1}^{\alpha(i)}L_i^{-1}t_j L_it_{\alpha(i)+1}^{-1} \ll \prod_{i=1}^r\prod_{j=1}^{\alpha(i)}\frac{t_j}{t_{n-i+1}} \ll \prod_{i=1}^r\prod_{j=1}^{n-i}\frac{t_j}{t_{n-i+1}} = C(r,s). \end{align} $$
$$ \begin{align} \prod_{i=1}^r\prod_{j=1}^{\alpha(i)}L_i^{-1}t_j \ll \prod_{i=1}^r\prod_{j=1}^{\alpha(i)}L_i^{-1}t_j L_it_{\alpha(i)+1}^{-1} \ll \prod_{i=1}^r\prod_{j=1}^{\alpha(i)}\frac{t_j}{t_{n-i+1}} \ll \prod_{i=1}^r\prod_{j=1}^{n-i}\frac{t_j}{t_{n-i+1}} = C(r,s). \end{align} $$
We are now ready to prove the main result of this section.
Proof of Theorem 5.1.
Let
![]() $L=(L_1,\ldots ,L_r)$
be a tuple such that
$L=(L_1,\ldots ,L_r)$
be a tuple such that
![]() $0<L_1\leq L_2\leq \cdots \leq L_r$
. Then, by Lemma 5.6, Proposition 5.4 and the definition of
$0<L_1\leq L_2\leq \cdots \leq L_r$
. Then, by Lemma 5.6, Proposition 5.4 and the definition of
![]() $T'$
, we see that for there to exist a lattice
$T'$
, we see that for there to exist a lattice
![]() $\Lambda \in \Sigma (L,s)$
such that
$\Lambda \in \Sigma (L,s)$
such that
![]() $\#(Y{\mathcal {D}}\cap s^{-1}(S(\Lambda ))>0$
, we must have
$\#(Y{\mathcal {D}}\cap s^{-1}(S(\Lambda ))>0$
, we must have
for some absolute constants
![]() $\Theta _1,\Theta _2>0$
. For any such
$\Theta _1,\Theta _2>0$
. For any such
![]() $\Lambda $
, Proposition 5.5 states that
$\Lambda $
, Proposition 5.5 states that
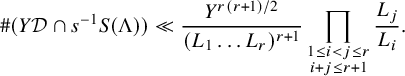 $$ \begin{align*} \#(Y{\mathcal{D}}\cap s^{-1}S(\Lambda))\ll \frac{Y^{r(r+1)/2}}{(L_1\ldots L_r)^{r+1}} \prod_{\substack{1\leq i<j\leq r\\i+j\leq r+1}}\frac{L_j}{L_i}. \end{align*} $$
$$ \begin{align*} \#(Y{\mathcal{D}}\cap s^{-1}S(\Lambda))\ll \frac{Y^{r(r+1)/2}}{(L_1\ldots L_r)^{r+1}} \prod_{\substack{1\leq i<j\leq r\\i+j\leq r+1}}\frac{L_j}{L_i}. \end{align*} $$
Thus,
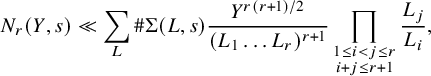 $$ \begin{align*} N_r(Y,s)\ll \sum_L \#\Sigma(L,s) \frac{Y^{r(r+1)/2}}{(L_1\ldots L_r)^{r+1}} \prod_{\substack{1\leq i<j\leq r\\i+j\leq r+1}}\frac{L_j}{L_i}, \end{align*} $$
$$ \begin{align*} N_r(Y,s)\ll \sum_L \#\Sigma(L,s) \frac{Y^{r(r+1)/2}}{(L_1\ldots L_r)^{r+1}} \prod_{\substack{1\leq i<j\leq r\\i+j\leq r+1}}\frac{L_j}{L_i}, \end{align*} $$
where the sum is over r-tuples
![]() $L=(L_1,\ldots ,L_r)$
with
$L=(L_1,\ldots ,L_r)$
with
![]() $L_1\leq L_2\leq \cdots \leq L_n$
that partition the region
$L_1\leq L_2\leq \cdots \leq L_n$
that partition the region
![]() $\{(\mu _1,\ldots ,\mu _r)\in [Y^{-\Theta },Y^{\Theta '}]^r:\mu _1\leq \ldots \leq \mu _r\}$
into dyadic ranges. The sum over L has length
$\{(\mu _1,\ldots ,\mu _r)\in [Y^{-\Theta },Y^{\Theta '}]^r:\mu _1\leq \ldots \leq \mu _r\}$
into dyadic ranges. The sum over L has length
![]() $O(\log ^r Y)$
. Using the upper bound on
$O(\log ^r Y)$
. Using the upper bound on
![]() $\#\Sigma (L,s)$
in Proposition 5.7, we obtain
$\#\Sigma (L,s)$
in Proposition 5.7, we obtain
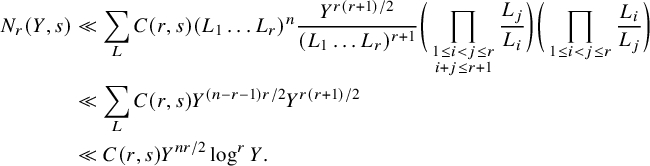 $$ \begin{align*} N_r(Y,s) &\ll \sum_L C(r,s)(L_1\ldots L_r)^{n}\frac{Y^{r(r+1)/2}}{(L_1\ldots L_r)^{r+1}} \bigg(\prod_{\substack{1\leq i<j\leq r\\i+j\leq r+1}}\frac{L_j}{L_i}\bigg) \bigg(\prod_{1\leq i < j\leq r}\frac{L_i}{L_j}\bigg) \\ &\ll \sum_LC(r,s)Y^{(n-r-1)r/2}Y^{r(r+1)/2} \\ &\ll C(r,s)Y^{nr/2}\log^r Y. \end{align*} $$
$$ \begin{align*} N_r(Y,s) &\ll \sum_L C(r,s)(L_1\ldots L_r)^{n}\frac{Y^{r(r+1)/2}}{(L_1\ldots L_r)^{r+1}} \bigg(\prod_{\substack{1\leq i<j\leq r\\i+j\leq r+1}}\frac{L_j}{L_i}\bigg) \bigg(\prod_{1\leq i < j\leq r}\frac{L_i}{L_j}\bigg) \\ &\ll \sum_LC(r,s)Y^{(n-r-1)r/2}Y^{r(r+1)/2} \\ &\ll C(r,s)Y^{nr/2}\log^r Y. \end{align*} $$
This concludes the proof of Theorem 5.1.
6 A uniformity estimate for even degree polynomials
We fix an even integer
![]() $n=2g+2$
with
$n=2g+2$
with
![]() $g\geq 1$
. Our goal is to prove Theorem 5(c) by obtaining a bound on the number of integral binary n-ic forms having bounded height having discriminant weakly divisible by the square of a large squarefree integer.
$g\geq 1$
. Our goal is to prove Theorem 5(c) by obtaining a bound on the number of integral binary n-ic forms having bounded height having discriminant weakly divisible by the square of a large squarefree integer.
Throughout this section, we write
![]() $V:=V_n$
and
$V:=V_n$
and
![]() $W:=W_{n+1}$
. Let
$W:=W_{n+1}$
. Let
![]() $m>0$
be an odd squarefree integer, and let
$m>0$
be an odd squarefree integer, and let
![]() ${\mathcal {W}}_m^{\mathrm {{{(2)}}}}:={\mathcal {W}}_{m,n}^{\mathrm {{{(2)}}}}$
. We also define the following auxiliary sets:
${\mathcal {W}}_m^{\mathrm {{{(2)}}}}:={\mathcal {W}}_{m,n}^{\mathrm {{{(2)}}}}$
. We also define the following auxiliary sets:
where
![]() $\kappa>0$
is a small constant (whose exact value will be optimized later) and
$\kappa>0$
is a small constant (whose exact value will be optimized later) and
![]() $\mathrm {{Gal}}$
denotes the Galois group. Then, for any
$\mathrm {{Gal}}$
denotes the Galois group. Then, for any
![]() $M>0$
, we have the following containment:
$M>0$
, we have the following containment:
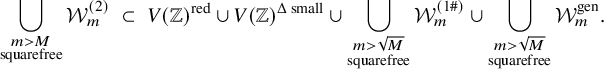 $$ \begin{align} \bigcup_{\substack{m>M\\\mathrm{squarefree}}} {\mathcal{W}}_{m}^{(2)}\;\subset\; V({\mathbb{Z}})^{\mathrm{{red}}}\cup V({\mathbb{Z}})^{\Delta\text{\,small}} \cup\bigcup_{\substack{m>\sqrt{M}\\\mathrm{squarefree}}} {\mathcal{W}}_{m}^{(1\#)}\cup\bigcup_{\substack{m>\sqrt{M}\\\mathrm{squarefree}}} {\mathcal{W}}_{m}^{\mathrm{{gen}}}. \end{align} $$
$$ \begin{align} \bigcup_{\substack{m>M\\\mathrm{squarefree}}} {\mathcal{W}}_{m}^{(2)}\;\subset\; V({\mathbb{Z}})^{\mathrm{{red}}}\cup V({\mathbb{Z}})^{\Delta\text{\,small}} \cup\bigcup_{\substack{m>\sqrt{M}\\\mathrm{squarefree}}} {\mathcal{W}}_{m}^{(1\#)}\cup\bigcup_{\substack{m>\sqrt{M}\\\mathrm{squarefree}}} {\mathcal{W}}_{m}^{\mathrm{{gen}}}. \end{align} $$
The number of elements in
![]() $V({\mathbb {Z}})^{\mathrm {{red}}}$
having height less than X was bounded by
$V({\mathbb {Z}})^{\mathrm {{red}}}$
having height less than X was bounded by
![]() $O(X^n$
) in [Reference Kuba22, Theorem 1]. We next prove a bound on the number of elements in
$O(X^n$
) in [Reference Kuba22, Theorem 1]. We next prove a bound on the number of elements in
![]() $V({\mathbb {Z}})^{\Delta \text {\,small}}$
of bounded height.
$V({\mathbb {Z}})^{\Delta \text {\,small}}$
of bounded height.
Lemma 6.1. The number of integral binary n-ic forms with height less than X and absolute discriminant less than
![]() $X^{2n-2-\kappa }$
is
$X^{2n-2-\kappa }$
is
![]() $O(X^{n+1 - \frac {\kappa }{2n-2}})$
.
$O(X^{n+1 - \frac {\kappa }{2n-2}})$
.
Proof. Set
![]() $\eta := \kappa /(2n-2)$
. The number of integral binary n-ic forms
$\eta := \kappa /(2n-2)$
. The number of integral binary n-ic forms
![]() $a_0x^n + \cdots + a_ny^n$
with height less than X such that
$a_0x^n + \cdots + a_ny^n$
with height less than X such that
![]() $|a_0|\leq X^{1-\eta }$
is
$|a_0|\leq X^{1-\eta }$
is
![]() $O(X^{n+1-\eta })$
. Hence, we assume
$O(X^{n+1-\eta })$
. Hence, we assume
![]() $|a_0|>X^{1-\eta }.$
$|a_0|>X^{1-\eta }.$
Now fix integers
![]() $a_0,\ldots ,a_{n-1}$
with
$a_0,\ldots ,a_{n-1}$
with
![]() $|a_i|\leq X$
and
$|a_i|\leq X$
and
![]() $|a_0|>X^{1-\eta }$
. The discriminant of
$|a_0|>X^{1-\eta }$
. The discriminant of
![]() $a_0x^n + \cdots + a_ny^n$
is a polynomial
$a_0x^n + \cdots + a_ny^n$
is a polynomial
![]() $F(a_n)$
in
$F(a_n)$
in
![]() $a_n$
of degree
$a_n$
of degree
![]() $n-1$
with leading coefficient
$n-1$
with leading coefficient
![]() $C_na_0^{n-1}$
for some nonzero constant
$C_na_0^{n-1}$
for some nonzero constant
![]() $C_n$
. Let
$C_n$
. Let
![]() $r_1,\ldots ,r_{n-1}\in {\mathbb {C}}$
be the
$r_1,\ldots ,r_{n-1}\in {\mathbb {C}}$
be the
![]() $n-1$
roots of
$n-1$
roots of
![]() $F(x)$
. Then
$F(x)$
. Then
Since
![]() $|F(a_n)| < X^{2n-2-\kappa }$
, we have
$|F(a_n)| < X^{2n-2-\kappa }$
, we have
![]() $(a_n-r_1)\cdots (a_n-r_{n-1})\ll X^{n-1-(n-1)\eta }$
. Hence,
$(a_n-r_1)\cdots (a_n-r_{n-1})\ll X^{n-1-(n-1)\eta }$
. Hence,
![]() $|a_n - r_i| \ll X^{1-\eta }$
for some
$|a_n - r_i| \ll X^{1-\eta }$
for some
![]() $i=1,\ldots ,n-1$
. The number of such integers
$i=1,\ldots ,n-1$
. The number of such integers
![]() $a_n$
is
$a_n$
is
![]() $O(X^{1-\eta })$
. Since there are
$O(X^{1-\eta })$
. Since there are
![]() $O(X^n)$
choices for
$O(X^n)$
choices for
![]() $a_0,\ldots ,a_{n-1}$
, we obtain the desired bound.
$a_0,\ldots ,a_{n-1}$
, we obtain the desired bound.
A direct application of a quantitative version of the Ekedahl sieve as in [Reference Bhargava4, Theorem 3.3] implies the following bound on the number of elements of bounded height belonging to
![]() ${\mathcal {W}}^{(1\#)}_{m}$
for large m.
${\mathcal {W}}^{(1\#)}_{m}$
for large m.
Lemma 6.2. We have
 $ \#\!\!\bigcup _{\substack {m>\sqrt {M}\\ m\;\mathrm {squarefree}}} \!\!\{f\in {\mathcal {W}}_{m}^{(1\#)}:H(f)<X\} = O\Big (\frac {X^{n+1}}{\sqrt {M}} + X^n\Big ). $
$ \#\!\!\bigcup _{\substack {m>\sqrt {M}\\ m\;\mathrm {squarefree}}} \!\!\{f\in {\mathcal {W}}_{m}^{(1\#)}:H(f)<X\} = O\Big (\frac {X^{n+1}}{\sqrt {M}} + X^n\Big ). $
To prove Theorem 5(c), it thus remains to obtain an upper bound for
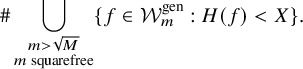 $$ \begin{align} \#\bigcup_{\substack{m>\sqrt{M}\\ m\;\mathrm{squarefree}}} \{f\in {\mathcal{W}}_{m}^{\mathrm{{gen}}}:H(f)<X\}. \end{align} $$
$$ \begin{align} \#\bigcup_{\substack{m>\sqrt{M}\\ m\;\mathrm{squarefree}}} \{f\in {\mathcal{W}}_{m}^{\mathrm{{gen}}}:H(f)<X\}. \end{align} $$
In §3.5, we defined a map
![]() $\sigma _m$
from the set of elements
$\sigma _m$
from the set of elements
![]() $f\in {\mathcal {W}}_m^{\mathrm {{{(2)}}}}$
with
$f\in {\mathcal {W}}_m^{\mathrm {{{(2)}}}}$
with
![]() $\gcd (m,f(0,1))=1$
to
$\gcd (m,f(0,1))=1$
to
![]() $W({\mathbb {Z}})$
such that
$W({\mathbb {Z}})$
such that
![]() $f_{\sigma _{m}(f)} = xf$
and
$f_{\sigma _{m}(f)} = xf$
and
![]() $ |q|(\sigma _{m}(f)) = m.$
For any
$ |q|(\sigma _{m}(f)) = m.$
For any
![]() $M>0$
, define the set
$M>0$
, define the set
![]() ${{\mathcal {L}}(M)}$
by
${{\mathcal {L}}(M)}$
by
 $$ \begin{align*} {{\mathcal{L}}(M)} :=\bigcup_{\substack{m>M\\m\;\mathrm{squarefree}}} \mathrm{{SL}}_{n+1}({\mathbb{Z}})\cdot \sigma_{m}({\mathcal{W}}_{m}^{\mathrm{{gen}}}). \end{align*} $$
$$ \begin{align*} {{\mathcal{L}}(M)} :=\bigcup_{\substack{m>M\\m\;\mathrm{squarefree}}} \mathrm{{SL}}_{n+1}({\mathbb{Z}})\cdot \sigma_{m}({\mathcal{W}}_{m}^{\mathrm{{gen}}}). \end{align*} $$
Then (36) is
![]() $\ll $
$\ll $
where
is as defined immediately after (16), where Y is now taken to be
![]() $X^{1/(n+1)}$
throughout this section. Moreover, exactly as in the paragraph leading up to (17), we break up
$X^{1/(n+1)}$
throughout this section. Moreover, exactly as in the paragraph leading up to (17), we break up
![]() ${\mathcal {I}}_X({{\mathcal {L}}(M)})$
into three parts – corresponding to the main body, the shallow cusp and the deep cusp – and again write
${\mathcal {I}}_X({{\mathcal {L}}(M)})$
into three parts – corresponding to the main body, the shallow cusp and the deep cusp – and again write
The rest of this section is dedicated to obtaining an upper bound on
![]() ${\mathcal {I}}_X({{\mathcal {L}}(M)} )$
. Every element
${\mathcal {I}}_X({{\mathcal {L}}(M)} )$
. Every element
![]() $(A,B)\in {{\mathcal {L}}(M)} $
satisfies
$(A,B)\in {{\mathcal {L}}(M)} $
satisfies
![]() $\det (B)=0$
since
$\det (B)=0$
since
![]() $f_{A,B}$
is divisible by x. In §4, we used vanishing conditions on the coefficients
$f_{A,B}$
is divisible by x. In §4, we used vanishing conditions on the coefficients
![]() $\{a_{ij},b_{ij}\}$
of W to estimate the number of integral pairs
$\{a_{ij},b_{ij}\}$
of W to estimate the number of integral pairs
![]() $(A,B)$
in skewed domains of
$(A,B)$
in skewed domains of
![]() $W({\mathbb {R}})$
. Now, since we also need to impose the condition that B has determinant
$W({\mathbb {R}})$
. Now, since we also need to impose the condition that B has determinant
![]() $0$
, we use the setup of §5 to count the number of such B’s in skewed bounded domains by fibering over the row space of B.
$0$
, we use the setup of §5 to count the number of such B’s in skewed bounded domains by fibering over the row space of B.
In §6.1, we thus further break up the three parts of
![]() ${\mathcal {I}}_X({{\mathcal {L}}(M)})$
into sums over row spaces of the singular matrix B. We also obtain some preliminary bounds on
${\mathcal {I}}_X({{\mathcal {L}}(M)})$
into sums over row spaces of the singular matrix B. We also obtain some preliminary bounds on
![]() ${\mathcal {I}}_X({{\mathcal {L}}(M)})$
and give some conditions that ensure that a pair
${\mathcal {I}}_X({{\mathcal {L}}(M)})$
and give some conditions that ensure that a pair
![]() $(A,B)$
has discriminant
$(A,B)$
has discriminant
![]() $0$
. In §6.2, §6.3 and §6.4, we then prove the desired upper bounds on
$0$
. In §6.2, §6.3 and §6.4, we then prove the desired upper bounds on
![]() ${\mathcal {I}}^{\mathrm {{main}}}_X({{\mathcal {L}}(M)})$
,
${\mathcal {I}}^{\mathrm {{main}}}_X({{\mathcal {L}}(M)})$
,
![]() ${\mathcal {I}}^{\mathrm {{scusp}}}_X({{\mathcal {L}}(M)})$
, and
${\mathcal {I}}^{\mathrm {{scusp}}}_X({{\mathcal {L}}(M)})$
, and
![]() ${\mathcal {I}}^{\mathrm {{dcusp}}}_X({{\mathcal {L}}(M)})$
, respectively. In conjunction with (35), (37) and Lemmas 6.1–6.2, this will yield Theorem 5(c).
${\mathcal {I}}^{\mathrm {{dcusp}}}_X({{\mathcal {L}}(M)})$
, respectively. In conjunction with (35), (37) and Lemmas 6.1–6.2, this will yield Theorem 5(c).
6.1 Setup and preliminary bounds
Coordinate systems, weight functions and summing over row spaces
Let
![]() $S({\mathbb {Z}})$
denote the set of
$S({\mathbb {Z}})$
denote the set of
![]() $(n+1)\times (n+1)$
integral symmetric matrices. For any primitive lattice
$(n+1)\times (n+1)$
integral symmetric matrices. For any primitive lattice
![]() $\Lambda $
of
$\Lambda $
of
![]() ${\mathbb {Z}}^{n+1}$
, let
${\mathbb {Z}}^{n+1}$
, let
![]() $S(\Lambda )$
denote the sublattice of
$S(\Lambda )$
denote the sublattice of
![]() $S({\mathbb {Z}})$
consisting of elements
$S({\mathbb {Z}})$
consisting of elements
![]() $B\in S({\mathbb {Z}})$
with row space contained in
$B\in S({\mathbb {Z}})$
with row space contained in
![]() $\Lambda $
. For
$\Lambda $
. For
![]() $L=(L_1,\ldots ,L_n)$
with
$L=(L_1,\ldots ,L_n)$
with
![]() $L_i\in {\mathbb {R}}$
and
$L_i\in {\mathbb {R}}$
and
![]() $L_1\leq L_2\leq \cdots \leq L_n$
and
$L_1\leq L_2\leq \cdots \leq L_n$
and
![]() $s\in T'$
, let
$s\in T'$
, let
![]() $\Sigma (L,s)$
denote the set of primitive lattices
$\Sigma (L,s)$
denote the set of primitive lattices
![]() $\Lambda \subset {\mathbb {Z}}^{n+1}$
of rank n such that the successive minima
$\Lambda \subset {\mathbb {Z}}^{n+1}$
of rank n such that the successive minima
![]() $\mu _1,\ldots ,\mu _n$
of
$\mu _1,\ldots ,\mu _n$
of
![]() $s^{-1}\Lambda $
satisfy
$s^{-1}\Lambda $
satisfy
![]() $L_1\leq \mu _i\leq 2L_i$
for each i. We define
$L_1\leq \mu _i\leq 2L_i$
for each i. We define
![]() ${\mathcal {S}}(L,s)\subset S({\mathbb {Z}})$
by
${\mathcal {S}}(L,s)\subset S({\mathbb {Z}})$
by
We next introduce coordinate systems and weight functions. Let
denote the set of coordinates of n-tuples of vectors in
![]() ${\mathbb {R}}^{n+1}$
. We define
${\mathbb {R}}^{n+1}$
. We define
The significance of
![]() $w_L$
is the following. Let
$w_L$
is the following. Let
![]() $\Lambda \in \Sigma (L,s)$
be a lattice with an integral basis
$\Lambda \in \Sigma (L,s)$
be a lattice with an integral basis
![]() $\{\ell _1,\ldots ,\ell _n\}$
such that
$\{\ell _1,\ldots ,\ell _n\}$
such that
![]() $\{s^{-1}\ell _1,\ldots ,s^{-1}\ell _n\}$
is a Minkowski-reduced basis for
$\{s^{-1}\ell _1,\ldots ,s^{-1}\ell _n\}$
is a Minkowski-reduced basis for
![]() $s^{-1}\Lambda $
. Then the jth coefficient of
$s^{-1}\Lambda $
. Then the jth coefficient of
![]() $\ell _i$
is
$\ell _i$
is
![]() $\ll L_it_j^{-1}=w_L(\ell _{ij})$
. In particular, for the absolute value of the jth coefficient of
$\ll L_it_j^{-1}=w_L(\ell _{ij})$
. In particular, for the absolute value of the jth coefficient of
![]() $\ell _i$
to be nonzero, we must have
$\ell _i$
to be nonzero, we must have
![]() $w_L(\ell _{ij})\gg 1$
. When L is implicit, we will write w in place of
$w_L(\ell _{ij})\gg 1$
. When L is implicit, we will write w in place of
![]() $w_L$
.
$w_L$
.
Let
![]() ${\mathcal {K}}$
denote the set of coefficients
${\mathcal {K}}$
denote the set of coefficients
![]() $\{a_{ij}:1\leq i\leq j\leq n+1\}$
, and recall the weight function
$\{a_{ij}:1\leq i\leq j\leq n+1\}$
, and recall the weight function
Define a partial order on
![]() ${\mathcal {K}}$
by setting
${\mathcal {K}}$
by setting
![]() $a_{ij}\lesssim a_{i'j'}$
if
$a_{ij}\lesssim a_{i'j'}$
if
![]() $i\leq i'$
and
$i\leq i'$
and
![]() $j\leq j'$
, and on
$j\leq j'$
, and on
![]() ${\mathcal {M}}$
by setting
${\mathcal {M}}$
by setting
![]() $\ell _{ij}\lesssim \ell _{i'j'}$
if
$\ell _{ij}\lesssim \ell _{i'j'}$
if
![]() $i\leq i'$
and
$i\leq i'$
and
![]() $j\leq j'$
. The significance of this partial order is that if
$j\leq j'$
. The significance of this partial order is that if
![]() $\alpha ,\beta \in {\mathcal {K}}$
with
$\alpha ,\beta \in {\mathcal {K}}$
with
![]() $\alpha \lesssim \beta $
and
$\alpha \lesssim \beta $
and
![]() $s\in T'$
, then
$s\in T'$
, then
![]() $w(\alpha )\ll w(\beta )$
and similarly,
$w(\alpha )\ll w(\beta )$
and similarly,
![]() $w_L(\alpha )\ll w_L(\beta )$
if
$w_L(\alpha )\ll w_L(\beta )$
if
![]() $\alpha ,\beta \in {\mathcal {M}}.$
$\alpha ,\beta \in {\mathcal {M}}.$
We say that a subset
![]() ${\mathcal {Z}}$
of
${\mathcal {Z}}$
of
![]() ${\mathcal {K}}\cup {\mathcal {M}}$
is saturated if for any
${\mathcal {K}}\cup {\mathcal {M}}$
is saturated if for any
![]() $\alpha \in {\mathcal {Z}}$
, all the
$\alpha \in {\mathcal {Z}}$
, all the
![]() $\alpha '\in {\mathcal {K}}\cup {\mathcal {M}}$
with
$\alpha '\in {\mathcal {K}}\cup {\mathcal {M}}$
with
![]() $\alpha '\lesssim \alpha $
are also contained in
$\alpha '\lesssim \alpha $
are also contained in
![]() ${\mathcal {Z}}$
.
${\mathcal {Z}}$
.
Let
![]() ${\mathcal {D}}\subset S({\mathbb {R}})$
be a bounded domain such that
${\mathcal {D}}\subset S({\mathbb {R}})$
be a bounded domain such that
![]() ${\mathcal {B}}\subset {\mathcal {D}}\times {\mathcal {D}}$
. We pick positive constants
${\mathcal {B}}\subset {\mathcal {D}}\times {\mathcal {D}}$
. We pick positive constants
![]() $c_{ij}$
for
$c_{ij}$
for
![]() $1\leq i\leq j\leq n+1$
and
$1\leq i\leq j\leq n+1$
and
![]() $c_i^{\prime }$
for
$c_i^{\prime }$
for
![]() $1\leq i\leq n$
such that
$1\leq i\leq n$
such that
-
(a) if
 $|Yw(a_{ij})|<c_{ij}$
, then the
$|Yw(a_{ij})|<c_{ij}$
, then the
 $a_{ij}$
–coordinate of any integral element in
$a_{ij}$
–coordinate of any integral element in
 $s(Y{\mathcal {D}})$
is
$s(Y{\mathcal {D}})$
is
 $0$
;
$0$
; -
(b) if
 $|w_L(\ell _{ij})|<c_j^{\prime }$
, then the jth coefficient of
$|w_L(\ell _{ij})|<c_j^{\prime }$
, then the jth coefficient of
 $\ell _i$
for any lattice
$\ell _i$
for any lattice
 $\Lambda \in \Sigma (L,s)$
is
$\Lambda \in \Sigma (L,s)$
is
 $0$
;
$0$
; -
(c)
 $c_i^{\prime }<c'$
for all
$c_i^{\prime }<c'$
for all
 $i=1,\ldots ,n$
, where
$i=1,\ldots ,n$
, where
 $c'$
is the constant in Lemma 5.6;
$c'$
is the constant in Lemma 5.6; -
(d)
 $c_1c_{g+1,g+1}\leq c_{g+1}^{\prime \,2}$
, where
$c_1c_{g+1,g+1}\leq c_{g+1}^{\prime \,2}$
, where
 $c_1$
is the constant in Proposition 5.4;
$c_1$
is the constant in Proposition 5.4; -
(e) for any
 $i\leq i'$
and
$i\leq i'$
and
 $j\leq j'$
, we have
$j\leq j'$
, we have
 $w(a_{ij})/c_{ij} \leq w(a_{i'j'})/c_{i'j'}$
and
$w(a_{ij})/c_{ij} \leq w(a_{i'j'})/c_{i'j'}$
and
 $w(\ell _{ij})/c_j^{\prime } \leq w(\ell _{i'j'})/c_{j'}^{\prime }.$
$w(\ell _{ij})/c_j^{\prime } \leq w(\ell _{i'j'})/c_{j'}^{\prime }.$
More explicitly, we choose
![]() $c_{n+1,n+1}$
and
$c_{n+1,n+1}$
and
![]() $c_n'$
to be sufficiently small and take
$c_n'$
to be sufficiently small and take
 $$ \begin{align*} \nonumber c_{ij} &= \Big(\sup_{s\in T'} \frac{w(a_{ij})}{w(a_{n+1,n+1})}\Big) c_{n+1,n+1}\quad\text{for }i\leq j\leq n+1;\\ \nonumber c_i^{\prime} &= \Big(\sup_{s\in T'} \frac{t_i^{-1}}{t_n^{-1}}\Big) c_n^{\prime}\quad\text{for }i\leq n. \end{align*} $$
$$ \begin{align*} \nonumber c_{ij} &= \Big(\sup_{s\in T'} \frac{w(a_{ij})}{w(a_{n+1,n+1})}\Big) c_{n+1,n+1}\quad\text{for }i\leq j\leq n+1;\\ \nonumber c_i^{\prime} &= \Big(\sup_{s\in T'} \frac{t_i^{-1}}{t_n^{-1}}\Big) c_n^{\prime}\quad\text{for }i\leq n. \end{align*} $$
For any nondecreasing n-tuple L of positive real numbers, and a saturated subset
![]() ${\mathcal {Z}}$
of
${\mathcal {Z}}$
of
![]() ${\mathcal {K}}\cup {\mathcal {M}}$
, we define the following subset
${\mathcal {K}}\cup {\mathcal {M}}$
, we define the following subset
![]() $T_{\mathcal {Z}}(L,Y)$
of
$T_{\mathcal {Z}}(L,Y)$
of
![]() $T'$
:
$T'$
:
 $$ \begin{align} T_{\mathcal{Z}}(L,Y) := \left\{s\in T'\left| \begin{array}{l} s_i\ll X^\Theta\;\; \forall i\in\{1,\ldots,n\}\\[.1in] \mathrm{for}\;a_{ij}\in{\mathcal{K}},\;|Yw(a_{ij})|<c_{ij} \;\mathrm{{iff}}\;a_{ij}\in {\mathcal{Z}}\cap{\mathcal{K}}\\[.1in] \mathrm{for}\;\ell_{ij}\in{\mathcal{M}},\;|w_L(\ell_{ij})|<c_j^{\prime} \;\mathrm{{iff}}\;\ell_{ij}\in {\mathcal{Z}}\cap{\mathcal{M}} \end{array} \right.\right\}, \end{align} $$
$$ \begin{align} T_{\mathcal{Z}}(L,Y) := \left\{s\in T'\left| \begin{array}{l} s_i\ll X^\Theta\;\; \forall i\in\{1,\ldots,n\}\\[.1in] \mathrm{for}\;a_{ij}\in{\mathcal{K}},\;|Yw(a_{ij})|<c_{ij} \;\mathrm{{iff}}\;a_{ij}\in {\mathcal{Z}}\cap{\mathcal{K}}\\[.1in] \mathrm{for}\;\ell_{ij}\in{\mathcal{M}},\;|w_L(\ell_{ij})|<c_j^{\prime} \;\mathrm{{iff}}\;\ell_{ij}\in {\mathcal{Z}}\cap{\mathcal{M}} \end{array} \right.\right\}, \end{align} $$
where
![]() $\Theta $
is the absolute constant from Lemma 4.7.
$\Theta $
is the absolute constant from Lemma 4.7.
For X, Y, L,
![]() ${\mathcal {Z}}$
as above and any subset
${\mathcal {Z}}$
as above and any subset
![]() ${\mathcal {L}}$
of
${\mathcal {L}}$
of
![]() $W({\mathbb {Z}})$
, we define the quantity
$W({\mathbb {Z}})$
, we define the quantity
In the proof of Theorem 5.1, we showed that unless
![]() $Y^{-\Theta _1}<L_1$
and
$Y^{-\Theta _1}<L_1$
and
![]() $Y^{\Theta _2}>L_n$
for some absolute positive constants
$Y^{\Theta _2}>L_n$
for some absolute positive constants
![]() $\Theta _1$
and
$\Theta _1$
and
![]() $\Theta _2$
, we have
$\Theta _2$
, we have
![]() ${\mathcal {S}}(L,s)=\emptyset $
, which implies that
${\mathcal {S}}(L,s)=\emptyset $
, which implies that
![]() $N({{\mathcal {L}}(M)} ,L,{\mathcal {Z}},X)=0$
. Therefore,
$N({{\mathcal {L}}(M)} ,L,{\mathcal {Z}},X)=0$
. Therefore,
where the inner sum is over saturated subsets
![]() ${\mathcal {Z}}$
of
${\mathcal {Z}}$
of
![]() ${\mathcal {K}}\cup {\mathcal {M}}$
, and the outer sum is over n-tuples
${\mathcal {K}}\cup {\mathcal {M}}$
, and the outer sum is over n-tuples
![]() $L=(L_1,\ldots ,L_n)$
with
$L=(L_1,\ldots ,L_n)$
with
![]() $L_1\leq L_2\leq \cdots \leq L_n$
that partition the region
$L_1\leq L_2\leq \cdots \leq L_n$
that partition the region
![]() $\{(\mu _1,\ldots ,\mu _n)\in [Y^{-\Theta _1},Y^{\Theta _2}]^n:\mu _1\leq \ldots \leq \mu _n\}$
into dyadic ranges.
$\{(\mu _1,\ldots ,\mu _n)\in [Y^{-\Theta _1},Y^{\Theta _2}]^n:\mu _1\leq \ldots \leq \mu _n\}$
into dyadic ranges.
We may therefore bound the main-body, the shallow-cusp and the deep-cusp parts of
![]() ${\mathcal {I}}_X({{\mathcal {L}}(M)} )$
in terms of sums over
${\mathcal {I}}_X({{\mathcal {L}}(M)} )$
in terms of sums over
![]() $N({{\mathcal {L}}(M)} ,L,{\mathcal {Z}},X)$
. We have
$N({{\mathcal {L}}(M)} ,L,{\mathcal {Z}},X)$
. We have
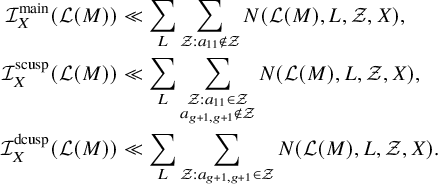 $$ \begin{align} {\mathcal{I}}_X^{\mathrm{{main}}}({{\mathcal{L}}(M)} )&\ll \sum_L\sum_{{\mathcal{Z}}:a_{11}\not\in{\mathcal{Z}}}N({{\mathcal{L}}(M)} ,L,{\mathcal{Z}},X), \nonumber\\ {\mathcal{I}}_X^{\mathrm{{scusp}}}({{\mathcal{L}}(M)} )&\ll \sum_L\sum_{\substack{{\mathcal{Z}}:a_{11}\in{\mathcal{Z}}\\a_{g+1,g+1}\not\in{\mathcal{Z}}}}N({{\mathcal{L}}(M)} ,L,{\mathcal{Z}},X), \\ {\mathcal{I}}_X^{\mathrm{{dcusp}}}({{\mathcal{L}}(M)} )&\ll \sum_L\sum_{{\mathcal{Z}}:a_{g+1,g+1}\in{\mathcal{Z}}}N({{\mathcal{L}}(M)} ,L,{\mathcal{Z}},X). \nonumber\end{align} $$
$$ \begin{align} {\mathcal{I}}_X^{\mathrm{{main}}}({{\mathcal{L}}(M)} )&\ll \sum_L\sum_{{\mathcal{Z}}:a_{11}\not\in{\mathcal{Z}}}N({{\mathcal{L}}(M)} ,L,{\mathcal{Z}},X), \nonumber\\ {\mathcal{I}}_X^{\mathrm{{scusp}}}({{\mathcal{L}}(M)} )&\ll \sum_L\sum_{\substack{{\mathcal{Z}}:a_{11}\in{\mathcal{Z}}\\a_{g+1,g+1}\not\in{\mathcal{Z}}}}N({{\mathcal{L}}(M)} ,L,{\mathcal{Z}},X), \\ {\mathcal{I}}_X^{\mathrm{{dcusp}}}({{\mathcal{L}}(M)} )&\ll \sum_L\sum_{{\mathcal{Z}}:a_{g+1,g+1}\in{\mathcal{Z}}}N({{\mathcal{L}}(M)} ,L,{\mathcal{Z}},X). \nonumber\end{align} $$
A preliminary upper bound
We now prove some preliminary results on
![]() $N({{\mathcal {L}}(1)} ,L,{\mathcal {Z}},X))$
. We start with an upper bound on
$N({{\mathcal {L}}(1)} ,L,{\mathcal {Z}},X))$
. We start with an upper bound on
![]() $N({{\mathcal {L}}(1)} ,L,{\mathcal {Z}},X)$
, which also bounds
$N({{\mathcal {L}}(1)} ,L,{\mathcal {Z}},X)$
, which also bounds
![]() $N({{\mathcal {L}}(M)} ,L,{\mathcal {Z}},X)$
by directly counting the number of possible A’s and then using the results of §5 to count B’s. For a saturated subset
$N({{\mathcal {L}}(M)} ,L,{\mathcal {Z}},X)$
by directly counting the number of possible A’s and then using the results of §5 to count B’s. For a saturated subset
![]() ${\mathcal {Z}}$
of
${\mathcal {Z}}$
of
![]() ${\mathcal {K}}\cup {\mathcal {M}}$
, define
${\mathcal {K}}\cup {\mathcal {M}}$
, define
In what follows, the n-tuple L will be clear from the context, and we simply write w in place of
![]() $w_L$
.
$w_L$
.
Proposition 6.3. Suppose that
![]() ${\mathcal {Z}}$
is a saturated subset of
${\mathcal {Z}}$
is a saturated subset of
![]() ${\mathcal {K}}\cup {\mathcal {M}}$
. Then
${\mathcal {K}}\cup {\mathcal {M}}$
. Then
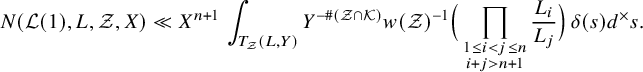 $$ \begin{align} N({{\mathcal{L}}(1)} ,L,{\mathcal{Z}},X) \ll X^{n+1}\,\int_{T_{\mathcal{Z}}(L,Y)} Y^{-\#({\mathcal{Z}}\cap{\mathcal{K}})}w({\mathcal{Z}})^{-1} \Big(\prod_{\substack{1\leq i< j\leq n\\ i+j> n+1}}\frac{L_i}{L_j}\Big) \,\delta(s)d^\times s. \end{align} $$
$$ \begin{align} N({{\mathcal{L}}(1)} ,L,{\mathcal{Z}},X) \ll X^{n+1}\,\int_{T_{\mathcal{Z}}(L,Y)} Y^{-\#({\mathcal{Z}}\cap{\mathcal{K}})}w({\mathcal{Z}})^{-1} \Big(\prod_{\substack{1\leq i< j\leq n\\ i+j> n+1}}\frac{L_i}{L_j}\Big) \,\delta(s)d^\times s. \end{align} $$
Proof. By Proposition 4.1, the number of elements
![]() $A\in s(Y{\mathcal {D}})\cap S({\mathbb {Z}})$
is
$A\in s(Y{\mathcal {D}})\cap S({\mathbb {Z}})$
is
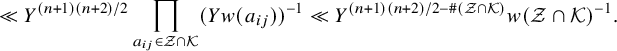 $$ \begin{align} \ll Y^{(n+1)(n+2)/2}\prod_{a_{ij}\in {\mathcal{Z}}\cap{\mathcal{K}}}(Yw(a_{ij}))^{-1} \ll Y^{(n+1)(n+2)/2-\#({\mathcal{Z}}\cap{\mathcal{K}})} w({\mathcal{Z}}\cap{\mathcal{K}})^{-1}. \end{align} $$
$$ \begin{align} \ll Y^{(n+1)(n+2)/2}\prod_{a_{ij}\in {\mathcal{Z}}\cap{\mathcal{K}}}(Yw(a_{ij}))^{-1} \ll Y^{(n+1)(n+2)/2-\#({\mathcal{Z}}\cap{\mathcal{K}})} w({\mathcal{Z}}\cap{\mathcal{K}})^{-1}. \end{align} $$
By the definition of
![]() $T_{\mathcal {Z}}(L,Y)$
, it follows from (29) that for every
$T_{\mathcal {Z}}(L,Y)$
, it follows from (29) that for every
![]() $s\in T_{\mathcal {Z}}(L,Y)$
, we have
$s\in T_{\mathcal {Z}}(L,Y)$
, we have
 $$ \begin{align} \#\Sigma(L,s) \ll (L_1\cdots L_n)^{n+1} w({\mathcal{Z}}\cap{\mathcal{M}})^{-1} \prod_{1\leq i<j\leq n}\frac{L_i}{L_j}. \end{align} $$
$$ \begin{align} \#\Sigma(L,s) \ll (L_1\cdots L_n)^{n+1} w({\mathcal{Z}}\cap{\mathcal{M}})^{-1} \prod_{1\leq i<j\leq n}\frac{L_i}{L_j}. \end{align} $$
For each
![]() $\Lambda \in \Sigma (L,s)$
, Proposition 5.5 implies that the number of integral symmetric matrices
$\Lambda \in \Sigma (L,s)$
, Proposition 5.5 implies that the number of integral symmetric matrices
![]() $B\in s(Y{\mathcal {D}})$
whose row space is contained in
$B\in s(Y{\mathcal {D}})$
whose row space is contained in
![]() $\Lambda $
is
$\Lambda $
is
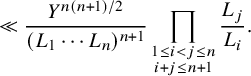 $$ \begin{align} \ll \frac{Y^{n(n+1)/2}}{(L_1\cdots L_n)^{n+1}} \prod_{\substack{1\leq i< j\leq n\\i+j\leq n+1}} \frac{L_j}{L_i}. \end{align} $$
$$ \begin{align} \ll \frac{Y^{n(n+1)/2}}{(L_1\cdots L_n)^{n+1}} \prod_{\substack{1\leq i< j\leq n\\i+j\leq n+1}} \frac{L_j}{L_i}. \end{align} $$
Combining (42), (43) and (44), and recalling that
![]() $X = Y^{n+1}$
, gives (41).
$X = Y^{n+1}$
, gives (41).
Conditions for vanishing discriminant
Next, we give some conditions on
![]() ${\mathcal {Z}}$
that ensure
${\mathcal {Z}}$
that ensure
![]() $N({{\mathcal {L}}(1)} ,L,{\mathcal {Z}},X) = 0$
. We start with the following algebraic result that gives sufficient conditions on a pair
$N({{\mathcal {L}}(1)} ,L,{\mathcal {Z}},X) = 0$
. We start with the following algebraic result that gives sufficient conditions on a pair
![]() $(A,B)\in W({\mathbb {C}})$
that ensure it has discriminant
$(A,B)\in W({\mathbb {C}})$
that ensure it has discriminant
![]() $0$
.
$0$
.
Lemma 6.4. Suppose that
![]() $(A,B)$
is an element of
$(A,B)$
is an element of
![]() $W({\mathbb {C}})$
such that one of the following three conditions are satisfied:
$W({\mathbb {C}})$
such that one of the following three conditions are satisfied:
-
(a) The kernel of B has dimension at least
 $2$
.
$2$
. -
(b) There is a nonzero vector
 $v\in {\mathbb {C}}^{n+1}$
that is in the kernel of B and isotropic with respect to A.
$v\in {\mathbb {C}}^{n+1}$
that is in the kernel of B and isotropic with respect to A. -
(c) There exists
 $k\in \{ 1,\ldots ,g+1\}$
such that
$k\in \{ 1,\ldots ,g+1\}$
such that
 $a_{ij} = b_{ij} = 0$
for all
$a_{ij} = b_{ij} = 0$
for all
 $1\leq i\leq k$
and all
$1\leq i\leq k$
and all
 $1\leq j\leq n+1-k$
.
$1\leq j\leq n+1-k$
.
Then
![]() $\Delta (A,B) = 0$
.
$\Delta (A,B) = 0$
.
Proof. This is a standard result in the algebraic geometric theory of pencils of quadrics. We give another proof using the explicit formula for
![]() $f(x,y) = f_{A,B}(x,y).$
The claim regarding Condition (c) is Lemma 4.6. If the kernel of B has dimension at least
$f(x,y) = f_{A,B}(x,y).$
The claim regarding Condition (c) is Lemma 4.6. If the kernel of B has dimension at least
![]() $2$
, then the quadratic form defined by A restricted to the kernel of B admits a nonzero isotropic vector in
$2$
, then the quadratic form defined by A restricted to the kernel of B admits a nonzero isotropic vector in
![]() ${\mathbb {C}}^{n+1}$
. Thus Condition (a) implies Condition (b). Suppose now that Condition (b) is satisfied. Then the
${\mathbb {C}}^{n+1}$
. Thus Condition (a) implies Condition (b). Suppose now that Condition (b) is satisfied. Then the
![]() $y^{n+1}$
-coefficient of
$y^{n+1}$
-coefficient of
![]() $f(x,y)$
is
$f(x,y)$
is
![]() $0$
since B is singular. The
$0$
since B is singular. The
![]() $xy^n$
-coefficient of
$xy^n$
-coefficient of
![]() $f(x,y)$
equals, up to sign, the alternating sum of the determinants of the matrices obtained by replacing the i-th column of B by the i-th column of A. By translating the vector v to
$f(x,y)$
equals, up to sign, the alternating sum of the determinants of the matrices obtained by replacing the i-th column of B by the i-th column of A. By translating the vector v to
![]() $(1,0,0,\ldots ,0)$
using an element of
$(1,0,0,\ldots ,0)$
using an element of
![]() $\mathrm {{SL}}_{n+1}({\mathbb {C}})$
, we may assume that the first column (and row) of B is
$\mathrm {{SL}}_{n+1}({\mathbb {C}})$
, we may assume that the first column (and row) of B is
![]() $0$
and the
$0$
and the
![]() $(1,1)$
-entry of A is
$(1,1)$
-entry of A is
![]() $0$
. It is then easy to see that the determinant of the matrix obtained by replacing the i-th column of B by the i-th column of A is
$0$
. It is then easy to see that the determinant of the matrix obtained by replacing the i-th column of B by the i-th column of A is
![]() $0$
for any i. Hence,
$0$
for any i. Hence,
![]() $\Delta (A,B) = \Delta (f) = 0$
.
$\Delta (A,B) = \Delta (f) = 0$
.
We now translate these conditions into the vanishing of
![]() $N({{\mathcal {L}}(1)} ,L,{\mathcal {Z}},X)$
for certain sets
$N({{\mathcal {L}}(1)} ,L,{\mathcal {Z}},X)$
for certain sets
![]() ${\mathcal {Z}}$
. To this end, define the set
${\mathcal {Z}}$
. To this end, define the set
![]() ${\mathcal {Z}}_1\subset {\mathcal {K}}\cup {\mathcal {M}}$
by
${\mathcal {Z}}_1\subset {\mathcal {K}}\cup {\mathcal {M}}$
by
Lemma 6.5. Let
![]() ${\mathcal {Z}}$
be a saturated subset of
${\mathcal {Z}}$
be a saturated subset of
![]() ${\mathcal {K}}\cup {\mathcal {M}}$
satisfying one of the following two conditions:
${\mathcal {K}}\cup {\mathcal {M}}$
satisfying one of the following two conditions:
-
(a) The set
 ${\mathcal {Z}}$
is not contained in
${\mathcal {Z}}$
is not contained in
 ${\mathcal {Z}}_1$
.
${\mathcal {Z}}_1$
. -
(b) There exists
 $k\in \{1,\ldots ,g+1\}$
such that
$k\in \{1,\ldots ,g+1\}$
such that
 $a_{kk}\in {\mathcal {Z}}$
and
$a_{kk}\in {\mathcal {Z}}$
and
 $\ell _{n+1-k,k}\in {\mathcal {Z}}$
.
$\ell _{n+1-k,k}\in {\mathcal {Z}}$
.
Then
![]() $N({{\mathcal {L}}(1)} ,L,{\mathcal {Z}},X) = 0$
.
$N({{\mathcal {L}}(1)} ,L,{\mathcal {Z}},X) = 0$
.
Proof. If
![]() ${\mathcal {Z}}$
contains some
${\mathcal {Z}}$
contains some
![]() $\ell _{ij}\notin {\mathcal {Z}}_1$
, then for every
$\ell _{ij}\notin {\mathcal {Z}}_1$
, then for every
![]() $s\in T_{\mathcal {Z}}(L,Y)$
, the set
$s\in T_{\mathcal {Z}}(L,Y)$
, the set
![]() $\Sigma (L,s)$
(and hence
$\Sigma (L,s)$
(and hence
![]() ${\mathcal {S}}(L,s)$
) is empty by Lemma 5.6. This implies that
${\mathcal {S}}(L,s)$
) is empty by Lemma 5.6. This implies that
![]() $N({{\mathcal {L}}(1)} ,L,{\mathcal {Z}},X)=0$
. If
$N({{\mathcal {L}}(1)} ,L,{\mathcal {Z}},X)=0$
. If
![]() ${\mathcal {Z}}$
contains some
${\mathcal {Z}}$
contains some
![]() $a_{ij}\notin {\mathcal {Z}}_1$
, then every integral
$a_{ij}\notin {\mathcal {Z}}_1$
, then every integral
![]() $(A,B)\in s(Y{\mathcal {D}}\times s(Y{\mathcal {D}})$
has discriminant
$(A,B)\in s(Y{\mathcal {D}}\times s(Y{\mathcal {D}})$
has discriminant
![]() $0$
by Condition (c) of Lemma 6.4. Once again, this implies that
$0$
by Condition (c) of Lemma 6.4. Once again, this implies that
![]() $N({{\mathcal {L}}(1)} ,L,{\mathcal {Z}},X)=0$
.
$N({{\mathcal {L}}(1)} ,L,{\mathcal {Z}},X)=0$
.
Let k be an integer satisfying Condition (b) of the lemma, and let
![]() $s\in T_{\mathcal {Z}}(L,Y)$
. Let
$s\in T_{\mathcal {Z}}(L,Y)$
. Let
![]() $(A,B)$
be such that
$(A,B)$
be such that
![]() $A\in s(Y{\mathcal {D}})$
and
$A\in s(Y{\mathcal {D}})$
and
![]() $B\in {\mathcal {S}}(L,s)$
. Since
$B\in {\mathcal {S}}(L,s)$
. Since
![]() $\ell _{n+1-k,k}\in {\mathcal {Z}}$
, it follows that there exists a nonzero vector
$\ell _{n+1-k,k}\in {\mathcal {Z}}$
, it follows that there exists a nonzero vector
![]() $v\in {\mathbb {C}}^{n+1}$
of the form
$v\in {\mathbb {C}}^{n+1}$
of the form
![]() $(v_1,\ldots ,v_k,0,\ldots ,0)$
that is in the kernel of B. Since
$(v_1,\ldots ,v_k,0,\ldots ,0)$
that is in the kernel of B. Since
![]() $a_{kk}\in {\mathcal {Z}}$
, it follows that v is isotropic with respect to A. By Condition (b) of Lemma 6.4, it follows that
$a_{kk}\in {\mathcal {Z}}$
, it follows that v is isotropic with respect to A. By Condition (b) of Lemma 6.4, it follows that
![]() $\Delta (A,B) = 0$
, implying that
$\Delta (A,B) = 0$
, implying that
![]() $N({{\mathcal {L}}(1)} ,L,{\mathcal {Z}},X)=0$
, as desired.
$N({{\mathcal {L}}(1)} ,L,{\mathcal {Z}},X)=0$
, as desired.
6.2 Bounding the number of distinguished elements in the main body
In this subsection, we bound the number of distinguished elements in the main body:
Theorem 6.6. We have
![]() ${\mathcal {I}}_X^{\mathrm {{main}}}({{\mathcal {L}}(1)} )=O\big (X^{n+1-1/(4n) + \epsilon }\big )$
.
${\mathcal {I}}_X^{\mathrm {{main}}}({{\mathcal {L}}(1)} )=O\big (X^{n+1-1/(4n) + \epsilon }\big )$
.
As
![]() ${{\mathcal {L}}(M)} \subset {{\mathcal {L}}(1)} $
for
${{\mathcal {L}}(M)} \subset {{\mathcal {L}}(1)} $
for
![]() $M\geq 1$
, it follows that
$M\geq 1$
, it follows that
![]() ${\mathcal {I}}_X^{\mathrm {{main}}}({{\mathcal {L}}(M)} )$
satisfies the same bound.
${\mathcal {I}}_X^{\mathrm {{main}}}({{\mathcal {L}}(M)} )$
satisfies the same bound.
We will use the Selberg sieve to show that distinsuished elements are negligible in number in the main body. However, applying the Selberg sieve requires asymptotics along with a power saving error term. Our methods in §5 do not yield such results.
Hence, we will instead fiber over
![]() $B\in s(Y{\mathcal {D}})\cap S({\mathbb {Z}})$
having determinant
$B\in s(Y{\mathcal {D}})\cap S({\mathbb {Z}})$
having determinant
![]() $0$
, apply the Selberg sieve to prove that there are negligibly many
$0$
, apply the Selberg sieve to prove that there are negligibly many
![]() $A\in s(Y{\mathcal {D}})\cap S({\mathbb {Z}})$
such that
$A\in s(Y{\mathcal {D}})\cap S({\mathbb {Z}})$
such that
![]() $(A,B)$
is distinguished, and then bound the number of possible B’s using the results of Section 5. To carry out the middle step, we require the following lower bound on the number of nondistinguished elements modulo primes p that is independent of p and B.
$(A,B)$
is distinguished, and then bound the number of possible B’s using the results of Section 5. To carry out the middle step, we require the following lower bound on the number of nondistinguished elements modulo primes p that is independent of p and B.
Lemma 6.7. Let
![]() $B_0$
be an element in
$B_0$
be an element in
![]() $S({\mathbb {F}}_p)$
with
$S({\mathbb {F}}_p)$
with
![]() ${\mathbb {F}}_p$
-rank n. Let
${\mathbb {F}}_p$
-rank n. Let
![]() $S_{B_0}^{\mathrm {{ndist}}}({\mathbb {F}}_p)$
denote the set of elements
$S_{B_0}^{\mathrm {{ndist}}}({\mathbb {F}}_p)$
denote the set of elements
![]() $A\in S({\mathbb {F}}_p)$
such that
$A\in S({\mathbb {F}}_p)$
such that
![]() $(A,B_0)$
has nonzero discriminant and A and
$(A,B_0)$
has nonzero discriminant and A and
![]() $B_0$
do not have a common isotropic
$B_0$
do not have a common isotropic
![]() $(g+1)$
-dimensional subspace. Then
$(g+1)$
-dimensional subspace. Then
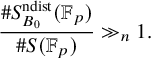 $$ \begin{align*} \frac{\#S_{B_0}^{\mathrm{{ndist}}}({\mathbb{F}}_p)}{\#S({\mathbb{F}}_p)}\gg_n 1. \end{align*} $$
$$ \begin{align*} \frac{\#S_{B_0}^{\mathrm{{ndist}}}({\mathbb{F}}_p)}{\#S({\mathbb{F}}_p)}\gg_n 1. \end{align*} $$
Proof. For an element
![]() $B\in S({\mathbb {F}}_p)$
with
$B\in S({\mathbb {F}}_p)$
with
![]() ${\mathbb {F}}_p$
-rank n and kernel spanned by v, let
${\mathbb {F}}_p$
-rank n and kernel spanned by v, let
![]() $d(B)$
denote the discriminant of the corresponding quadratic form on
$d(B)$
denote the discriminant of the corresponding quadratic form on
![]() ${\mathbb {F}}_p^{n+1}/({\mathbb {F}}_p v)$
. If
${\mathbb {F}}_p^{n+1}/({\mathbb {F}}_p v)$
. If
![]() $B_1,B_2\in S({\mathbb {F}}_p)$
have
$B_1,B_2\in S({\mathbb {F}}_p)$
have
![]() ${\mathbb {F}}_p$
-rank n and
${\mathbb {F}}_p$
-rank n and
![]() $d(B_1)/d(B_2)\in {\mathbb {F}}_p^{\times 2}$
, then
$d(B_1)/d(B_2)\in {\mathbb {F}}_p^{\times 2}$
, then
![]() $B_1$
and
$B_1$
and
![]() $B_2$
are
$B_2$
are
![]() $\mathrm {{SL}}_{n+1}({\mathbb {F}}_p)$
-equivalent. Indeed, by using
$\mathrm {{SL}}_{n+1}({\mathbb {F}}_p)$
-equivalent. Indeed, by using
![]() $\mathrm {{SL}}_{n+1}({\mathbb {F}}_p)$
transformations, we may assume the last row and columns of
$\mathrm {{SL}}_{n+1}({\mathbb {F}}_p)$
transformations, we may assume the last row and columns of
![]() $B_1$
and
$B_1$
and
![]() $B_2$
are all
$B_2$
are all
![]() $0$
. The nondegenerate forms defined by the top left
$0$
. The nondegenerate forms defined by the top left
![]() $n\times n$
blocks of
$n\times n$
blocks of
![]() $B_1$
and
$B_1$
and
![]() $B_2$
have discriminants
$B_2$
have discriminants
![]() $d(B_1)$
and
$d(B_1)$
and
![]() $d(B_2)$
, which are in the same quadratic residue class. Hence, they are equivalent via an element
$d(B_2)$
, which are in the same quadratic residue class. Hence, they are equivalent via an element
![]() $\gamma \in \mathrm {{GL}}_n({\mathbb {F}}_p)$
. Expanding
$\gamma \in \mathrm {{GL}}_n({\mathbb {F}}_p)$
. Expanding
![]() $\gamma $
to an element in
$\gamma $
to an element in
![]() $\mathrm {{SL}}_{n+1}({\mathbb {F}}_p)$
by appending an additional row and column whose entries are all
$\mathrm {{SL}}_{n+1}({\mathbb {F}}_p)$
by appending an additional row and column whose entries are all
![]() $0$
, except for the
$0$
, except for the
![]() $(n+1,n+1)$
-entry which is
$(n+1,n+1)$
-entry which is
![]() $\det \gamma ^{-1}$
, gives an element in
$\det \gamma ^{-1}$
, gives an element in
![]() $\mathrm {{SL}}_{n+1}({\mathbb {F}}_p)$
that takes
$\mathrm {{SL}}_{n+1}({\mathbb {F}}_p)$
that takes
![]() $B_1$
to
$B_1$
to
![]() $B_2$
.
$B_2$
.
Let
![]() $B_0\in S({\mathbb {F}}_p)$
have
$B_0\in S({\mathbb {F}}_p)$
have
![]() ${\mathbb {F}}_p$
-rank n. For each binary n-ic form
${\mathbb {F}}_p$
-rank n. For each binary n-ic form
![]() $f(x,y) = a_0x^n + \cdots + a_ny^n$
over
$f(x,y) = a_0x^n + \cdots + a_ny^n$
over
![]() ${\mathbb {F}}_p$
that splits completely over
${\mathbb {F}}_p$
that splits completely over
![]() ${\mathbb {F}}_p$
such that
${\mathbb {F}}_p$
such that
![]() $\Delta (xf(x,y))\neq 0$
and
$\Delta (xf(x,y))\neq 0$
and
![]() $a_0\neq 0$
, we construct a nondistinguished element
$a_0\neq 0$
, we construct a nondistinguished element
![]() $(A_0,B_0)$
with
$(A_0,B_0)$
with
![]() $f_{A_0,B_0}=xf(x,y)$
. Let f be such a form. Then
$f_{A_0,B_0}=xf(x,y)$
. Let f be such a form. Then
![]() $a_n\neq 0$
. Let
$a_n\neq 0$
. Let
![]() $\alpha = d(B_0)/a_n$
. As noted in §3.1, there exist at least two (in fact
$\alpha = d(B_0)/a_n$
. As noted in §3.1, there exist at least two (in fact
![]() $2^{n-1}$
)
$2^{n-1}$
)
![]() $\mathrm {{SL}}_n({\mathbb {F}}_p)$
-orbits of
$\mathrm {{SL}}_n({\mathbb {F}}_p)$
-orbits of
![]() $(A,B)\in W_n({\mathbb {F}}_p)$
such that
$(A,B)\in W_n({\mathbb {F}}_p)$
such that
![]() $f_{A,B} = \alpha f(x,y)$
. Pick two inequivalent representatives
$f_{A,B} = \alpha f(x,y)$
. Pick two inequivalent representatives
![]() $(A_1,B_1)$
and
$(A_1,B_1)$
and
![]() $(A_2,B_2)$
. Let
$(A_2,B_2)$
. Let
![]() $A_1'$
and
$A_1'$
and
![]() $A_2'$
be the
$A_2'$
be the
![]() $(n+1)$
-ary quadratic forms obtained from
$(n+1)$
-ary quadratic forms obtained from
![]() $A_1$
and
$A_1$
and
![]() $A_2$
, respectively, by appending an additional row and column whose entries are all
$A_2$
, respectively, by appending an additional row and column whose entries are all
![]() $0$
except for the
$0$
except for the
![]() $(n+1,n+1)$
-entry which is
$(n+1,n+1)$
-entry which is
![]() $\alpha ^{-1}$
. Let
$\alpha ^{-1}$
. Let
![]() $B_1'$
and
$B_1'$
and
![]() $B_2'$
be the
$B_2'$
be the
![]() $(n+1)$
-ary quadratic forms obtained from
$(n+1)$
-ary quadratic forms obtained from
![]() $B_1$
and
$B_1$
and
![]() $B_2$
, respectively, by appending an additional row and column whose entries are all
$B_2$
, respectively, by appending an additional row and column whose entries are all
![]() $0$
. Then
$0$
. Then
![]() $f_{A_1',B_1'} = f_{A_2',B_2'} = xf(x,y).$
Since
$f_{A_1',B_1'} = f_{A_2',B_2'} = xf(x,y).$
Since
![]() $(A_1,B_1)$
and
$(A_1,B_1)$
and
![]() $(A_2,B_2)$
are
$(A_2,B_2)$
are
![]() $\mathrm {{SL}}_n({\mathbb {F}}_p)$
-inequivalent, it follows that
$\mathrm {{SL}}_n({\mathbb {F}}_p)$
-inequivalent, it follows that
![]() $(A_1',B_1')$
and
$(A_1',B_1')$
and
![]() $(A_2',B_2')$
are
$(A_2',B_2')$
are
![]() $\mathrm {{SL}}_{n+1}({\mathbb {F}}_p)$
-inequivalent. Hence, without loss of generality, we may assume that
$\mathrm {{SL}}_{n+1}({\mathbb {F}}_p)$
-inequivalent. Hence, without loss of generality, we may assume that
![]() $(A_1',B_1')$
is nondistinguished. Now
$(A_1',B_1')$
is nondistinguished. Now
![]() $d(B_1')=\alpha a_n = d(B_0)$
, and so there exists
$d(B_1')=\alpha a_n = d(B_0)$
, and so there exists
![]() $\gamma \in \mathrm {{SL}}_{n+1}({\mathbb {F}}_p)$
such that
$\gamma \in \mathrm {{SL}}_{n+1}({\mathbb {F}}_p)$
such that
![]() $\gamma B_1'\gamma ^t = B_0$
. Then
$\gamma B_1'\gamma ^t = B_0$
. Then
![]() $A_0 = \gamma A_1'\gamma ^t$
does the job.
$A_0 = \gamma A_1'\gamma ^t$
does the job.
We complete the proof of the lemma via the orbit-stabilizer theorem. By the above construction, there are
![]() $\gg _n p^{n+1}$
binary
$\gg _n p^{n+1}$
binary
![]() $(n+1)$
-ic forms
$(n+1)$
-ic forms
![]() $xf(x,y)$
, with
$xf(x,y)$
, with
![]() $\Delta (xf(x,y))\neq 0$
and
$\Delta (xf(x,y))\neq 0$
and
![]() $a_0\neq 0$
, such that there exists an element
$a_0\neq 0$
, such that there exists an element
![]() $A\in S({\mathbb {F}}_p)$
with
$A\in S({\mathbb {F}}_p)$
with
![]() $f_{A,B_0}=xf(x,y)$
and
$f_{A,B_0}=xf(x,y)$
and
![]() $(A,B_0)$
nondistinguished. The group
$(A,B_0)$
nondistinguished. The group
![]() $G_{B_0}({\mathbb {F}}_p) = \{\gamma \in \mathrm {{SL}}_{n+1}({\mathbb {F}}_p)\colon \gamma B_0\gamma ^t = B_0\}$
acts on the set of such A with stabilizer of size
$G_{B_0}({\mathbb {F}}_p) = \{\gamma \in \mathrm {{SL}}_{n+1}({\mathbb {F}}_p)\colon \gamma B_0\gamma ^t = B_0\}$
acts on the set of such A with stabilizer of size
![]() $\# J_{xf}[2]({\mathbb {F}}_p)$
, where
$\# J_{xf}[2]({\mathbb {F}}_p)$
, where
![]() $J_{xf}$
is the Jacobian of the hyperelliptic curve defined by
$J_{xf}$
is the Jacobian of the hyperelliptic curve defined by
![]() $z^2 = xf(x,y)y$
. Any element of
$z^2 = xf(x,y)y$
. Any element of
![]() $\gamma \in G_{B_0}({\mathbb {F}}_p)$
preserves the kernel
$\gamma \in G_{B_0}({\mathbb {F}}_p)$
preserves the kernel
![]() ${\mathbb {F}}_p v$
of
${\mathbb {F}}_p v$
of
![]() $B_0$
and stabilizes the nondegenerate form
$B_0$
and stabilizes the nondegenerate form
![]() $b_0$
on
$b_0$
on
![]() ${\mathbb {F}}_p^{n+1}/({\mathbb {F}}_p v)$
induced by
${\mathbb {F}}_p^{n+1}/({\mathbb {F}}_p v)$
induced by
![]() $B_0$
. The determinant
$B_0$
. The determinant
![]() $1$
condition then gives
$1$
condition then gives
Finally, since
![]() $\#J_{xf}[2]({\mathbb {F}}_p)\ll _n 1$
, we have
$\#J_{xf}[2]({\mathbb {F}}_p)\ll _n 1$
, we have
as desired.
Corollary 6.8. Fix
![]() $a\in {\mathbb {F}}_p^\times $
and
$a\in {\mathbb {F}}_p^\times $
and
![]() $B_0\in S({\mathbb {F}}_p)$
with rank n. Let
$B_0\in S({\mathbb {F}}_p)$
with rank n. Let
![]() $S_{B_0}^{\mathrm {{ndist}}}({\mathbb {F}}_p)_{a_{11}=a}$
denote the set of all elements
$S_{B_0}^{\mathrm {{ndist}}}({\mathbb {F}}_p)_{a_{11}=a}$
denote the set of all elements
![]() $A\in S_{B_0}^{\mathrm {{ndist}}}({\mathbb {F}}_p)$
with
$A\in S_{B_0}^{\mathrm {{ndist}}}({\mathbb {F}}_p)$
with
![]() $a_{11}=a$
. Then
$a_{11}=a$
. Then
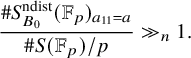 $$ \begin{align*} \frac{\#S_{B_0}^{\mathrm{{ndist}}}({\mathbb{F}}_p)_{a_{11}=a}}{\#S({\mathbb{F}}_p)/p}\gg_n 1. \end{align*} $$
$$ \begin{align*} \frac{\#S_{B_0}^{\mathrm{{ndist}}}({\mathbb{F}}_p)_{a_{11}=a}}{\#S({\mathbb{F}}_p)/p}\gg_n 1. \end{align*} $$
Proof. Since the property of
![]() $(A,B_0)$
being nondistinguished is preserved when A is multiplied by an element of
$(A,B_0)$
being nondistinguished is preserved when A is multiplied by an element of
![]() ${\mathbb {F}}_p^\times $
, the claim follows immediately from Lemma 6.7.
${\mathbb {F}}_p^\times $
, the claim follows immediately from Lemma 6.7.
We now bound the number of pairs
![]() $(A,B)$
in the main body where the first row and column of B are zero.
$(A,B)$
in the main body where the first row and column of B are zero.
Proposition 6.9. We have
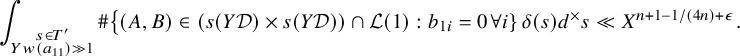 $$ \begin{align} \int_{\substack{s\in T'\\Yw(a_{11})\gg 1}}\#\big\{(A,B)\in (s(Y{\mathcal{D}})\times s(Y{\mathcal{D}}))\cap {{\mathcal{L}}(1)} : b_{1i}=0\,\forall i\} \,\delta(s)d^\times s \ll X^{n+1-1/(4n)+\epsilon}. \end{align} $$
$$ \begin{align} \int_{\substack{s\in T'\\Yw(a_{11})\gg 1}}\#\big\{(A,B)\in (s(Y{\mathcal{D}})\times s(Y{\mathcal{D}}))\cap {{\mathcal{L}}(1)} : b_{1i}=0\,\forall i\} \,\delta(s)d^\times s \ll X^{n+1-1/(4n)+\epsilon}. \end{align} $$
Proof. Let
![]() $s\in T'$
be an element with
$s\in T'$
be an element with
![]() $Yw(a_{11})\gg 1$
. Then
$Yw(a_{11})\gg 1$
. Then
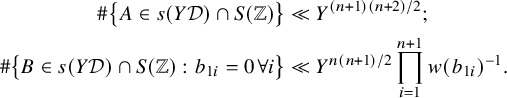 $$ \begin{align*} \#\big\{A\in s(Y{\mathcal{D}})\cap S({\mathbb{Z}})\big\}&\ll Y^{(n+1)(n+2)/2}; \\ \#\big\{B\in s(Y{\mathcal{D}})\cap S({\mathbb{Z}}):b_{1i}=0\,\forall i\big\} &\ll Y^{n(n+1)/2}\prod_{i=1}^{n+1}w(b_{1i})^{-1}. \end{align*} $$
$$ \begin{align*} \#\big\{A\in s(Y{\mathcal{D}})\cap S({\mathbb{Z}})\big\}&\ll Y^{(n+1)(n+2)/2}; \\ \#\big\{B\in s(Y{\mathcal{D}})\cap S({\mathbb{Z}}):b_{1i}=0\,\forall i\big\} &\ll Y^{n(n+1)/2}\prod_{i=1}^{n+1}w(b_{1i})^{-1}. \end{align*} $$
For each
![]() $B\in s(Y{\mathcal {D}})\cap S({\mathbb {Z}})$
having rank n, we bound the number of
$B\in s(Y{\mathcal {D}})\cap S({\mathbb {Z}})$
having rank n, we bound the number of
![]() $A\in s(Y{\mathcal {D}})\cap S({\mathbb {Z}})$
such that
$A\in s(Y{\mathcal {D}})\cap S({\mathbb {Z}})$
such that
![]() $(A,B)$
is distinguished. Indeed, after additionally fibering over the coefficient
$(A,B)$
is distinguished. Indeed, after additionally fibering over the coefficient
![]() $a_{11}$
, Corollary 6.8 in conjunction with an application of the large sieve in Proposition 4.3, we obtain a saving of
$a_{11}$
, Corollary 6.8 in conjunction with an application of the large sieve in Proposition 4.3, we obtain a saving of
![]() $(Yw(a_{12}))^{-1/2+\epsilon }$
.
$(Yw(a_{12}))^{-1/2+\epsilon }$
.
Therefore, the left-hand side of (45) is
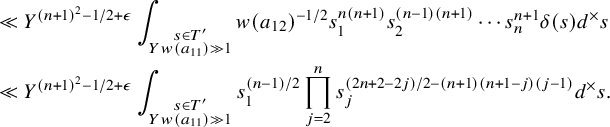 $$ \begin{align} \begin{aligned} &\ll Y^{(n+1)^2-1/2+\epsilon}\int_{\substack{s\in T'\\Yw(a_{11})\gg 1}} w(a_{12})^{-1/2}s_1^{n(n+1)}s_2^{(n-1)(n+1)}\cdots s_n^{n+1} \delta(s)d^\times s \\ &\ll Y^{(n+1)^2-1/2+\epsilon}\int_{\substack{s\in T'\\Yw(a_{11})\gg 1}} s_1^{(n-1)/2}\prod_{j=2}^{n}s_j^{(2n+2-2j)/2-(n+1)(n+1-j)(j-1)}d^\times s. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\ll Y^{(n+1)^2-1/2+\epsilon}\int_{\substack{s\in T'\\Yw(a_{11})\gg 1}} w(a_{12})^{-1/2}s_1^{n(n+1)}s_2^{(n-1)(n+1)}\cdots s_n^{n+1} \delta(s)d^\times s \\ &\ll Y^{(n+1)^2-1/2+\epsilon}\int_{\substack{s\in T'\\Yw(a_{11})\gg 1}} s_1^{(n-1)/2}\prod_{j=2}^{n}s_j^{(2n+2-2j)/2-(n+1)(n+1-j)(j-1)}d^\times s. \end{aligned} \end{align} $$
In particular, the power of
![]() $s_i$
above is negative for all
$s_i$
above is negative for all
![]() $j\in \{2,\ldots ,n\}$
, and hence, the integral over
$j\in \{2,\ldots ,n\}$
, and hence, the integral over
![]() $s_2,\ldots ,s_n$
is absolutely bounded. The condition that
$s_2,\ldots ,s_n$
is absolutely bounded. The condition that
![]() $Yw(a_{11})\gg 1$
on the integrand implies that we have
$Yw(a_{11})\gg 1$
on the integrand implies that we have
![]() $s_1\ll Y^{1/(2n)}$
. Therefore, the terms in (46) are
$s_1\ll Y^{1/(2n)}$
. Therefore, the terms in (46) are
Since
![]() $Y=X^{1/(n+1)}$
, we obtain the result.
$Y=X^{1/(n+1)}$
, we obtain the result.
Remark 6.10. Our use of the large sieve saves a power of the smallest range of any coordinate. In the above proof, we fiber over
![]() $a_{11}$
because in the region of the main body close to the cusp, just before we enter the shallow cusp, the range of
$a_{11}$
because in the region of the main body close to the cusp, just before we enter the shallow cusp, the range of
![]() $a_{11}$
has size
$a_{11}$
has size
![]() $\ll 1$
. In this case, the large sieve gives no saving at all. Once we fiber over
$\ll 1$
. In this case, the large sieve gives no saving at all. Once we fiber over
![]() $a_{11}$
, the next smallest range is that of
$a_{11}$
, the next smallest range is that of
![]() $a_{12}$
. Implicit in our proof is an argument that either the range of
$a_{12}$
. Implicit in our proof is an argument that either the range of
![]() $a_{12}$
is large, in which case the large sieve gives the desired saving, or the number of pairs
$a_{12}$
is large, in which case the large sieve gives the desired saving, or the number of pairs
![]() $(A,B)$
is automatically small.
$(A,B)$
is automatically small.
Proof of Theorem 6.6.
Recall from (40) that we have
where the second sum is over all saturated
![]() ${\mathcal {Z}}$
. Since
${\mathcal {Z}}$
. Since
![]() ${\mathcal {Z}}$
is saturated and
${\mathcal {Z}}$
is saturated and
![]() $a_{11}\not \in {\mathcal {Z}}$
, we have
$a_{11}\not \in {\mathcal {Z}}$
, we have
![]() ${\mathcal {Z}}\subset {\mathcal {M}}$
. If
${\mathcal {Z}}\subset {\mathcal {M}}$
. If
![]() $\ell _{k,1}=0$
for every
$\ell _{k,1}=0$
for every
![]() $k=1,\ldots ,n$
, then
$k=1,\ldots ,n$
, then
![]() $(1,0,\ldots ,0)$
is in the kernel of B implying that the top row of B is zero. The number of such pairs
$(1,0,\ldots ,0)$
is in the kernel of B implying that the top row of B is zero. The number of such pairs
![]() $(A,B)$
has already been bounded in Proposition 6.9, and hence, we may assume that
$(A,B)$
has already been bounded in Proposition 6.9, and hence, we may assume that
![]() $\ell _{n,1}\not \in {\mathcal {Z}}$
. Fix a nondecreasing n-tuple L of positive real numbers, and a saturated
$\ell _{n,1}\not \in {\mathcal {Z}}$
. Fix a nondecreasing n-tuple L of positive real numbers, and a saturated
![]() ${\mathcal {Z}}\subset {\mathcal {M}}$
with
${\mathcal {Z}}\subset {\mathcal {M}}$
with
![]() $\ell _{n,1}\not \in {\mathcal {Z}}$
such that
$\ell _{n,1}\not \in {\mathcal {Z}}$
such that
![]() $N({{\mathcal {L}}(1)} ,L,{\mathcal {Z}},X)\neq 0$
. We partition the integrand
$N({{\mathcal {L}}(1)} ,L,{\mathcal {Z}},X)\neq 0$
. We partition the integrand
![]() $T_{\mathcal {Z}}(L,Y)$
into two parts: let
$T_{\mathcal {Z}}(L,Y)$
into two parts: let
![]() $T_1$
denote the subset of
$T_1$
denote the subset of
![]() $T_{\mathcal {Z}}(L,Y)$
consisting of elements s for
$T_{\mathcal {Z}}(L,Y)$
consisting of elements s for
![]() $s=(s_i)_i$
with
$s=(s_i)_i$
with
![]() $s_n\geq Y^\delta $
, and let
$s_n\geq Y^\delta $
, and let
![]() $T_2$
denote the subset of elements s with
$T_2$
denote the subset of elements s with
![]() $1\ll s_n< Y^\delta $
, where
$1\ll s_n< Y^\delta $
, where
![]() $\delta $
is a positive constant to be optimized later.
$\delta $
is a positive constant to be optimized later.
We first bound the contribution to
![]() $N({{\mathcal {L}}(1)} ,L,{\mathcal {Z}},X)$
from
$N({{\mathcal {L}}(1)} ,L,{\mathcal {Z}},X)$
from
![]() $T_1$
. Since
$T_1$
. Since
![]() $Yw(a_{11})\gg 1$
, we have
$Yw(a_{11})\gg 1$
, we have
for
![]() $s\in T_1$
. Integrating over
$s\in T_1$
. Integrating over
![]() $T_1$
gives the bound
$T_1$
gives the bound
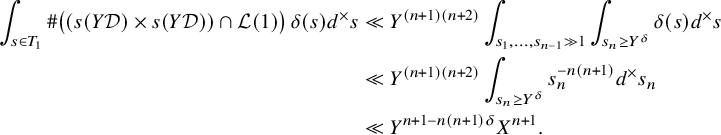 $$ \begin{align} \begin{aligned} \int_{s\in T_1} \#\big((s(Y{\mathcal{D}})\times s(Y{\mathcal{D}}))\cap {{\mathcal{L}}(1)} \big)\,\delta(s)d^\times s&\ll Y^{(n+1)(n+2)}\int_{s_1,\ldots,s_{n-1}\gg 1} \int_{s_n\geq Y^{\delta}}\delta(s)d^\times s \\ &\ll Y^{(n+1)(n+2)}\int_{s_n\geq Y^{\delta}}s_n^{-n(n+1)}d^\times s_n \\ &\ll Y^{n+1-n(n+1)\delta}X^{n+1}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \int_{s\in T_1} \#\big((s(Y{\mathcal{D}})\times s(Y{\mathcal{D}}))\cap {{\mathcal{L}}(1)} \big)\,\delta(s)d^\times s&\ll Y^{(n+1)(n+2)}\int_{s_1,\ldots,s_{n-1}\gg 1} \int_{s_n\geq Y^{\delta}}\delta(s)d^\times s \\ &\ll Y^{(n+1)(n+2)}\int_{s_n\geq Y^{\delta}}s_n^{-n(n+1)}d^\times s_n \\ &\ll Y^{n+1-n(n+1)\delta}X^{n+1}. \end{aligned} \end{align} $$
Next, we consider the contribution from
![]() $T_2$
. Define the map
$T_2$
. Define the map
![]() $\pi :{\mathcal {Z}}_1\cap {\mathcal {M}}\to {\mathcal {M}}$
by
$\pi :{\mathcal {Z}}_1\cap {\mathcal {M}}\to {\mathcal {M}}$
by
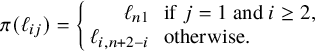 $$ \begin{align*} \pi(\ell_{ij}) = \left\{ \begin{array}{rl} \ell_{n1}&\;\mathrm{if}\; j=1\text{ and }i\geq 2,\\ \ell_{i,n+2-i} &\;\mathrm{otherwise}. \end{array}\right. \end{align*} $$
$$ \begin{align*} \pi(\ell_{ij}) = \left\{ \begin{array}{rl} \ell_{n1}&\;\mathrm{if}\; j=1\text{ and }i\geq 2,\\ \ell_{i,n+2-i} &\;\mathrm{otherwise}. \end{array}\right. \end{align*} $$
Since we have assumed that
![]() $N({{\mathcal {L}}(1)} ,L,{\mathcal {Z}},X)\neq 0$
, Lemma 6.5 implies that
$N({{\mathcal {L}}(1)} ,L,{\mathcal {Z}},X)\neq 0$
, Lemma 6.5 implies that
![]() ${\mathcal {Z}}\subset {\mathcal {Z}}_1$
, and so the image of
${\mathcal {Z}}\subset {\mathcal {Z}}_1$
, and so the image of
![]() $\pi $
lies in
$\pi $
lies in
![]() ${\mathcal {M}}\backslash {\mathcal {Z}}$
. Then for any
${\mathcal {M}}\backslash {\mathcal {Z}}$
. Then for any
![]() $\alpha \in {\mathcal {Z}}_1\cap {\mathcal {M}}$
and any
$\alpha \in {\mathcal {Z}}_1\cap {\mathcal {M}}$
and any
![]() $s\in T_{\mathcal {Z}}(L,Y)$
, we have
$s\in T_{\mathcal {Z}}(L,Y)$
, we have
![]() $w_L(\pi (\alpha ))\gg w_L(\alpha )$
and
$w_L(\pi (\alpha ))\gg w_L(\alpha )$
and
![]() $w_L(\pi (\alpha ))\gg 1$
. These inequalities along with (43) and (44) imply that for any
$w_L(\pi (\alpha ))\gg 1$
. These inequalities along with (43) and (44) imply that for any
![]() $s\in T_{\mathcal {Z}}(L,Y)$
, the number
$s\in T_{\mathcal {Z}}(L,Y)$
, the number
![]() $\# (s(Y{\mathcal {D}}) \cap {\mathcal {S}}(L,s))$
of possible B’s is
$\# (s(Y{\mathcal {D}}) \cap {\mathcal {S}}(L,s))$
of possible B’s is
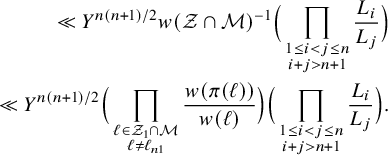 $$ \begin{align*} \ll Y^{n(n+1)/2}w({\mathcal{Z}}\cap{\mathcal{M}})^{-1}\Big(\prod_{\substack{1\leq i< j\leq n\\i+j>n+1}} \frac{L_i}{L_j}\Big)\\ \ll Y^{n(n+1)/2}\Big(\prod_{\substack{\ell\in {\mathcal{Z}}_1\cap{\mathcal{M}}\\\ell\neq \ell_{n1}}} \frac{w(\pi(\ell))}{w(\ell)}\Big) \Big(\prod_{\substack{1\leq i< j\leq n\\i+j>n+1}} \frac{L_i}{L_j}\Big). \end{align*} $$
$$ \begin{align*} \ll Y^{n(n+1)/2}w({\mathcal{Z}}\cap{\mathcal{M}})^{-1}\Big(\prod_{\substack{1\leq i< j\leq n\\i+j>n+1}} \frac{L_i}{L_j}\Big)\\ \ll Y^{n(n+1)/2}\Big(\prod_{\substack{\ell\in {\mathcal{Z}}_1\cap{\mathcal{M}}\\\ell\neq \ell_{n1}}} \frac{w(\pi(\ell))}{w(\ell)}\Big) \Big(\prod_{\substack{1\leq i< j\leq n\\i+j>n+1}} \frac{L_i}{L_j}\Big). \end{align*} $$
For each possible B, applying the large sieve (Proposition 4.3) using Lemma 6.7 gives us a bound of
for the number of possible choices for A. Therefore,
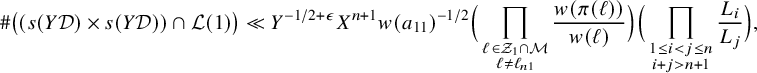 $$ \begin{align*} \#\big((s(Y{\mathcal{D}})\times s(Y{\mathcal{D}}))\cap {{\mathcal{L}}(1)} \big) \ll Y^{-1/2+\epsilon}X^{n+1}w(a_{11})^{-1/2} \Big(\prod_{\substack{\ell\in {\mathcal{Z}}_1\cap{\mathcal{M}}\\\ell\neq \ell_{n1}}} \frac{w(\pi(\ell))}{w(\ell)}\Big) \Big(\prod_{\substack{1\leq i < j\leq n\\i+j>n+1}} \frac{L_i}{L_j}\Big), \end{align*} $$
$$ \begin{align*} \#\big((s(Y{\mathcal{D}})\times s(Y{\mathcal{D}}))\cap {{\mathcal{L}}(1)} \big) \ll Y^{-1/2+\epsilon}X^{n+1}w(a_{11})^{-1/2} \Big(\prod_{\substack{\ell\in {\mathcal{Z}}_1\cap{\mathcal{M}}\\\ell\neq \ell_{n1}}} \frac{w(\pi(\ell))}{w(\ell)}\Big) \Big(\prod_{\substack{1\leq i < j\leq n\\i+j>n+1}} \frac{L_i}{L_j}\Big), \end{align*} $$
for
![]() $s\in T_2$
. We compute the ratio of these weights: For any
$s\in T_2$
. We compute the ratio of these weights: For any
![]() $i\geq 2$
and
$i\geq 2$
and
![]() $j=1$
, we have
$j=1$
, we have
For any other
![]() $i,j$
, we have
$i,j$
, we have
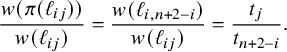 $$ \begin{align*} \frac{w(\pi(\ell_{ij}))}{w(\ell_{ij})}=\frac{w(\ell_{i,n+2-i})}{w(\ell_{ij})} =\frac{t_j}{t_{n+2-i}}. \end{align*} $$
$$ \begin{align*} \frac{w(\pi(\ell_{ij}))}{w(\ell_{ij})}=\frac{w(\ell_{i,n+2-i})}{w(\ell_{ij})} =\frac{t_j}{t_{n+2-i}}. \end{align*} $$
As the
![]() $L_i$
are nondecreasing and positive, we multiply by the Haar measure character
$L_i$
are nondecreasing and positive, we multiply by the Haar measure character
![]() $\delta (s)$
to obtain
$\delta (s)$
to obtain
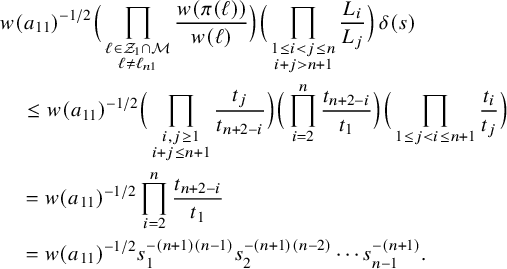 $$ \begin{align*} \begin{aligned} & w(a_{11})^{-1/2}\Big(\prod_{\substack{\ell\in {\mathcal{Z}}_1\cap{\mathcal{M}}\\\ell\neq \ell_{n1}}} \frac{w(\pi(\ell))}{w(\ell)}\Big) \Big(\prod_{\substack{1\leq i < j\leq n\\i+j>n+1}} \frac{L_i}{L_j}\Big)\,\delta(s)\\ &\quad \leq w(a_{11})^{-1/2} \Big(\prod_{\substack{i,j\geq 1\\i+j\leq n+1}}\frac{t_j}{t_{n+2-i}}\Big)\Big( \prod_{i=2}^{n}\frac{t_{n+2-i}}{t_1}\Big) \Big(\prod_{1\leq j < i \leq n+1}\frac{t_i}{t_j}\Big) \\ &\quad = w(a_{11})^{-1/2} \prod_{i=2}^{n}\frac{t_{n+2-i}}{t_1} \\ &\quad = w(a_{11})^{-1/2}s_1^{-(n+1)(n-1)}s_2^{-(n+1)(n-2)}\cdots s_{n-1}^{-(n+1)}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} & w(a_{11})^{-1/2}\Big(\prod_{\substack{\ell\in {\mathcal{Z}}_1\cap{\mathcal{M}}\\\ell\neq \ell_{n1}}} \frac{w(\pi(\ell))}{w(\ell)}\Big) \Big(\prod_{\substack{1\leq i < j\leq n\\i+j>n+1}} \frac{L_i}{L_j}\Big)\,\delta(s)\\ &\quad \leq w(a_{11})^{-1/2} \Big(\prod_{\substack{i,j\geq 1\\i+j\leq n+1}}\frac{t_j}{t_{n+2-i}}\Big)\Big( \prod_{i=2}^{n}\frac{t_{n+2-i}}{t_1}\Big) \Big(\prod_{1\leq j < i \leq n+1}\frac{t_i}{t_j}\Big) \\ &\quad = w(a_{11})^{-1/2} \prod_{i=2}^{n}\frac{t_{n+2-i}}{t_1} \\ &\quad = w(a_{11})^{-1/2}s_1^{-(n+1)(n-1)}s_2^{-(n+1)(n-2)}\cdots s_{n-1}^{-(n+1)}. \end{aligned} \end{align*} $$
The powers of
![]() $s_i$
in the above expression are negative for
$s_i$
in the above expression are negative for
![]() $1\leq i\leq n-1$
, while the power of
$1\leq i\leq n-1$
, while the power of
![]() $s_n$
is
$s_n$
is
![]() $1$
. Integrating over
$1$
. Integrating over
![]() $T_2$
now gives the bound
$T_2$
now gives the bound
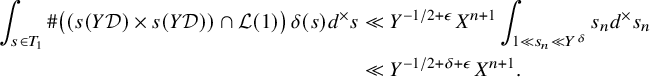 $$ \begin{align} \begin{aligned}\int_{s\in T_1} \#\big((s(Y{\mathcal{D}})\times s(Y{\mathcal{D}}))\cap {{\mathcal{L}}(1)} \big)\,\delta(s)d^\times s&\ll Y^{-1/2+\epsilon}X^{n+1}\int_{1\ll s_n\ll Y^\delta}s_nd^\times s_n \\ &\ll Y^{-1/2+\delta+\epsilon}X^{n+1}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned}\int_{s\in T_1} \#\big((s(Y{\mathcal{D}})\times s(Y{\mathcal{D}}))\cap {{\mathcal{L}}(1)} \big)\,\delta(s)d^\times s&\ll Y^{-1/2+\epsilon}X^{n+1}\int_{1\ll s_n\ll Y^\delta}s_nd^\times s_n \\ &\ll Y^{-1/2+\delta+\epsilon}X^{n+1}. \end{aligned} \end{align} $$
Combining (47) and (48) and choosing
![]() $\delta =\frac {n+3/2}{n^2 + n + 1}$
yields
$\delta =\frac {n+3/2}{n^2 + n + 1}$
yields
The summation of this bound over the
![]() $O(1)$
different possible
$O(1)$
different possible
![]() ${\mathcal {Z}}$
’s and the
${\mathcal {Z}}$
’s and the
![]() $O(Y^\epsilon )$
different possible L’s, in conjunction with the bound in Proposition 6.9, implies Theorem 6.6.
$O(Y^\epsilon )$
different possible L’s, in conjunction with the bound in Proposition 6.9, implies Theorem 6.6.
6.3 Bounding the number of distinguished elements in the shallow cusp
In this subsection, we bound the number of distinguished elements having large q-invariant that lie in the shallow cusp of the fundamental domain.
Theorem 6.11. Let
![]() $\eta>0$
be any real number. Assume that
$\eta>0$
be any real number. Assume that
![]() $M>X^{\eta }$
. Then
$M>X^{\eta }$
. Then
We will take
![]() $\eta = 1/4$
when we prove Theorem 5 in §6.5.
$\eta = 1/4$
when we prove Theorem 5 in §6.5.
6.3.1 A preliminary bound of
 $O_\epsilon (X^{n+1+\epsilon })$
$O_\epsilon (X^{n+1+\epsilon })$
We again use (40) to write
where the sum is over nondecreasing n-tuples
![]() $L=(L_1,\ldots ,L_n)$
of positive real numbers that partition the region
$L=(L_1,\ldots ,L_n)$
of positive real numbers that partition the region
![]() $\{(\mu _1,\ldots ,\mu _n)\in [Y^{-\Theta _1},Y^{\Theta _2}]^n:\mu _1\leq \mu _2\leq \ldots \leq \mu _n\}$
into dyadic ranges, and over saturated
$\{(\mu _1,\ldots ,\mu _n)\in [Y^{-\Theta _1},Y^{\Theta _2}]^n:\mu _1\leq \mu _2\leq \ldots \leq \mu _n\}$
into dyadic ranges, and over saturated
![]() ${\mathcal {Z}}\subset {\mathcal {K}}\cup {\mathcal {M}}$
such that
${\mathcal {Z}}\subset {\mathcal {K}}\cup {\mathcal {M}}$
such that
![]() $a_{11}\in {\mathcal {Z}}$
and
$a_{11}\in {\mathcal {Z}}$
and
![]() $a_{g+1,g+1}\not \in {\mathcal {Z}}$
. By Lemma 6.5, we have
$a_{g+1,g+1}\not \in {\mathcal {Z}}$
. By Lemma 6.5, we have
![]() $N({{\mathcal {L}}(M)} ,L,{\mathcal {Z}},X)>0$
only when
$N({{\mathcal {L}}(M)} ,L,{\mathcal {Z}},X)>0$
only when
![]() ${\mathcal {Z}}\subset {\mathcal {Z}}_1$
, which we henceforth assume.
${\mathcal {Z}}\subset {\mathcal {Z}}_1$
, which we henceforth assume.
For
![]() $k\in \{0,\ldots ,g\}$
, define the map
$k\in \{0,\ldots ,g\}$
, define the map
![]() $\pi _k:{\mathcal {Z}}_1\to {\mathcal {K}}\cup {\mathcal {M}}$
by
$\pi _k:{\mathcal {Z}}_1\to {\mathcal {K}}\cup {\mathcal {M}}$
by
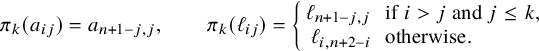 $$ \begin{align*} \pi_k(a_{ij}) = a_{n+1-j,j},\qquad \pi_k(\ell_{ij}) = \left\{ \begin{array}{rl} \ell_{n+1-j,j}&\;\mathrm{if}\; i>j\text{ and }j\leq k,\\ \ell_{i,n+2-i} &\;\mathrm{otherwise}. \end{array}\right. \end{align*} $$
$$ \begin{align*} \pi_k(a_{ij}) = a_{n+1-j,j},\qquad \pi_k(\ell_{ij}) = \left\{ \begin{array}{rl} \ell_{n+1-j,j}&\;\mathrm{if}\; i>j\text{ and }j\leq k,\\ \ell_{i,n+2-i} &\;\mathrm{otherwise}. \end{array}\right. \end{align*} $$
We define the auxiliary set
![]() ${\mathcal {Z}}^*$
by
${\mathcal {Z}}^*$
by
Then, when restricted to
![]() ${\mathcal {Z}}^*\subset {\mathcal {Z}}_1$
, the functions
${\mathcal {Z}}^*\subset {\mathcal {Z}}_1$
, the functions
![]() $\pi _k$
are equal for every k.
$\pi _k$
are equal for every k.
Lemma 6.12. For any
![]() $k\in \{0,\ldots ,g\}$
, we have
$k\in \{0,\ldots ,g\}$
, we have
 $$ \begin{align} \Big(\prod_{\alpha\in {\mathcal{Z}}^*} \frac{w(\pi_k(\alpha))}{w(\alpha)} \Big)\,\delta(s)=1. \end{align} $$
$$ \begin{align} \Big(\prod_{\alpha\in {\mathcal{Z}}^*} \frac{w(\pi_k(\alpha))}{w(\alpha)} \Big)\,\delta(s)=1. \end{align} $$
Proof. We directly compute
 $$ \begin{align*} \begin{aligned}\prod_{\alpha\in {\mathcal{Z}}^*} \frac{w(\pi_k(\alpha))}{w(\alpha)} &= \Big(\prod_{\substack{i\leq j\\i+j<n+1}}\frac{w(a_{n+1-j,j})}{w(a_{ij})}\Big) \Big(\prod_{\substack{i\leq j\\i+j<n+2}}\frac{w(\ell_{i,n+2-i})}{w(\ell_{ij})}\Big) \\ &= \Big(\prod_{\substack{i\leq j\\i+j<n+1}}\frac{t_i}{t_{n+1-j}}\Big) \Big(\prod_{\substack{i\leq j\\i+j<n+2}}\frac{t_j}{t_{n+2-i}}\Big) \\ &= \Big(\prod_{\substack{i<r\\i+r\leq n+1}}\frac{t_i}{t_{r}}\Big) \Big(\prod_{\substack{j< r\\j+r\geq n+2}}\frac{t_j}{t_{r}}\Big), \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned}\prod_{\alpha\in {\mathcal{Z}}^*} \frac{w(\pi_k(\alpha))}{w(\alpha)} &= \Big(\prod_{\substack{i\leq j\\i+j<n+1}}\frac{w(a_{n+1-j,j})}{w(a_{ij})}\Big) \Big(\prod_{\substack{i\leq j\\i+j<n+2}}\frac{w(\ell_{i,n+2-i})}{w(\ell_{ij})}\Big) \\ &= \Big(\prod_{\substack{i\leq j\\i+j<n+1}}\frac{t_i}{t_{n+1-j}}\Big) \Big(\prod_{\substack{i\leq j\\i+j<n+2}}\frac{t_j}{t_{n+2-i}}\Big) \\ &= \Big(\prod_{\substack{i<r\\i+r\leq n+1}}\frac{t_i}{t_{r}}\Big) \Big(\prod_{\substack{j< r\\j+r\geq n+2}}\frac{t_j}{t_{r}}\Big), \end{aligned} \end{align*} $$
which is
![]() $\delta (s)^{-1}$
.
$\delta (s)^{-1}$
.
Fix a saturated set
![]() ${\mathcal {Z}}\subset {\mathcal {Z}}_1$
such that
${\mathcal {Z}}\subset {\mathcal {Z}}_1$
such that
![]() $a_{11}\in {\mathcal {Z}}$
,
$a_{11}\in {\mathcal {Z}}$
,
![]() $a_{g+1,g+1}\notin {\mathcal {Z}}$
and
$a_{g+1,g+1}\notin {\mathcal {Z}}$
and
![]() $N({{\mathcal {L}}(M)} ,L,{\mathcal {Z}},X)>0$
. Let
$N({{\mathcal {L}}(M)} ,L,{\mathcal {Z}},X)>0$
. Let
![]() $k\in \{1,\ldots ,g\}$
be the largest integer such that
$k\in \{1,\ldots ,g\}$
be the largest integer such that
![]() $a_{kk}\in {\mathcal {Z}}$
. Then we have the following results.
$a_{kk}\in {\mathcal {Z}}$
. Then we have the following results.
Lemma 6.13. Let
![]() ${\mathcal {Z}}$
and k be as above. Then for every
${\mathcal {Z}}$
and k be as above. Then for every
![]() $\alpha \in {\mathcal {Z}}$
, we have
$\alpha \in {\mathcal {Z}}$
, we have
![]() $\pi _k(\alpha )\notin {\mathcal {Z}}$
. In particular, for any
$\pi _k(\alpha )\notin {\mathcal {Z}}$
. In particular, for any
![]() $s\in T_{\mathcal {Z}}(L,Y)$
, we have
$s\in T_{\mathcal {Z}}(L,Y)$
, we have
![]() $Yw(\pi _k(\alpha ))\gg 1.$
$Yw(\pi _k(\alpha ))\gg 1.$
Proof. Since
![]() $a_{n+1-j,j}\not \in {\mathcal {Z}}_1$
for any j and
$a_{n+1-j,j}\not \in {\mathcal {Z}}_1$
for any j and
![]() ${\mathcal {Z}}\subset {\mathcal {Z}}_1$
, we have
${\mathcal {Z}}\subset {\mathcal {Z}}_1$
, we have
![]() $\pi _k(a_{ij})\not \in {\mathcal {Z}}$
for any
$\pi _k(a_{ij})\not \in {\mathcal {Z}}$
for any
![]() $a_{ij}\in {\mathcal {Z}}$
. Moreover, since
$a_{ij}\in {\mathcal {Z}}$
. Moreover, since
![]() $a_{jj}\in {\mathcal {Z}}$
for every
$a_{jj}\in {\mathcal {Z}}$
for every
![]() $j\leq k$
, it follows from Lemma 6.5 that
$j\leq k$
, it follows from Lemma 6.5 that
![]() $\ell _{n+1-j,j}\not \in {\mathcal {Z}}$
. Furthermore,
$\ell _{n+1-j,j}\not \in {\mathcal {Z}}$
. Furthermore,
![]() $\ell _{i,n+2-i}\not \in {\mathcal {Z}}_1$
. Hence,
$\ell _{i,n+2-i}\not \in {\mathcal {Z}}_1$
. Hence,
![]() $\pi _k(\ell _{ij})\not \in {\mathcal {Z}}$
for any
$\pi _k(\ell _{ij})\not \in {\mathcal {Z}}$
for any
![]() $\ell _{ij}\in {\mathcal {Z}}$
.
$\ell _{ij}\in {\mathcal {Z}}$
.
Lemma 6.14. Let
![]() ${\mathcal {Z}}$
and k be as above. Then, uniformly for
${\mathcal {Z}}$
and k be as above. Then, uniformly for
![]() $s\in T_{\mathcal {Z}}(L,Y)$
, we have
$s\in T_{\mathcal {Z}}(L,Y)$
, we have
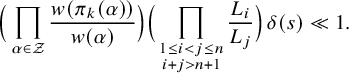 $$ \begin{align} \Big(\prod_{\alpha\in {\mathcal{Z}}} \frac{w(\pi_k(\alpha))}{w(\alpha)}\Big) \Big(\prod_{\substack{1\leq i < j\leq n\\ i+j> n+1}}\frac{L_i}{L_j}\Big) \,\delta(s) \ll 1. \end{align} $$
$$ \begin{align} \Big(\prod_{\alpha\in {\mathcal{Z}}} \frac{w(\pi_k(\alpha))}{w(\alpha)}\Big) \Big(\prod_{\substack{1\leq i < j\leq n\\ i+j> n+1}}\frac{L_i}{L_j}\Big) \,\delta(s) \ll 1. \end{align} $$
Proof. Since we have
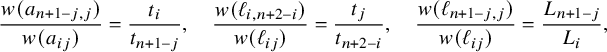 $$ \begin{align*} \frac{w(a_{n+1-j,j})}{w(a_{ij})}=\frac{t_i}{t_{n+1-j}},\quad \frac{w(\ell_{i,n+2-i})}{w(\ell_{ij})}=\frac{t_j}{t_{n+2-i}},\quad \frac{w(\ell_{n+1-j,j})}{w(\ell_{ij})}=\frac{L_{n+1-j}}{L_i}, \end{align*} $$
$$ \begin{align*} \frac{w(a_{n+1-j,j})}{w(a_{ij})}=\frac{t_i}{t_{n+1-j}},\quad \frac{w(\ell_{i,n+2-i})}{w(\ell_{ij})}=\frac{t_j}{t_{n+2-i}},\quad \frac{w(\ell_{n+1-j,j})}{w(\ell_{ij})}=\frac{L_{n+1-j}}{L_i}, \end{align*} $$
it follows that
![]() $w(\pi _k(\alpha ))/w(\alpha )\gg 1$
for every k,
$w(\pi _k(\alpha ))/w(\alpha )\gg 1$
for every k,
![]() $\alpha \in {\mathcal {Z}}_1$
, and
$\alpha \in {\mathcal {Z}}_1$
, and
![]() $s\in T_{\mathcal {Z}}(L,Y)$
. Thus, by adding elements in
$s\in T_{\mathcal {Z}}(L,Y)$
. Thus, by adding elements in
![]() ${\mathcal {Z}}_1$
to
${\mathcal {Z}}_1$
to
![]() ${\mathcal {Z}}$
, if necessary, we can assume that
${\mathcal {Z}}$
, if necessary, we can assume that
![]() ${\mathcal {Z}}$
is equal to
${\mathcal {Z}}$
is equal to
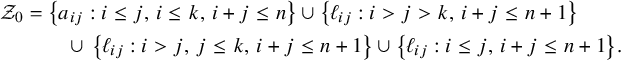 $$ \begin{align*} \begin{aligned} {\mathcal{Z}}_0&=\big\{a_{ij}:i\leq j,\,i\leq k,\,i+j\leq n\big\}\cup \big\{\ell_{ij}:i>j> k,\,i+j\leq n+1\big\} \\ &\qquad \cup\,\big\{\ell_{ij}:i>j,\,j\leq k,\,i+j\leq n+1\big\} \cup\big\{\ell_{ij}:i\leq j,\,i+j\leq n+1\big\}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} {\mathcal{Z}}_0&=\big\{a_{ij}:i\leq j,\,i\leq k,\,i+j\leq n\big\}\cup \big\{\ell_{ij}:i>j> k,\,i+j\leq n+1\big\} \\ &\qquad \cup\,\big\{\ell_{ij}:i>j,\,j\leq k,\,i+j\leq n+1\big\} \cup\big\{\ell_{ij}:i\leq j,\,i+j\leq n+1\big\}. \end{aligned} \end{align*} $$
Denote the four sets on the right-hand side of the above equation as
![]() $S_1$
,
$S_1$
,
![]() $S_2$
,
$S_2$
,
![]() $S_3$
and
$S_3$
and
![]() $S_4$
, respectively. For an element
$S_4$
, respectively. For an element
![]() $\ell _{ij}\in S_2$
, we have
$\ell _{ij}\in S_2$
, we have
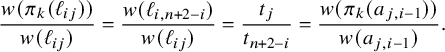 $$ \begin{align*} \frac{w(\pi_k(\ell_{ij}))}{w(\ell_{ij})}=\frac{w(\ell_{i,n+2-i})}{w(\ell_{ij})} =\frac{t_j}{t_{n+2-i}}=\frac{w(\pi_k(a_{j,i-1}))}{w(a_{j,i-1})}. \end{align*} $$
$$ \begin{align*} \frac{w(\pi_k(\ell_{ij}))}{w(\ell_{ij})}=\frac{w(\ell_{i,n+2-i})}{w(\ell_{ij})} =\frac{t_j}{t_{n+2-i}}=\frac{w(\pi_k(a_{j,i-1}))}{w(a_{j,i-1})}. \end{align*} $$
Therefore,
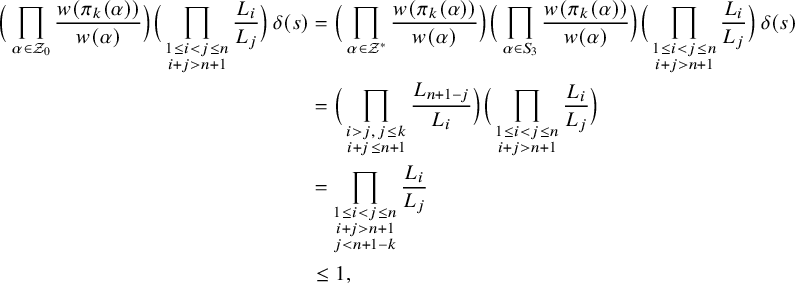 $$ \begin{align*} \begin{aligned}\Big(\prod_{\alpha\in {\mathcal{Z}}_0} \frac{w(\pi_k(\alpha))}{w(\alpha)}\Big) \Big(\prod_{\substack{1\leq i < j\leq n\\ i+j> n+1}}\frac{L_i}{L_j}\Big) \,\delta(s) &= \Big(\prod_{\alpha\in {\mathcal{Z}}^*} \frac{w(\pi_k(\alpha))}{w(\alpha)}\Big) \Big(\prod_{\alpha\in S_3} \frac{w(\pi_k(\alpha))}{w(\alpha)}\Big) \Big(\prod_{\substack{1\leq i < j\leq n\\ i+j> n+1}}\frac{L_i}{L_j}\Big) \,\delta(s) \\ &= \Big(\prod_{\substack{i>j,\,j\leq k\\i+j\leq n+1}}\frac{L_{n+1-j}}{L_i}\Big) \Big(\prod_{\substack{1\leq i < j\leq n\\ i+j> n+1}}\frac{L_i}{L_j}\Big) \\ &= \prod_{\substack{1\leq i < j\leq n\\ i+j> n+1\\ j< n +1 - k}}\frac{L_i}{L_j} \\ &\leq 1, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned}\Big(\prod_{\alpha\in {\mathcal{Z}}_0} \frac{w(\pi_k(\alpha))}{w(\alpha)}\Big) \Big(\prod_{\substack{1\leq i < j\leq n\\ i+j> n+1}}\frac{L_i}{L_j}\Big) \,\delta(s) &= \Big(\prod_{\alpha\in {\mathcal{Z}}^*} \frac{w(\pi_k(\alpha))}{w(\alpha)}\Big) \Big(\prod_{\alpha\in S_3} \frac{w(\pi_k(\alpha))}{w(\alpha)}\Big) \Big(\prod_{\substack{1\leq i < j\leq n\\ i+j> n+1}}\frac{L_i}{L_j}\Big) \,\delta(s) \\ &= \Big(\prod_{\substack{i>j,\,j\leq k\\i+j\leq n+1}}\frac{L_{n+1-j}}{L_i}\Big) \Big(\prod_{\substack{1\leq i < j\leq n\\ i+j> n+1}}\frac{L_i}{L_j}\Big) \\ &= \prod_{\substack{1\leq i < j\leq n\\ i+j> n+1\\ j< n +1 - k}}\frac{L_i}{L_j} \\ &\leq 1, \end{aligned} \end{align*} $$
where the second equality follows from Lemma 6.12, and the last inequality follows because the
![]() $L_i$
’s are nondecreasing.
$L_i$
’s are nondecreasing.
Proposition 6.3 and Lemmas 6.13 and 6.14 thus yield the bound
We now work towards obtaining a power saving.
6.3.2 Strategy towards a power saving
In light of Proposition 6.3, it is enough to have a bound of the form
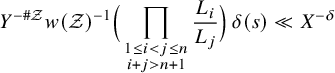 $$ \begin{align} Y^{-\#{\mathcal{Z}}}w({\mathcal{Z}})^{-1} \Big(\prod_{\substack{1\leq i < j\leq n\\ i+j> n+1}} \frac{L_i}{L_j}\Big) \,\delta(s) \ll X^{-\delta} \end{align} $$
$$ \begin{align} Y^{-\#{\mathcal{Z}}}w({\mathcal{Z}})^{-1} \Big(\prod_{\substack{1\leq i < j\leq n\\ i+j> n+1}} \frac{L_i}{L_j}\Big) \,\delta(s) \ll X^{-\delta} \end{align} $$
for some
![]() $\delta> 0$
, for all
$\delta> 0$
, for all
![]() $s\in T_{\mathcal {Z}}(L,Y).$
By modifying
$s\in T_{\mathcal {Z}}(L,Y).$
By modifying
![]() $\pi _k$
on a certain subset of
$\pi _k$
on a certain subset of
![]() ${\mathcal {Z}}$
, we are able to obtain (51) except for some
${\mathcal {Z}}$
, we are able to obtain (51) except for some
![]() $s\in T_{\mathcal {Z}}(L,Y)$
satisfying some special conditions. We then consider the contribution from these special s using a different count for
$s\in T_{\mathcal {Z}}(L,Y)$
satisfying some special conditions. We then consider the contribution from these special s using a different count for
![]() $\#\big ((s(Y{\mathcal {D}})\times s(Y{\mathcal {D}}))\cap {{\mathcal {L}}(M)} \big )$
.
$\#\big ((s(Y{\mathcal {D}})\times s(Y{\mathcal {D}}))\cap {{\mathcal {L}}(M)} \big )$
.
More precisely, let
![]() ${\mathcal {K}}_1 := \{a_{1j}: 1\leq j \leq g+2\}$
. Then
${\mathcal {K}}_1 := \{a_{1j}: 1\leq j \leq g+2\}$
. Then
![]() ${\mathcal {K}}_1$
consists exactly of those
${\mathcal {K}}_1$
consists exactly of those
![]() $\alpha \in {\mathcal {K}}$
such that the exponent of every
$\alpha \in {\mathcal {K}}$
such that the exponent of every
![]() $s_i$
is negative in
$s_i$
is negative in
![]() $w(\alpha )$
. As such, one expects that the hardest case is when
$w(\alpha )$
. As such, one expects that the hardest case is when
![]() ${\mathcal {Z}} = {\mathcal {K}}_1$
. We show first in Lemma 6.15 how to reduce to considering only
${\mathcal {Z}} = {\mathcal {K}}_1$
. We show first in Lemma 6.15 how to reduce to considering only
![]() ${\mathcal {Z}}\cap {\mathcal {K}}_1$
.
${\mathcal {Z}}\cap {\mathcal {K}}_1$
.
Lemma 6.15. Let
![]() ${\mathcal {Z}}\subset {\mathcal {Z}}_1$
be saturated with
${\mathcal {Z}}\subset {\mathcal {Z}}_1$
be saturated with
![]() $a_{11}\in {\mathcal {Z}}$
,
$a_{11}\in {\mathcal {Z}}$
,
![]() $a_{g+1,g+1}\not \in {\mathcal {Z}}$
and
$a_{g+1,g+1}\not \in {\mathcal {Z}}$
and
![]() $N({{\mathcal {L}}(M)} ,L,{\mathcal {Z}},X)> 0$
. For any
$N({{\mathcal {L}}(M)} ,L,{\mathcal {Z}},X)> 0$
. For any
![]() ${\mathcal {Z}}'\subset {\mathcal {K}}_1$
and any
${\mathcal {Z}}'\subset {\mathcal {K}}_1$
and any
![]() $s\in T'$
, we write
$s\in T'$
, we write
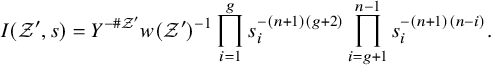 $$ \begin{align*}I({\mathcal{Z}}',s) = Y^{-\#{\mathcal{Z}}'} w({\mathcal{Z}}')^{-1}\prod_{i=1}^{g} s_i^{-(n+1)(g+2)} \prod_{i=g+1}^{n-1} s_i^{-(n+1)(n-i)}.\end{align*} $$
$$ \begin{align*}I({\mathcal{Z}}',s) = Y^{-\#{\mathcal{Z}}'} w({\mathcal{Z}}')^{-1}\prod_{i=1}^{g} s_i^{-(n+1)(g+2)} \prod_{i=g+1}^{n-1} s_i^{-(n+1)(n-i)}.\end{align*} $$
Then for any
![]() $s\in T_{\mathcal {Z}}(L,Y)$
, we have
$s\in T_{\mathcal {Z}}(L,Y)$
, we have
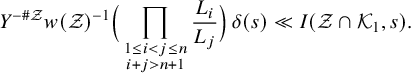 $$ \begin{align*}Y^{-\#{\mathcal{Z}}}w({\mathcal{Z}})^{-1} \Big(\prod_{\substack{1\leq i < j\leq n\\ i+j> n+1}} \frac{L_i}{L_j}\Big) \,\delta(s)\ll I({\mathcal{Z}}\cap{\mathcal{K}}_1,s).\end{align*} $$
$$ \begin{align*}Y^{-\#{\mathcal{Z}}}w({\mathcal{Z}})^{-1} \Big(\prod_{\substack{1\leq i < j\leq n\\ i+j> n+1}} \frac{L_i}{L_j}\Big) \,\delta(s)\ll I({\mathcal{Z}}\cap{\mathcal{K}}_1,s).\end{align*} $$
We then prove in Lemma 6.16 the following bound for
![]() $I({\mathcal {Z}}\cap {\mathcal {K}}_1)$
when
$I({\mathcal {Z}}\cap {\mathcal {K}}_1)$
when
![]() ${\mathcal {Z}}\cap {\mathcal {K}}_1$
is a proper subset of
${\mathcal {Z}}\cap {\mathcal {K}}_1$
is a proper subset of
![]() ${\mathcal {K}}_1$
, which gives a bound of the form (51) when
${\mathcal {K}}_1$
, which gives a bound of the form (51) when
![]() $s_n\ll Y^{1/2-\delta }$
.
$s_n\ll Y^{1/2-\delta }$
.
Lemma 6.16. Let
![]() ${\mathcal {Z}}\subset {\mathcal {Z}}_1$
be saturated with
${\mathcal {Z}}\subset {\mathcal {Z}}_1$
be saturated with
![]() $a_{11}\in {\mathcal {Z}}$
,
$a_{11}\in {\mathcal {Z}}$
,
![]() $a_{g+1,g+1}\not \in {\mathcal {Z}}$
and
$a_{g+1,g+1}\not \in {\mathcal {Z}}$
and
![]() $N({{\mathcal {L}}(M)} ,L,{\mathcal {Z}},X)> 0$
. Suppose
$N({{\mathcal {L}}(M)} ,L,{\mathcal {Z}},X)> 0$
. Suppose
![]() ${\mathcal {Z}}\cap {\mathcal {K}}_1\neq {\mathcal {K}}_1$
. For any
${\mathcal {Z}}\cap {\mathcal {K}}_1\neq {\mathcal {K}}_1$
. For any
![]() $s\in T_{\mathcal {Z}}(L,Y)$
, if
$s\in T_{\mathcal {Z}}(L,Y)$
, if
![]() $I({\mathcal {Z}}\cap {\mathcal {K}}_1,s) \gg Y^{-2\delta }$
, then
$I({\mathcal {Z}}\cap {\mathcal {K}}_1,s) \gg Y^{-2\delta }$
, then
![]() $s_n\gg Y^{1/2 - \delta }.$
$s_n\gg Y^{1/2 - \delta }.$
In the case where
![]() $s_n\gg Y^{1/2-\delta }$
, the Haar measure turns out to be very small, so we may simply ignore the singularity condition of B and prove the following bound.
$s_n\gg Y^{1/2-\delta }$
, the Haar measure turns out to be very small, so we may simply ignore the singularity condition of B and prove the following bound.
Lemma 6.17. Let
![]() ${\mathcal {Z}}\subset {\mathcal {Z}}_1$
be saturated with
${\mathcal {Z}}\subset {\mathcal {Z}}_1$
be saturated with
![]() $a_{11}\in {\mathcal {Z}}$
,
$a_{11}\in {\mathcal {Z}}$
,
![]() $a_{g+1,g+1}\not \in {\mathcal {Z}}$
and
$a_{g+1,g+1}\not \in {\mathcal {Z}}$
and
![]() $N({{\mathcal {L}}(M)} ,L,{\mathcal {Z}},X)> 0$
. Suppose
$N({{\mathcal {L}}(M)} ,L,{\mathcal {Z}},X)> 0$
. Suppose
![]() ${\mathcal {Z}}\cap {\mathcal {K}}_1\neq {\mathcal {K}}_1$
. Then for any
${\mathcal {Z}}\cap {\mathcal {K}}_1\neq {\mathcal {K}}_1$
. Then for any
![]() $s\in T_{\mathcal {Z}}(L,Y)$
with
$s\in T_{\mathcal {Z}}(L,Y)$
with
![]() $s_n\gg Y^{1/2-\delta }$
,
$s_n\gg Y^{1/2-\delta }$
,
Therefore, by taking
![]() $\delta = (n-2)/(4n^2 + 14n + 4)$
, we obtain the following result from Proposition 6.3 and Lemmas 6.15, 6.16 and 6.17:
$\delta = (n-2)/(4n^2 + 14n + 4)$
, we obtain the following result from Proposition 6.3 and Lemmas 6.15, 6.16 and 6.17:
Proposition 6.18. Let
![]() ${\mathcal {Z}}\subset {\mathcal {Z}}_1$
be saturated with
${\mathcal {Z}}\subset {\mathcal {Z}}_1$
be saturated with
![]() $a_{11}\in {\mathcal {Z}}$
,
$a_{11}\in {\mathcal {Z}}$
,
![]() $a_{g+1,g+1}\not \in {\mathcal {Z}}$
and
$a_{g+1,g+1}\not \in {\mathcal {Z}}$
and
![]() $N({{\mathcal {L}}(M)} ,L,{\mathcal {Z}},X)> 0$
. Suppose
$N({{\mathcal {L}}(M)} ,L,{\mathcal {Z}},X)> 0$
. Suppose
![]() ${\mathcal {Z}}\cap {\mathcal {K}}_1\neq {\mathcal {K}}_1$
. Then
${\mathcal {Z}}\cap {\mathcal {K}}_1\neq {\mathcal {K}}_1$
. Then
We next handle the case
![]() ${\mathcal {K}}_1\subset {\mathcal {Z}}$
. We give necessary conditions in Lemma 6.19 on s so that a bound of the form (51) does not hold.
${\mathcal {K}}_1\subset {\mathcal {Z}}$
. We give necessary conditions in Lemma 6.19 on s so that a bound of the form (51) does not hold.
Lemma 6.19. Let
![]() ${\mathcal {Z}}\subset {\mathcal {Z}}_1$
be saturated with
${\mathcal {Z}}\subset {\mathcal {Z}}_1$
be saturated with
![]() $a_{11}\in {\mathcal {Z}}$
,
$a_{11}\in {\mathcal {Z}}$
,
![]() $a_{g+1,g+1}\not \in {\mathcal {Z}}$
and
$a_{g+1,g+1}\not \in {\mathcal {Z}}$
and
![]() $N({{\mathcal {L}}(M)} ,L,{\mathcal {Z}},X)> 0$
. Suppose
$N({{\mathcal {L}}(M)} ,L,{\mathcal {Z}},X)> 0$
. Suppose
![]() ${\mathcal {K}}_1\subset {\mathcal {Z}}$
. For any
${\mathcal {K}}_1\subset {\mathcal {Z}}$
. For any
![]() $s\in T_{\mathcal {Z}}(L,Y)$
, if
$s\in T_{\mathcal {Z}}(L,Y)$
, if
![]() $I({\mathcal {K}}_1,s)\gg X^{-\delta }$
, then
$I({\mathcal {K}}_1,s)\gg X^{-\delta }$
, then
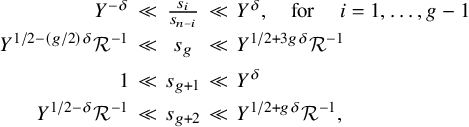 $$ \begin{align} \begin{array}{rcccl} Y^{-\delta} &\ll& \frac{s_i}{s_{n-i}} &\ll& Y^{\delta},\quad\text{for }\quad i=1,\ldots,g-1 \\[.05in] Y^{1/2-(g/2) \delta}{\mathcal{R}}^{-1}&\ll&s_g&\ll& Y^{1/2+3g\delta}{\mathcal{R}}^{-1} \\[.075in] 1&\ll&s_{g+1}&\ll&Y^{\delta} \\[.05in] Y^{1/2-\delta}{\mathcal{R}}^{-1}&\ll&s_{g+2}&\ll& Y^{1/2+g\delta}{\mathcal{R}}^{-1}, \end{array} \end{align} $$
$$ \begin{align} \begin{array}{rcccl} Y^{-\delta} &\ll& \frac{s_i}{s_{n-i}} &\ll& Y^{\delta},\quad\text{for }\quad i=1,\ldots,g-1 \\[.05in] Y^{1/2-(g/2) \delta}{\mathcal{R}}^{-1}&\ll&s_g&\ll& Y^{1/2+3g\delta}{\mathcal{R}}^{-1} \\[.075in] 1&\ll&s_{g+1}&\ll&Y^{\delta} \\[.05in] Y^{1/2-\delta}{\mathcal{R}}^{-1}&\ll&s_{g+2}&\ll& Y^{1/2+g\delta}{\mathcal{R}}^{-1}, \end{array} \end{align} $$
where
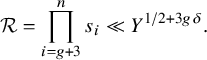 $$ \begin{align*}{\mathcal{R}} = \prod_{i=g+3}^n s_i \ll Y^{1/2+3g\delta}.\end{align*} $$
$$ \begin{align*}{\mathcal{R}} = \prod_{i=g+3}^n s_i \ll Y^{1/2+3g\delta}.\end{align*} $$
Note that the coefficients of
![]() $\delta $
in the exponents in the above bounds are not optimal and are simply chosen to make the formula look nice. The optimal coefficients can be obtained from the proof.
$\delta $
in the exponents in the above bounds are not optimal and are simply chosen to make the formula look nice. The optimal coefficients can be obtained from the proof.
When s satisfies (52), we give further conditions in Lemma 6.20 on s so that simply using the Haar measure and ignoring the singularity condition by counting all symmetric matrices is not enough for a power saving.
Lemma 6.20. Let
![]() ${\mathcal {Z}}\subset {\mathcal {Z}}_1$
be saturated with
${\mathcal {Z}}\subset {\mathcal {Z}}_1$
be saturated with
![]() $a_{11}\in {\mathcal {Z}}$
,
$a_{11}\in {\mathcal {Z}}$
,
![]() $a_{g+1,g+1}\not \in {\mathcal {Z}}$
and
$a_{g+1,g+1}\not \in {\mathcal {Z}}$
and
![]() $N({{\mathcal {L}}(M)} ,L,{\mathcal {Z}},X)> 0$
. Suppose
$N({{\mathcal {L}}(M)} ,L,{\mathcal {Z}},X)> 0$
. Suppose
![]() ${\mathcal {K}}_1\subset {\mathcal {Z}}$
. For any
${\mathcal {K}}_1\subset {\mathcal {Z}}$
. For any
![]() $s\in T_{\mathcal {Z}}(L,Y)$
, if
$s\in T_{\mathcal {Z}}(L,Y)$
, if
then
To obtain a further saving, we need to use the
![]() $|q|$
-invariant!
$|q|$
-invariant!
Lemma 6.21. Suppose
![]() $M>X^\eta $
where
$M>X^\eta $
where
![]() $\eta>0$
is some fixed constant. Let
$\eta>0$
is some fixed constant. Let
![]() ${\mathcal {Z}}\subset {\mathcal {Z}}_1$
be saturated with
${\mathcal {Z}}\subset {\mathcal {Z}}_1$
be saturated with
![]() $a_{11}\in {\mathcal {Z}}$
,
$a_{11}\in {\mathcal {Z}}$
,
![]() $a_{g+1,g+1}\not \in {\mathcal {Z}}$
and
$a_{g+1,g+1}\not \in {\mathcal {Z}}$
and
![]() $N({{\mathcal {L}}(M)} ,L,{\mathcal {Z}},X)> 0$
. Suppose
$N({{\mathcal {L}}(M)} ,L,{\mathcal {Z}},X)> 0$
. Suppose
![]() ${\mathcal {K}}_1\subset {\mathcal {Z}}$
. Then for
${\mathcal {K}}_1\subset {\mathcal {Z}}$
. Then for
![]() $\delta < \min (\eta ,1)/(1355g^6)$
and any
$\delta < \min (\eta ,1)/(1355g^6)$
and any
![]() $s\in T_{\mathcal {Z}}(L,Y)$
such that (52) and (53) hold, we have
$s\in T_{\mathcal {Z}}(L,Y)$
such that (52) and (53) hold, we have
Therefore, by taking
![]() $\delta = 64\min (\eta ,1)/(1355n^6)$
, we obtain the following result from Proposition 6.3 and Lemmas 6.15, 6.19, 6.20 and 6.21.
$\delta = 64\min (\eta ,1)/(1355n^6)$
, we obtain the following result from Proposition 6.3 and Lemmas 6.15, 6.19, 6.20 and 6.21.
Proposition 6.22. Suppose
![]() $M>X^\eta $
where
$M>X^\eta $
where
![]() $\eta>0$
is some fixed constant. Let
$\eta>0$
is some fixed constant. Let
![]() ${\mathcal {Z}}\subset {\mathcal {Z}}_1$
be saturated with
${\mathcal {Z}}\subset {\mathcal {Z}}_1$
be saturated with
![]() $a_{11}\in {\mathcal {Z}}$
,
$a_{11}\in {\mathcal {Z}}$
,
![]() $a_{g+1,g+1}\not \in {\mathcal {Z}}$
and
$a_{g+1,g+1}\not \in {\mathcal {Z}}$
and
![]() $N({{\mathcal {L}}(M)} ,L,{\mathcal {Z}},X)> 0$
. Suppose
$N({{\mathcal {L}}(M)} ,L,{\mathcal {Z}},X)> 0$
. Suppose
![]() ${\mathcal {K}}_1\subset {\mathcal {Z}}$
. Then
${\mathcal {K}}_1\subset {\mathcal {Z}}$
. Then
Theorem 6.11 then follows immediately from (40), Proposition 6.18, Proposition 6.22 and summing over the
![]() $O(1)$
different possible
$O(1)$
different possible
![]() ${\mathcal {Z}}$
’s and the
${\mathcal {Z}}$
’s and the
![]() $O(Y^\epsilon )$
different possible L’s.
$O(Y^\epsilon )$
different possible L’s.
6.3.3 Proofs of Lemmas 6.15, 6.16, 6.17, 6.19, 6.20 and 6.21.
We fix a saturated
![]() ${\mathcal {Z}}\subset {\mathcal {Z}}_1$
with
${\mathcal {Z}}\subset {\mathcal {Z}}_1$
with
![]() $a_{11}\in {\mathcal {Z}}$
,
$a_{11}\in {\mathcal {Z}}$
,
![]() $a_{g+1,g+1}\not \in {\mathcal {Z}}$
and
$a_{g+1,g+1}\not \in {\mathcal {Z}}$
and
![]() $N({{\mathcal {L}}(M)} ,L,{\mathcal {Z}},X)> 0$
.
$N({{\mathcal {L}}(M)} ,L,{\mathcal {Z}},X)> 0$
.
Proof of Lemma 6.15.
Recall that
![]() ${\mathcal {K}}_1 := \{a_{1j}: 1\leq j \leq g+2\}$
. Let
${\mathcal {K}}_1 := \{a_{1j}: 1\leq j \leq g+2\}$
. Let
![]() $k\in \{1,\ldots ,g\}$
be the largest integer such that
$k\in \{1,\ldots ,g\}$
be the largest integer such that
![]() $a_{kk}\notin {\mathcal {Z}}$
. Then, applying Lemma 6.14 to the saturated set
$a_{kk}\notin {\mathcal {Z}}$
. Then, applying Lemma 6.14 to the saturated set
![]() ${\mathcal {Z}}\cup {\mathcal {K}}_1$
, we have
${\mathcal {Z}}\cup {\mathcal {K}}_1$
, we have
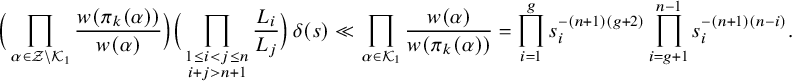 $$ \begin{align*} \Big(\prod_{\alpha\in {\mathcal{Z}}\backslash {\mathcal{K}}_1} \frac{w(\pi_k(\alpha))}{w(\alpha)}\Big) \Big(\prod_{\substack{1\leq i < j\leq n\\ i+j> n+1}} \frac{L_i}{L_j}\Big) \,\delta(s) \ll \prod_{\alpha \in {\mathcal{K}}_1} \frac{w(\alpha)}{w(\pi_k(\alpha))} =\prod_{i=1}^{g} s_i^{-(n+1)(g+2)}\prod_{i=g+1}^{n-1} s_i^{-(n+1)(n-i)}. \end{align*} $$
$$ \begin{align*} \Big(\prod_{\alpha\in {\mathcal{Z}}\backslash {\mathcal{K}}_1} \frac{w(\pi_k(\alpha))}{w(\alpha)}\Big) \Big(\prod_{\substack{1\leq i < j\leq n\\ i+j> n+1}} \frac{L_i}{L_j}\Big) \,\delta(s) \ll \prod_{\alpha \in {\mathcal{K}}_1} \frac{w(\alpha)}{w(\pi_k(\alpha))} =\prod_{i=1}^{g} s_i^{-(n+1)(g+2)}\prod_{i=g+1}^{n-1} s_i^{-(n+1)(n-i)}. \end{align*} $$
Hence, by Lemma 6.13, we obtain for any
![]() $s\in T_{\mathcal {Z}}(L,Y)$
,
$s\in T_{\mathcal {Z}}(L,Y)$
,
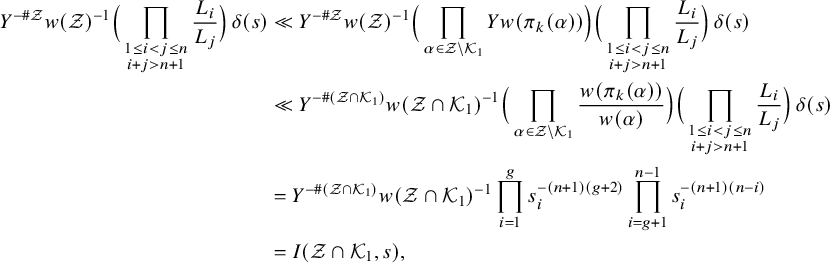 $$ \begin{align*} Y^{-\#{\mathcal{Z}}}w({\mathcal{Z}})^{-1} \Big(\prod_{\substack{1\leq i < j\leq n\\ i+j> n+1}} \frac{L_i}{L_j}\Big) \,\delta(s)&\ll Y^{-\#{\mathcal{Z}}}w({\mathcal{Z}})^{-1}\Big(\prod_{\alpha\in{\mathcal{Z}}\backslash{\mathcal{K}}_1} Yw(\pi_k(\alpha))\Big) \Big(\prod_{\substack{1\leq i < j\leq n\\ i+j> n+1}} \frac{L_i}{L_j}\Big) \,\delta(s) \\&\ll Y^{-\#({\mathcal{Z}}\cap{\mathcal{K}}_1)}w({\mathcal{Z}}\cap {\mathcal{K}}_1)^{-1}\Big(\prod_{\alpha\in{\mathcal{Z}}\backslash{\mathcal{K}}_1} \frac{w(\pi_k(\alpha))}{w(\alpha)}\Big) \Big(\prod_{\substack{1\leq i < j\leq n\\ i+j> n+1}} \frac{L_i}{L_j}\Big) \,\delta(s) \\&= Y^{-\#({\mathcal{Z}}\cap{\mathcal{K}}_1)} w({\mathcal{Z}}\cap{\mathcal{K}}_1)^{-1}\prod_{i=1}^{g} s_i^{-(n+1)(g+2)} \prod_{i=g+1}^{n-1} s_i^{-(n+1)(n-i)}\\&= I({\mathcal{Z}}\cap{\mathcal{K}}_1,s), \end{align*} $$
$$ \begin{align*} Y^{-\#{\mathcal{Z}}}w({\mathcal{Z}})^{-1} \Big(\prod_{\substack{1\leq i < j\leq n\\ i+j> n+1}} \frac{L_i}{L_j}\Big) \,\delta(s)&\ll Y^{-\#{\mathcal{Z}}}w({\mathcal{Z}})^{-1}\Big(\prod_{\alpha\in{\mathcal{Z}}\backslash{\mathcal{K}}_1} Yw(\pi_k(\alpha))\Big) \Big(\prod_{\substack{1\leq i < j\leq n\\ i+j> n+1}} \frac{L_i}{L_j}\Big) \,\delta(s) \\&\ll Y^{-\#({\mathcal{Z}}\cap{\mathcal{K}}_1)}w({\mathcal{Z}}\cap {\mathcal{K}}_1)^{-1}\Big(\prod_{\alpha\in{\mathcal{Z}}\backslash{\mathcal{K}}_1} \frac{w(\pi_k(\alpha))}{w(\alpha)}\Big) \Big(\prod_{\substack{1\leq i < j\leq n\\ i+j> n+1}} \frac{L_i}{L_j}\Big) \,\delta(s) \\&= Y^{-\#({\mathcal{Z}}\cap{\mathcal{K}}_1)} w({\mathcal{Z}}\cap{\mathcal{K}}_1)^{-1}\prod_{i=1}^{g} s_i^{-(n+1)(g+2)} \prod_{i=g+1}^{n-1} s_i^{-(n+1)(n-i)}\\&= I({\mathcal{Z}}\cap{\mathcal{K}}_1,s), \end{align*} $$
as desired.
Note that a direct computation yields
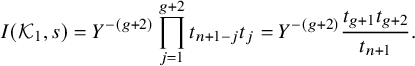 $$ \begin{align} I({\mathcal{K}}_1,s) = Y^{-(g+2)}\prod_{j=1}^{g+2}t_{n+1-j}t_j= Y^{-(g+2)}\frac{t_{g+1}t_{g+2}}{t_{n+1}}. \end{align} $$
$$ \begin{align} I({\mathcal{K}}_1,s) = Y^{-(g+2)}\prod_{j=1}^{g+2}t_{n+1-j}t_j= Y^{-(g+2)}\frac{t_{g+1}t_{g+2}}{t_{n+1}}. \end{align} $$
Proof of Lemma 6.16.
Since
![]() ${\mathcal {Z}}$
is saturated and
${\mathcal {Z}}$
is saturated and
![]() ${\mathcal {Z}}\cap {\mathcal {K}}_1\neq {\mathcal {K}}_1$
, we have
${\mathcal {Z}}\cap {\mathcal {K}}_1\neq {\mathcal {K}}_1$
, we have
![]() ${\mathcal {Z}}\cap {\mathcal {K}}_1 = \{a_{11},\ldots ,a_{1j}\}$
for some
${\mathcal {Z}}\cap {\mathcal {K}}_1 = \{a_{11},\ldots ,a_{1j}\}$
for some
![]() $j=1,\ldots ,g+1$
. Since
$j=1,\ldots ,g+1$
. Since
![]() $a_{g+1,g+1}$
and
$a_{g+1,g+1}$
and
![]() $a_{1,g+2}$
do not belong to
$a_{1,g+2}$
do not belong to
![]() ${\mathcal {Z}}$
, we have for
${\mathcal {Z}}$
, we have for
![]() $s\in T_{\mathcal {Z}}(L,Y)$
,
$s\in T_{\mathcal {Z}}(L,Y)$
,
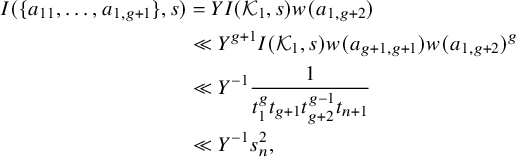 $$ \begin{align*} \begin{aligned} I(\{a_{11},\ldots,a_{1,g+1}\},s)&=YI({\mathcal{K}}_1,s)w(a_{1,g+2}) \\ &\ll Y^{g+1}I({\mathcal{K}}_1,s)w(a_{g+1,g+1})w(a_{1,g+2})^{g} \\ &\ll Y^{-1}\frac{1}{t_1^gt_{g+1}t_{g+2}^{g-1}t_{n+1}} \\ &\ll Y^{-1}s_n^2, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} I(\{a_{11},\ldots,a_{1,g+1}\},s)&=YI({\mathcal{K}}_1,s)w(a_{1,g+2}) \\ &\ll Y^{g+1}I({\mathcal{K}}_1,s)w(a_{g+1,g+1})w(a_{1,g+2})^{g} \\ &\ll Y^{-1}\frac{1}{t_1^gt_{g+1}t_{g+2}^{g-1}t_{n+1}} \\ &\ll Y^{-1}s_n^2, \end{aligned} \end{align*} $$
since the powers of the
![]() $s_i$
’s in the third line are negative for
$s_i$
’s in the third line are negative for
![]() $i<n$
.
$i<n$
.
Similarly, for any
![]() $j=1,\ldots ,g$
, we compute
$j=1,\ldots ,g$
, we compute
as desired.
Proof of Lemma 6.17.
Suppose now
![]() $s_n\gg Y^{1/2-\delta }$
. First note, that the inequality
$s_n\gg Y^{1/2-\delta }$
. First note, that the inequality
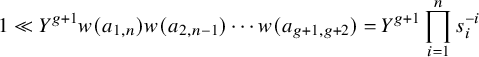 $$ \begin{align} 1\ll Y^{g+1}w(a_{1,n})w(a_{2,n-1})\cdots w(a_{g+1,g+2}) = Y^{g+1}\prod_{i=1}^n s_i^{-i} \end{align} $$
$$ \begin{align} 1\ll Y^{g+1}w(a_{1,n})w(a_{2,n-1})\cdots w(a_{g+1,g+2}) = Y^{g+1}\prod_{i=1}^n s_i^{-i} \end{align} $$
implies that we have
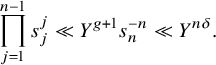 $$ \begin{align} \prod_{j=1}^{n-1} s_j^{j}\ll Y^{g+1}s_n^{-n}\ll Y^{n\delta}. \end{align} $$
$$ \begin{align} \prod_{j=1}^{n-1} s_j^{j}\ll Y^{g+1}s_n^{-n}\ll Y^{n\delta}. \end{align} $$
Since each
![]() $s_i\gg 1$
, we also have
$s_i\gg 1$
, we also have
![]() $s_n\ll Y^{1/2}$
by (56). Hence,
$s_n\ll Y^{1/2}$
by (56). Hence,
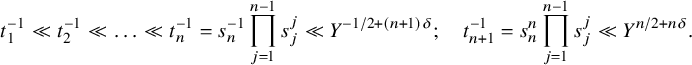 $$ \begin{align*} t_1^{-1}\ll t_2^{-1}\ll\ldots\ll t_{n}^{-1} = s_n^{-1}\prod_{j=1}^{n-1} s_j^{j}\ll Y^{-1/2+(n+1)\delta};\quad t_{n+1}^{-1}=s_n^n\prod_{j=1}^{n-1} s_j^{j}\ll Y^{n/2 + n\delta}. \end{align*} $$
$$ \begin{align*} t_1^{-1}\ll t_2^{-1}\ll\ldots\ll t_{n}^{-1} = s_n^{-1}\prod_{j=1}^{n-1} s_j^{j}\ll Y^{-1/2+(n+1)\delta};\quad t_{n+1}^{-1}=s_n^n\prod_{j=1}^{n-1} s_j^{j}\ll Y^{n/2 + n\delta}. \end{align*} $$
Thus,
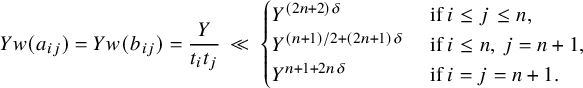 $$ \begin{align*} Yw(a_{ij})=Yw(b_{ij})=\frac{Y}{t_it_j}\,\ll\, \begin{cases} Y^{(2n+2)\delta}&\text{ if }i\leq j\leq n,\\ Y^{(n+1)/2+(2n+1)\delta}&\text{ if }i\leq n,\,j= n+1,\\ Y^{n+1+2n\delta}&\text{ if }i=j=n+1. \end{cases} \end{align*} $$
$$ \begin{align*} Yw(a_{ij})=Yw(b_{ij})=\frac{Y}{t_it_j}\,\ll\, \begin{cases} Y^{(2n+2)\delta}&\text{ if }i\leq j\leq n,\\ Y^{(n+1)/2+(2n+1)\delta}&\text{ if }i\leq n,\,j= n+1,\\ Y^{n+1+2n\delta}&\text{ if }i=j=n+1. \end{cases} \end{align*} $$
Multiplying these weights together and applying Proposition 4.1 gives the estimate
Meanwhile, in this region where
![]() $s_n\geq X^{1/2-\delta }$
, the quantity
$s_n\geq X^{1/2-\delta }$
, the quantity
![]() $\delta (s)$
satisfies
$\delta (s)$
satisfies
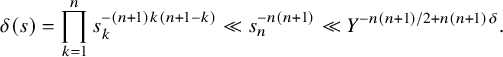 $$ \begin{align} \delta(s)=\prod_{k=1}^{n}s_k^{-(n+1)k(n+1-k)} \ll s_n^{-n(n+1)}\ll Y^{-n(n+1)/2 + n(n+1)\delta}. \end{align} $$
$$ \begin{align} \delta(s)=\prod_{k=1}^{n}s_k^{-(n+1)k(n+1-k)} \ll s_n^{-n(n+1)}\ll Y^{-n(n+1)/2 + n(n+1)\delta}. \end{align} $$
Multiplying the bounds in (57) and (58) together yields
as desired.
Proof of Lemma 6.19.
Suppose now
![]() ${\mathcal {K}}_1\subset {\mathcal {Z}}\subset {\mathcal {Z}}_1$
and
${\mathcal {K}}_1\subset {\mathcal {Z}}\subset {\mathcal {Z}}_1$
and
![]() $I({\mathcal {K}}_1,s) \gg X^{-\delta }$
for some
$I({\mathcal {K}}_1,s) \gg X^{-\delta }$
for some
![]() $s\in T_{\mathcal {Z}}(L,Y)$
. We prove first that for any
$s\in T_{\mathcal {Z}}(L,Y)$
. We prove first that for any
![]() $i = 1,\ldots ,g-1$
, we have
$i = 1,\ldots ,g-1$
, we have
Indeed, since
![]() $a_{j,n+1-j}\notin {\mathcal {Z}}$
for all j, we have from (54) that, for any
$a_{j,n+1-j}\notin {\mathcal {Z}}$
for all j, we have from (54) that, for any
![]() $k = 1,\ldots ,g$
,
$k = 1,\ldots ,g$
,
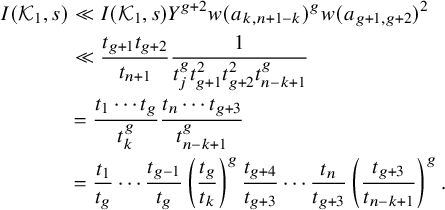 $$ \begin{align*} \begin{aligned} I({\mathcal{K}}_1,s)&\ll I({\mathcal{K}}_1,s) Y^{g+2}w(a_{k,n+1-k})^gw(a_{g+1,g+2})^2 \\&\ll \frac{t_{g+1}t_{g+2}}{t_{n+1}}\frac{1}{t_j^{g}t_{g+1}^2t_{g+2}^2t_{n-k+1}^g} \\ &= \frac{t_1\cdots t_g}{t_k^g}\frac{t_n\cdots t_{g+3}}{t_{n-k+1}^g} \\ &= \frac{t_1}{t_g}\cdots \frac{t_{g-1}}{t_g}\left(\frac{t_g}{t_k}\right)^g\frac{t_{g+4}}{t_{g+3}}\cdots \frac{t_n}{t_{g+3}}\left(\frac{t_{g+3}}{t_{n-k+1}}\right)^g. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} I({\mathcal{K}}_1,s)&\ll I({\mathcal{K}}_1,s) Y^{g+2}w(a_{k,n+1-k})^gw(a_{g+1,g+2})^2 \\&\ll \frac{t_{g+1}t_{g+2}}{t_{n+1}}\frac{1}{t_j^{g}t_{g+1}^2t_{g+2}^2t_{n-k+1}^g} \\ &= \frac{t_1\cdots t_g}{t_k^g}\frac{t_n\cdots t_{g+3}}{t_{n-k+1}^g} \\ &= \frac{t_1}{t_g}\cdots \frac{t_{g-1}}{t_g}\left(\frac{t_g}{t_k}\right)^g\frac{t_{g+4}}{t_{g+3}}\cdots \frac{t_n}{t_{g+3}}\left(\frac{t_{g+3}}{t_{n-k+1}}\right)^g. \end{aligned} \end{align*} $$
Hence,
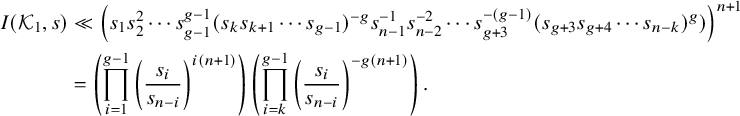 $$ \begin{align*} \begin{aligned} I({\mathcal{K}}_1,s)&\ll \left(s_1s_2^2\cdots s_{g-1}^{g-1}(s_ks_{k+1}\cdots s_{g-1})^{-g}s_{n-1}^{-1}s_{n-2}^{-2}\cdots s_{g+3}^{-(g-1)}(s_{g+3}s_{g+4}\cdots s_{n-k})^g)\right)^{n+1} \\ &= \left(\prod_{i=1}^{g-1}\left(\frac{s_i}{s_{n-i}}\right)^{i(n+1)}\right)\left(\prod_{i=k}^{g-1}\left(\frac{s_i}{s_{n-i}}\right)^{-g(n+1)}\right). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} I({\mathcal{K}}_1,s)&\ll \left(s_1s_2^2\cdots s_{g-1}^{g-1}(s_ks_{k+1}\cdots s_{g-1})^{-g}s_{n-1}^{-1}s_{n-2}^{-2}\cdots s_{g+3}^{-(g-1)}(s_{g+3}s_{g+4}\cdots s_{n-k})^g)\right)^{n+1} \\ &= \left(\prod_{i=1}^{g-1}\left(\frac{s_i}{s_{n-i}}\right)^{i(n+1)}\right)\left(\prod_{i=k}^{g-1}\left(\frac{s_i}{s_{n-i}}\right)^{-g(n+1)}\right). \end{aligned} \end{align*} $$
Denote the product of the two factors in the final line by
![]() $J_k$
. Then
$J_k$
. Then
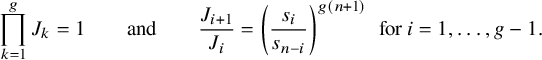 $$ \begin{align*}\prod_{k=1}^g J_k= 1\qquad\text{and}\qquad \frac{J_{i+1}}{J_{i}}= \left(\frac{s_i}{s_{n-i}}\right)^{g(n+1)}\,\text{ for }i=1,\ldots,g-1. \end{align*} $$
$$ \begin{align*}\prod_{k=1}^g J_k= 1\qquad\text{and}\qquad \frac{J_{i+1}}{J_{i}}= \left(\frac{s_i}{s_{n-i}}\right)^{g(n+1)}\,\text{ for }i=1,\ldots,g-1. \end{align*} $$
Since, by assumption,
![]() $I({\mathcal {K}}_1,s)\gg X^{-\delta }$
, we have
$I({\mathcal {K}}_1,s)\gg X^{-\delta }$
, we have
![]() $J_k\gg Y^{-(n+1)\delta }$
for every
$J_k\gg Y^{-(n+1)\delta }$
for every
![]() $k=1,\ldots ,g$
. Therefore, for every
$k=1,\ldots ,g$
. Therefore, for every
![]() $i=1,\ldots ,g-1$
, we have
$i=1,\ldots ,g-1$
, we have
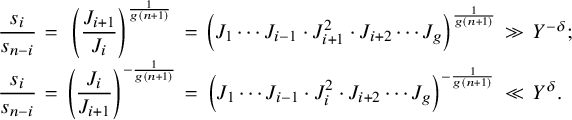 $$ \begin{align*}\begin{array}{rcccccl}\displaystyle \frac{s_i}{s_{n-i}}&=& \displaystyle\left(\frac{J_{i+1}}{J_i}\right)^{\frac{1}{g(n+1)}}&=&\displaystyle \left(J_1\cdots J_{i-1}\cdot J_{i+1}^2\cdot J_{i+2}\cdots J_g\right)^{\frac{1}{g(n+1)}}&\gg&Y^{-\delta}; \\[.1in] \displaystyle\frac{s_i}{s_{n-i}}&=&\displaystyle \left(\frac{J_{i}}{J_{i+1}}\right)^{-\frac{1}{g(n+1)}}&=& \displaystyle\left(J_1\cdots J_{i-1}\cdot J_{i}^2\cdot J_{i+2}\cdots J_g\right)^{-\frac{1}{g(n+1)}}&\ll&Y^{\delta}.\end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{rcccccl}\displaystyle \frac{s_i}{s_{n-i}}&=& \displaystyle\left(\frac{J_{i+1}}{J_i}\right)^{\frac{1}{g(n+1)}}&=&\displaystyle \left(J_1\cdots J_{i-1}\cdot J_{i+1}^2\cdot J_{i+2}\cdots J_g\right)^{\frac{1}{g(n+1)}}&\gg&Y^{-\delta}; \\[.1in] \displaystyle\frac{s_i}{s_{n-i}}&=&\displaystyle \left(\frac{J_{i}}{J_{i+1}}\right)^{-\frac{1}{g(n+1)}}&=& \displaystyle\left(J_1\cdots J_{i-1}\cdot J_{i}^2\cdot J_{i+2}\cdots J_g\right)^{-\frac{1}{g(n+1)}}&\ll&Y^{\delta}.\end{array} \end{align*} $$
The claimed bound (59) follows.
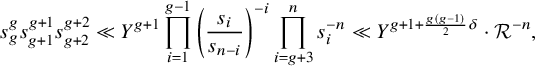 $$ \begin{align} s_g^gs_{g+1}^{g+1}s_{g+2}^{g+2} \ll Y^{g+1}\prod_{i=1}^{g-1}\left(\frac{s_i}{s_{n-i}}\right)^{-i}\prod_{i=g+3}^ns_i^{-n} \ll Y^{g+1+\frac{g(g-1)}{2}\delta}\cdot {\mathcal{R}}^{-n}, \end{align} $$
$$ \begin{align} s_g^gs_{g+1}^{g+1}s_{g+2}^{g+2} \ll Y^{g+1}\prod_{i=1}^{g-1}\left(\frac{s_i}{s_{n-i}}\right)^{-i}\prod_{i=g+3}^ns_i^{-n} \ll Y^{g+1+\frac{g(g-1)}{2}\delta}\cdot {\mathcal{R}}^{-n}, \end{align} $$
where
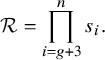 $$ \begin{align*}{\mathcal{R}}=\prod_{i=g+3}^ns_i.\end{align*} $$
$$ \begin{align*}{\mathcal{R}}=\prod_{i=g+3}^ns_i.\end{align*} $$
We next prove the desired lower bounds:
The bound
![]() $s_{g+1}\gg 1$
follows from the definition of
$s_{g+1}\gg 1$
follows from the definition of
![]() $T'$
. For the bounds on
$T'$
. For the bounds on
![]() $s_g$
and
$s_g$
and
![]() $s_{g+2}$
, we use the assumption that
$s_{g+2}$
, we use the assumption that
![]() $a_{g+1,g+1}\notin {\mathcal {Z}}$
and the computation of
$a_{g+1,g+1}\notin {\mathcal {Z}}$
and the computation of
![]() $I({\mathcal {K}}_1,s)$
in (54) to obtain
$I({\mathcal {K}}_1,s)$
in (54) to obtain
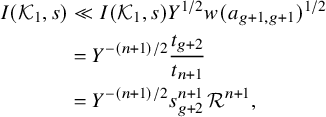 $$ \begin{align*} \begin{aligned} I({\mathcal{K}}_1,s) &\ll I({\mathcal{K}}_1,s)Y^{1/2}w(a_{g+1,g+1})^{1/2} \\ &= Y^{-(n+1)/2}\frac{t_{g+2}}{t_{n+1}} \\ &= Y^{-(n+1)/2}s_{g+2}^{n+1}\,{\mathcal{R}}^{n+1}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} I({\mathcal{K}}_1,s) &\ll I({\mathcal{K}}_1,s)Y^{1/2}w(a_{g+1,g+1})^{1/2} \\ &= Y^{-(n+1)/2}\frac{t_{g+2}}{t_{n+1}} \\ &= Y^{-(n+1)/2}s_{g+2}^{n+1}\,{\mathcal{R}}^{n+1}, \end{aligned} \end{align*} $$
which along with
![]() $I({\mathcal {K}}_1,s)\gg Y^{-(n+1)\delta }$
implies the desired lower bounds on
$I({\mathcal {K}}_1,s)\gg Y^{-(n+1)\delta }$
implies the desired lower bounds on
![]() $s_{g+2}$
; and
$s_{g+2}$
; and
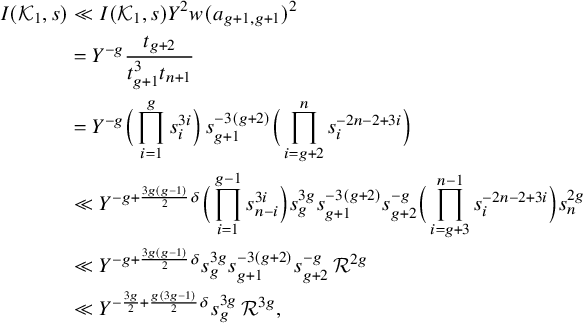 $$ \begin{align*} I({\mathcal{K}}_1,s)&\ll I({\mathcal{K}}_1,s)Y^2w(a_{g+1,g+1})^2 \\ &= Y^{-g}\frac{t_{g+2}}{t_{g+1}^3t_{n+1}} \\ &= Y^{-g}\Big(\prod_{i=1}^g s_i^{3i}\Big)\, s_{g+1}^{-3(g+2)}\Big(\prod_{i=g+2}^{n}s_i^{-2n-2+3i}\Big) \\ &\ll Y^{-g+\frac{3g(g-1)}{2}\delta}\Big(\prod_{i=1}^{g-1} s_{n-i}^{3i}\Big) s_g^{3g}s_{g+1}^{-3(g+2)}s_{g+2}^{-g} \Big(\prod_{i=g+3}^{n-1}s_i^{-2n-2+3i}\Big) s_n^{2g} \\ &\ll Y^{-g+\frac{3g(g-1)}{2}\delta}s_g^{3g}s_{g+1}^{-3(g+2)}s_{g+2}^{-g}\,{\mathcal{R}}^{2g} \\ &\ll Y^{-\frac{3g}{2} + \frac{g(3g-1)}{2}\delta}s_g^{3g}\,{\mathcal{R}}^{3g}, \end{align*} $$
$$ \begin{align*} I({\mathcal{K}}_1,s)&\ll I({\mathcal{K}}_1,s)Y^2w(a_{g+1,g+1})^2 \\ &= Y^{-g}\frac{t_{g+2}}{t_{g+1}^3t_{n+1}} \\ &= Y^{-g}\Big(\prod_{i=1}^g s_i^{3i}\Big)\, s_{g+1}^{-3(g+2)}\Big(\prod_{i=g+2}^{n}s_i^{-2n-2+3i}\Big) \\ &\ll Y^{-g+\frac{3g(g-1)}{2}\delta}\Big(\prod_{i=1}^{g-1} s_{n-i}^{3i}\Big) s_g^{3g}s_{g+1}^{-3(g+2)}s_{g+2}^{-g} \Big(\prod_{i=g+3}^{n-1}s_i^{-2n-2+3i}\Big) s_n^{2g} \\ &\ll Y^{-g+\frac{3g(g-1)}{2}\delta}s_g^{3g}s_{g+1}^{-3(g+2)}s_{g+2}^{-g}\,{\mathcal{R}}^{2g} \\ &\ll Y^{-\frac{3g}{2} + \frac{g(3g-1)}{2}\delta}s_g^{3g}\,{\mathcal{R}}^{3g}, \end{align*} $$
implying the desired lower bound on
![]() $s_g$
, where in the last inequality we used the already-established lower bounds on
$s_g$
, where in the last inequality we used the already-established lower bounds on
![]() $s_{g+1}$
and
$s_{g+1}$
and
![]() $s_{g+2}$
.
$s_{g+2}$
.
The desired lower bounds for
![]() $s_g$
,
$s_g$
,
![]() $s_{g+1}$
,
$s_{g+1}$
,
![]() $s_{g+2}$
then follow by combining the upper bound on
$s_{g+2}$
then follow by combining the upper bound on
![]() $s_g^gs_{g+1}^{g+1}s_{g+2}^{g+2}$
in (60) and the individual lower bounds on
$s_g^gs_{g+1}^{g+1}s_{g+2}^{g+2}$
in (60) and the individual lower bounds on
![]() $s_g$
,
$s_g$
,
![]() $s_{g+1}$
,
$s_{g+1}$
,
![]() $s_{g+2}$
in (61). The desired upper bound on
$s_{g+2}$
in (61). The desired upper bound on
![]() ${\mathcal {R}}$
follows by comparing the upper bound on
${\mathcal {R}}$
follows by comparing the upper bound on
![]() $s_g$
and the trivial lower bound
$s_g$
and the trivial lower bound
![]() $s_g\gg 1$
.
$s_g\gg 1$
.
Proof of Lemma 6.20.
Suppose
![]() ${\mathcal {K}}_1\subset {\mathcal {Z}}$
and
${\mathcal {K}}_1\subset {\mathcal {Z}}$
and
![]() $s\in T_{\mathcal {Z}}(L,Y)$
satisfies (52). Then
$s\in T_{\mathcal {Z}}(L,Y)$
satisfies (52). Then
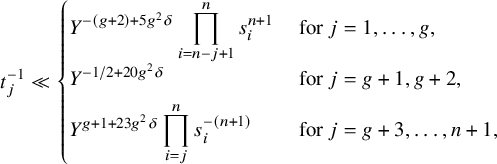 $$ \begin{align} t_j^{-1} \ll\begin{cases}\displaystyle Y^{-(g+2)+5g^2\delta}\prod_{i=n-j+1}^n s_i^{n+1}&\text{ for }j=1,\ldots,g,\\[4pt] \displaystyle Y^{-1/2+ 20g^2\delta}&\text{ for }j=g+1,g+2,\\[4pt] \displaystyle Y^{g+1+23g^2\delta}\prod_{i=j}^n s_i^{-(n+1)}&\text{ for }j = g+3,\ldots,n+1, \end{cases} \end{align} $$
$$ \begin{align} t_j^{-1} \ll\begin{cases}\displaystyle Y^{-(g+2)+5g^2\delta}\prod_{i=n-j+1}^n s_i^{n+1}&\text{ for }j=1,\ldots,g,\\[4pt] \displaystyle Y^{-1/2+ 20g^2\delta}&\text{ for }j=g+1,g+2,\\[4pt] \displaystyle Y^{g+1+23g^2\delta}\prod_{i=j}^n s_i^{-(n+1)}&\text{ for }j = g+3,\ldots,n+1, \end{cases} \end{align} $$
where the upper bound on
![]() ${\mathcal {R}}$
also gives
${\mathcal {R}}$
also gives
![]() $t_j^{-1} \ll Y^{-1/2+20g^2\delta }$
for
$t_j^{-1} \ll Y^{-1/2+20g^2\delta }$
for
![]() $j = 1,\ldots ,g$
. For
$j = 1,\ldots ,g$
. For
![]() $i,j\leq g+2$
, we have
$i,j\leq g+2$
, we have
![]() $Yt_i^{-1}t_j^{-1}\ll Y^{40g^2\delta }$
. For
$Yt_i^{-1}t_j^{-1}\ll Y^{40g^2\delta }$
. For
![]() $j\geq g+3$
and
$j\geq g+3$
and
![]() $i\leq n-j+1$
, we have
$i\leq n-j+1$
, we have
![]() $Yt_i^{-1}t_j^{-1}\ll Y^{28g^2\delta }$
. Using (62) for the rest of the coordinates gives
$Yt_i^{-1}t_j^{-1}\ll Y^{28g^2\delta }$
. Using (62) for the rest of the coordinates gives
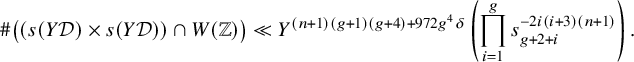 $$ \begin{align*}\#\big((s(Y{\mathcal{D}})\times s(Y{\mathcal{D}}))\cap W({\mathbb{Z}})\big) \ll Y^{(n+1)(g+1)(g+4) + 972g^4\delta}\left( \prod_{i=1}^{g} s_{g+2+i}^{-2i(i+3)(n+1)}\right).\end{align*} $$
$$ \begin{align*}\#\big((s(Y{\mathcal{D}})\times s(Y{\mathcal{D}}))\cap W({\mathbb{Z}})\big) \ll Y^{(n+1)(g+1)(g+4) + 972g^4\delta}\left( \prod_{i=1}^{g} s_{g+2+i}^{-2i(i+3)(n+1)}\right).\end{align*} $$
The Haar measure satisfies the following bound:
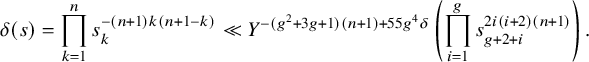 $$ \begin{align*}\delta(s)=\prod_{k=1}^{n}s_k^{-(n+1)k(n+1-k)} \ll Y^{-(g^2 + 3g + 1)(n+1) + 55g^4\delta}\left(\prod_{i=1}^{g} s_{g+2+i}^{2i(i+2)(n+1)}\right).\end{align*} $$
$$ \begin{align*}\delta(s)=\prod_{k=1}^{n}s_k^{-(n+1)k(n+1-k)} \ll Y^{-(g^2 + 3g + 1)(n+1) + 55g^4\delta}\left(\prod_{i=1}^{g} s_{g+2+i}^{2i(i+2)(n+1)}\right).\end{align*} $$
Hence,
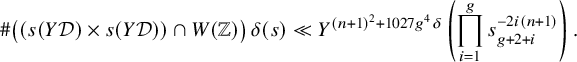 $$ \begin{align} \#\big((s(Y{\mathcal{D}})\times s(Y{\mathcal{D}}))\cap W({\mathbb{Z}})\big)\,\delta(s) \ll Y^{(n+1)^2 + 1027g^4\delta} \left(\prod_{i=1}^{g}s_{g+2+i}^{-2i(n+1)}\right). \end{align} $$
$$ \begin{align} \#\big((s(Y{\mathcal{D}})\times s(Y{\mathcal{D}}))\cap W({\mathbb{Z}})\big)\,\delta(s) \ll Y^{(n+1)^2 + 1027g^4\delta} \left(\prod_{i=1}^{g}s_{g+2+i}^{-2i(n+1)}\right). \end{align} $$
Suppose now
![]() $\#\big ((s(Y{\mathcal {D}})\times s(Y{\mathcal {D}}))\cap W({\mathbb {Z}})\big )\,\delta (s)\gg X^{n+1-\delta }$
. Then, for any
$\#\big ((s(Y{\mathcal {D}})\times s(Y{\mathcal {D}}))\cap W({\mathbb {Z}})\big )\,\delta (s)\gg X^{n+1-\delta }$
. Then, for any
![]() $i = g+3,\ldots ,n$
,
$i = g+3,\ldots ,n$
,
as desired.
Proof of Lemma 6.21.
Suppose
![]() $M>X^\eta $
where
$M>X^\eta $
where
![]() $\eta>0$
is some fixed constant. Suppose
$\eta>0$
is some fixed constant. Suppose
![]() $\delta < \mathrm {{max}}(\eta ,1)/1355g^6$
. Suppose
$\delta < \mathrm {{max}}(\eta ,1)/1355g^6$
. Suppose
![]() ${\mathcal {K}}_1\subset {\mathcal {Z}}$
and
${\mathcal {K}}_1\subset {\mathcal {Z}}$
and
![]() $s\in T_{\mathcal {Z}}(L,Y)$
satisfies (52) and (53). We now impose the conditions
$s\in T_{\mathcal {Z}}(L,Y)$
satisfies (52) and (53). We now impose the conditions
![]() $\det (B) = 0$
and
$\det (B) = 0$
and
![]() $|q|(A,B)>M$
for any
$|q|(A,B)>M$
for any
![]() $(A,B)\in {{\mathcal {L}}(M)} $
to obtain a further saving for
$(A,B)\in {{\mathcal {L}}(M)} $
to obtain a further saving for
![]() $\#\big ((s(Y{\mathcal {D}})\times s(Y{\mathcal {D}}))\cap {{\mathcal {L}}(M)} \big )\,\delta (s)$
.
$\#\big ((s(Y{\mathcal {D}})\times s(Y{\mathcal {D}}))\cap {{\mathcal {L}}(M)} \big )\,\delta (s)$
.
The bound (53) on
![]() $s_{g+3},\ldots ,s_n$
gives
$s_{g+3},\ldots ,s_n$
gives
![]() ${\mathcal {R}}\ll Y^{258g^4\delta }.$
Hence,
${\mathcal {R}}\ll Y^{258g^4\delta }.$
Hence,
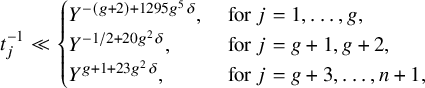 $$ \begin{align} t_j^{-1} \ll\begin{cases} Y^{-(g+2)+1295g^5\delta},&\text{ for }j=1,\ldots,g,\\ Y^{-1/2+ 20g^2\delta},&\text{ for }j=g+1,g+2,\\ Y^{g+1+23g^2\delta},&\text{ for }j = g+3,\ldots,n+1, \end{cases} \end{align} $$
$$ \begin{align} t_j^{-1} \ll\begin{cases} Y^{-(g+2)+1295g^5\delta},&\text{ for }j=1,\ldots,g,\\ Y^{-1/2+ 20g^2\delta},&\text{ for }j=g+1,g+2,\\ Y^{g+1+23g^2\delta},&\text{ for }j = g+3,\ldots,n+1, \end{cases} \end{align} $$
thus improving (62). In this case,
Since
![]() $\delta < 1/(1315g^4)$
, we may assume that every
$\delta < 1/(1315g^4)$
, we may assume that every
![]() $(A,B)\in (s(Y{\mathcal {D}})\times s(Y{\mathcal {D}}))\cap W({\mathbb {Z}})$
satisfies the following:
$(A,B)\in (s(Y{\mathcal {D}})\times s(Y{\mathcal {D}}))\cap W({\mathbb {Z}})$
satisfies the following:
-
(a) The top left
 $g\times (g+2)$
-blocks of A and B are
$g\times (g+2)$
-blocks of A and B are
 $0$
.
$0$
. -
(b) The entries of the top right
 $g\times (g+1)$
blocks of A and B are
$g\times (g+1)$
blocks of A and B are
 $O(Y^{1315g^5\delta })$
.
$O(Y^{1315g^5\delta })$
. -
(c) The entries
 $a_{g+1,g+1}$
,
$a_{g+1,g+1}$
,
 $a_{g+1,g+2}$
,
$a_{g+1,g+2}$
,
 $a_{g+2,g+2}$
,
$a_{g+2,g+2}$
,
 $b_{g+1,g+1}$
,
$b_{g+1,g+1}$
,
 $b_{g+1,g+2}$
, and
$b_{g+1,g+2}$
, and
 $b_{g+2,g+2}$
are
$b_{g+2,g+2}$
are
 $O(Y^{40g^2\delta })$
.
$O(Y^{40g^2\delta })$
. -
(d) The entries
 $a_{g+1,j}$
,
$a_{g+1,j}$
,
 $a_{g+2,j}$
,
$a_{g+2,j}$
,
 $b_{g+1,j}$
and
$b_{g+1,j}$
and
 $b_{g+2,j}$
are
$b_{g+2,j}$
are
 $O(Y^{(n+1)/2+43g^2\delta })$
for
$O(Y^{(n+1)/2+43g^2\delta })$
for
 $g+3\leq j\leq n+1$
.
$g+3\leq j\leq n+1$
. -
(e) The entries
 $a_{ij}$
and
$a_{ij}$
and
 $b_{ij}$
are
$b_{ij}$
are
 $O(Y^{n+1+46g^2\delta })$
for
$O(Y^{n+1+46g^2\delta })$
for
 $g+3\leq i,j\leq n+1$
.
$g+3\leq i,j\leq n+1$
.
Suppose now that
![]() $(A,B)$
is an element of
$(A,B)$
is an element of
![]() $(s(Y{\mathcal {D}})\times s(Y{\mathcal {D}}))\cap {{\mathcal {L}}(M)} $
. Then
$(s(Y{\mathcal {D}})\times s(Y{\mathcal {D}}))\cap {{\mathcal {L}}(M)} $
. Then
![]() $f_{A,B} = xg(x,y)$
, where
$f_{A,B} = xg(x,y)$
, where
![]() $g(x,1)$
is a degree n polynomial with Galois group
$g(x,1)$
is a degree n polynomial with Galois group
![]() $S_n$
.
$S_n$
.
Lemma 6.23. Let
![]() $(A,B)$
be as above. If
$(A,B)$
be as above. If
![]() $b_{g+1,g+1}=b_{g+1,g+2}=b_{g+2,g+2}=0$
, then
$b_{g+1,g+1}=b_{g+1,g+2}=b_{g+2,g+2}=0$
, then
Proof. Since
![]() $(A,B)$
is distinguished over
$(A,B)$
is distinguished over
![]() ${\mathbb {Q}}$
, the set of
${\mathbb {Q}}$
, the set of
![]() $(g+1)$
-dimensional common isotropic subspaces defined over any number field L is in bijection with
$(g+1)$
-dimensional common isotropic subspaces defined over any number field L is in bijection with
![]() $J[2](L)$
, where J is the Jacobian of the hyperelliptic curve
$J[2](L)$
, where J is the Jacobian of the hyperelliptic curve
![]() $y^2 = xg(x,1)$
(which has a rational Weierstrass point at infinity), and
$y^2 = xg(x,1)$
(which has a rational Weierstrass point at infinity), and
![]() $J[2](L)$
is in bijection with the factorizations of
$J[2](L)$
is in bijection with the factorizations of
![]() $xg(x,1)$
over L. Since
$xg(x,1)$
over L. Since
![]() $g(x,1)$
has Galois group
$g(x,1)$
has Galois group
![]() $S_n$
, it does not admit any factorization over any quadratic extension of
$S_n$
, it does not admit any factorization over any quadratic extension of
![]() ${\mathbb {Q}}$
. Therefore, for any quadratic extension K of
${\mathbb {Q}}$
. Therefore, for any quadratic extension K of
![]() ${\mathbb {Q}}$
, we have
${\mathbb {Q}}$
, we have
![]() $J[2](K) = J[2]({\mathbb {Q}})$
, and so any
$J[2](K) = J[2]({\mathbb {Q}})$
, and so any
![]() $(g+1)$
-dimension K-subspace isotropic with respect to A and B admits a
$(g+1)$
-dimension K-subspace isotropic with respect to A and B admits a
![]() ${\mathbb {Q}}$
-basis.
${\mathbb {Q}}$
-basis.
Suppose
![]() $x_0,y_0\in K$
for some quadratic extension K of
$x_0,y_0\in K$
for some quadratic extension K of
![]() ${\mathbb {Q}}$
such that
${\mathbb {Q}}$
such that
![]() $(x_0,y_0)$
is a solution to
$(x_0,y_0)$
is a solution to
By the assumption
![]() $b_{g+1,g+1}=b_{g+1,g+2}=b_{g+2,g+2}=0$
, we see that
$b_{g+1,g+1}=b_{g+1,g+2}=b_{g+2,g+2}=0$
, we see that
is a
![]() $(g+1)$
-dimension K-subspace isotropic with respect to A and B. Let
$(g+1)$
-dimension K-subspace isotropic with respect to A and B. Let
![]() $v_1,\ldots ,v_{g+1}\in {\mathbb {Q}}^{n+1}$
be such that
$v_1,\ldots ,v_{g+1}\in {\mathbb {Q}}^{n+1}$
be such that
We now complete
![]() $\{e_1,\ldots ,e_g\}$
into a
$\{e_1,\ldots ,e_g\}$
into a
![]() ${\mathbb {Q}}$
-basis
${\mathbb {Q}}$
-basis
![]() $\{e_1,\ldots ,e_g,v_0\}$
for
$\{e_1,\ldots ,e_g,v_0\}$
for
![]() $\mathrm {Span}_{\mathbb {Q}}\{v_1,\ldots ,v_{g+1}\}$
. We may use
$\mathrm {Span}_{\mathbb {Q}}\{v_1,\ldots ,v_{g+1}\}$
. We may use
![]() $e_1,\ldots ,e_g$
to clear out the first g coordinates of
$e_1,\ldots ,e_g$
to clear out the first g coordinates of
![]() $v_0$
and take
$v_0$
and take
![]() $v_0$
to be of the form
$v_0$
to be of the form
![]() $x_0'e_{g+1} + y_0'e_{g+2}$
with
$x_0'e_{g+1} + y_0'e_{g+2}$
with
![]() $x_0',y_0'\in {\mathbb {Q}}$
, which implies that
$x_0',y_0'\in {\mathbb {Q}}$
, which implies that
![]() $(x_0',y_0')$
is a nonzero rational solution (65). In particular, the discriminant
$(x_0',y_0')$
is a nonzero rational solution (65). In particular, the discriminant
![]() $a_{g+1,g+2}^2 - 4a_{g+1,g+1}a_{g+2,g+2}\in {\mathbb {Z}}$
is a square.
$a_{g+1,g+2}^2 - 4a_{g+1,g+1}a_{g+2,g+2}\in {\mathbb {Z}}$
is a square.
If
![]() $a_{g+1,g+1}\neq 0$
, let
$a_{g+1,g+1}\neq 0$
, let
If
![]() $a_{g+1,g+1} = 0$
, let
$a_{g+1,g+1} = 0$
, let
![]() $x_1 = 1,\,y_1 = 0$
. Then
$x_1 = 1,\,y_1 = 0$
. Then
![]() $x_1,y_1$
are integers
$x_1,y_1$
are integers
![]() $\ll Y^{40g^2\delta }$
, not both zero, and are solutions to (65). Let
$\ll Y^{40g^2\delta }$
, not both zero, and are solutions to (65). Let
![]() $x_0 = x_1/\gcd (x_1,y_1)$
and
$x_0 = x_1/\gcd (x_1,y_1)$
and
![]() $y_0 = y_1/\gcd (x_1,y_1)$
. There then exist integers
$y_0 = y_1/\gcd (x_1,y_1)$
. There then exist integers
![]() $x_2,y_2\ll Y^{40g^2\delta }$
such that
$x_2,y_2\ll Y^{40g^2\delta }$
such that
forms an integral basis for
![]() ${\mathbb {Z}}^{n+1}$
such that the first
${\mathbb {Z}}^{n+1}$
such that the first
![]() $g+1$
vectors generate a primitive lattice isotropic with respect to A and B, and the first
$g+1$
vectors generate a primitive lattice isotropic with respect to A and B, and the first
![]() $g+2$
vectors generate a primitive lattice isotropic with respect to B. That is, we compute the
$g+2$
vectors generate a primitive lattice isotropic with respect to B. That is, we compute the
![]() $|q|$
-invariant of
$|q|$
-invariant of
![]() $(A,B)$
using this basis. When so expressed, the top right
$(A,B)$
using this basis. When so expressed, the top right
![]() $(g+1)\times (g+2)$
blocks of the Gram matrices of A and B have the form
$(g+1)\times (g+2)$
blocks of the Gram matrices of A and B have the form
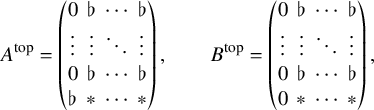 $$ \begin{align*} A^{\mathrm{{top}}} = \begin{pmatrix}0 & \flat & \cdots & \flat\\ \vdots &\vdots &\ddots &\vdots\\ 0 & \flat & \cdots & \flat\\ \flat & * & \cdots & * \end{pmatrix},\qquad B^{\mathrm{{top}}} = \begin{pmatrix} 0 & \flat & \cdots & \flat\\ \vdots &\vdots &\ddots &\vdots\\ 0 & \flat & \cdots & \flat\\ 0 & * & \cdots & * \end{pmatrix}, \end{align*} $$
$$ \begin{align*} A^{\mathrm{{top}}} = \begin{pmatrix}0 & \flat & \cdots & \flat\\ \vdots &\vdots &\ddots &\vdots\\ 0 & \flat & \cdots & \flat\\ \flat & * & \cdots & * \end{pmatrix},\qquad B^{\mathrm{{top}}} = \begin{pmatrix} 0 & \flat & \cdots & \flat\\ \vdots &\vdots &\ddots &\vdots\\ 0 & \flat & \cdots & \flat\\ 0 & * & \cdots & * \end{pmatrix}, \end{align*} $$
where entries labeled ‘
![]() $0$
’ are
$0$
’ are
![]() $0$
, entries labeled ‘
$0$
, entries labeled ‘
![]() $\flat $
’ are
$\flat $
’ are
![]() $O(Y^{1355g^5\delta })$
, and entries labeled ‘
$O(Y^{1355g^5\delta })$
, and entries labeled ‘
![]() $*$
’ are
$*$
’ are
![]() $O(Y^{(n+1)/2 + 83g^2\delta })$
. Let
$O(Y^{(n+1)/2 + 83g^2\delta })$
. Let
![]() $M_1$
denote the
$M_1$
denote the
![]() $(g+2)\times (g+2)$
matrix whose ith row consists of the coefficients of
$(g+2)\times (g+2)$
matrix whose ith row consists of the coefficients of
![]() $\det (A_ix - B_iy)$
, where
$\det (A_ix - B_iy)$
, where
![]() $A_i$
and
$A_i$
and
![]() $B_i$
are the
$B_i$
are the
![]() $(g+1)\times (g+1)$
matrices formed by removing the i-th columns from
$(g+1)\times (g+1)$
matrices formed by removing the i-th columns from
![]() $A^{\mathrm {{top}}}$
and
$A^{\mathrm {{top}}}$
and
![]() $B^{\mathrm {{top}}}$
, respectively. Then
$B^{\mathrm {{top}}}$
, respectively. Then
![]() $M_1$
is of the form
$M_1$
is of the form
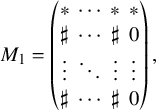 $$ \begin{align*}M_1=\begin{pmatrix} * & \cdots & * & *\\ \sharp & \cdots & \sharp & 0\\ \vdots & \ddots &\vdots & \vdots \\ \sharp & \cdots & \sharp & 0\end{pmatrix}, \end{align*} $$
$$ \begin{align*}M_1=\begin{pmatrix} * & \cdots & * & *\\ \sharp & \cdots & \sharp & 0\\ \vdots & \ddots &\vdots & \vdots \\ \sharp & \cdots & \sharp & 0\end{pmatrix}, \end{align*} $$
where entries labeled ‘
![]() $0$
’ are
$0$
’ are
![]() $0$
, entries labeled ‘
$0$
, entries labeled ‘
![]() $\sharp $
’ are
$\sharp $
’ are
![]() $O(Y^{2710g^6\delta })$
, and entries labeled ‘
$O(Y^{2710g^6\delta })$
, and entries labeled ‘
![]() $*$
’ are
$*$
’ are
![]() $O(Y^{(n+1)/2+1438g^6\delta })$
, where the top right coefficient
$O(Y^{(n+1)/2+1438g^6\delta })$
, where the top right coefficient
![]() $m'$
of
$m'$
of
![]() $M_1$
is the determinant of the top right
$M_1$
is the determinant of the top right
![]() $(g+1)\times (g+1)$
block
$(g+1)\times (g+1)$
block
![]() $B'$
of
$B'$
of
![]() $B^{\mathrm {{top}}}$
, up to sign. Thus,
$B^{\mathrm {{top}}}$
, up to sign. Thus,
where
![]() $M_1'$
is the bottom left
$M_1'$
is the bottom left
![]() $(g+1)\times (g+1)$
block of
$(g+1)\times (g+1)$
block of
![]() $M_1$
. Since the coefficients of
$M_1$
. Since the coefficients of
![]() $M_1'$
are
$M_1'$
are
![]() $\ll Y^{2710g^6\delta }$
, it follows that
$\ll Y^{2710g^6\delta }$
, it follows that
![]() $|q|(A,B)\ll X^{2710g^6(g+1)\delta /(n+1)} \ll X^{1355g^6\delta }$
.
$|q|(A,B)\ll X^{2710g^6(g+1)\delta /(n+1)} \ll X^{1355g^6\delta }$
.
We now return to the proof of Lemma 6.21. For any
![]() $(A,B)\in (s(Y{\mathcal {D}})\times s(Y{\mathcal {D}}))\cap {{\mathcal {L}}(M)} $
, since
$(A,B)\in (s(Y{\mathcal {D}})\times s(Y{\mathcal {D}}))\cap {{\mathcal {L}}(M)} $
, since
![]() $|q|(A,B)> M > X^\eta $
, we may assume that
$|q|(A,B)> M > X^\eta $
, we may assume that
![]() $b_{g+1,g+1}$
,
$b_{g+1,g+1}$
,
![]() $b_{g+1,g+2}$
, and
$b_{g+1,g+2}$
, and
![]() $b_{g+2,g+2}$
are not all
$b_{g+2,g+2}$
are not all
![]() $0$
since
$0$
since
![]() $\delta < \eta /(1355g^6)$
.
$\delta < \eta /(1355g^6)$
.
We now fix
![]() $b_{ij}$
for
$b_{ij}$
for
![]() $1\leq i\leq g, g+3\leq j\leq n+1$
, and
$1\leq i\leq g, g+3\leq j\leq n+1$
, and
![]() $i = g+1,g+2$
,
$i = g+1,g+2$
,
![]() $j=g+1,g+2$
. We consider the number of pairs
$j=g+1,g+2$
. We consider the number of pairs
![]() $(A,B)\in (s(Y{\mathcal {D}})\times s(Y{\mathcal {D}}))\cap {{\mathcal {L}}(M)} $
with these prescribed coefficients by viewing
$(A,B)\in (s(Y{\mathcal {D}})\times s(Y{\mathcal {D}}))\cap {{\mathcal {L}}(M)} $
with these prescribed coefficients by viewing
![]() $\det (B)$
as a polynomial F in
$\det (B)$
as a polynomial F in
![]() $b_{ij}$
for
$b_{ij}$
for
![]() $g+1\leq i\leq n+1$
and
$g+1\leq i\leq n+1$
and
![]() $g+3\leq j\leq n+1$
. Note that all of these remaining coefficients have range at least
$g+3\leq j\leq n+1$
. Note that all of these remaining coefficients have range at least
 $$ \begin{align*}Y^{(n+1)/2 + 43g^2\delta}\prod_{i=g+3}^n s_i^{-(n+1)}.\end{align*} $$
$$ \begin{align*}Y^{(n+1)/2 + 43g^2\delta}\prod_{i=g+3}^n s_i^{-(n+1)}.\end{align*} $$
Hence, to complete the proof of Lemma 6.21, it remains to prove that F is a nonzero polynomial, for then we would have, using (63), that
 $$ \begin{align*} \#\big((s(Y{\mathcal{D}})\times s(Y{\mathcal{D}}))\cap {{\mathcal{L}}(M)} \big)\,\delta(s) &\ll Y^{(n+1)^2 + 1027g^4\delta - (n+1)/2 - 43g^2\delta}\, \prod_{i=1}^{g}s_{g+2+i}^{-(2i-1)(n+1)}\\ &\ll X^{n+1+514g^3\delta - 1/2}. \end{align*} $$
$$ \begin{align*} \#\big((s(Y{\mathcal{D}})\times s(Y{\mathcal{D}}))\cap {{\mathcal{L}}(M)} \big)\,\delta(s) &\ll Y^{(n+1)^2 + 1027g^4\delta - (n+1)/2 - 43g^2\delta}\, \prod_{i=1}^{g}s_{g+2+i}^{-(2i-1)(n+1)}\\ &\ll X^{n+1+514g^3\delta - 1/2}. \end{align*} $$
We may assume that the top right
![]() $g\times (g+1)$
block of B has full rank, for otherwise the kernel of B would be isotropic with respect to A forcing
$g\times (g+1)$
block of B has full rank, for otherwise the kernel of B would be isotropic with respect to A forcing
![]() $\Delta (A,B) = 0$
by Lemma 6.4. Hence, we may also assume that the top right
$\Delta (A,B) = 0$
by Lemma 6.4. Hence, we may also assume that the top right
![]() $g\times (g+1)$
block of B equals
$g\times (g+1)$
block of B equals
![]() $(I_g\,\, 0)$
, where
$(I_g\,\, 0)$
, where
![]() $I_g$
denotes the
$I_g$
denotes the
![]() $g\times g$
identity matrix. Then
$g\times g$
identity matrix. Then
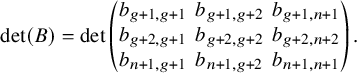 $$ \begin{align*}\det(B) = \det\begin{pmatrix} b_{g+1,g+1}& b_{g+1,g+2} & b_{g+1,n+1}\\ b_{g+2,g+1} & b_{g+2,g+2} & b_{g+2,n+2} \\ b_{n+1,g+1} & b_{n+1,g+2} & b_{n+1,n+1}\end{pmatrix}.\end{align*} $$
$$ \begin{align*}\det(B) = \det\begin{pmatrix} b_{g+1,g+1}& b_{g+1,g+2} & b_{g+1,n+1}\\ b_{g+2,g+1} & b_{g+2,g+2} & b_{g+2,n+2} \\ b_{n+1,g+1} & b_{n+1,g+2} & b_{n+1,n+1}\end{pmatrix}.\end{align*} $$
Since
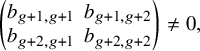 $$ \begin{align*}\begin{pmatrix} b_{g+1,g+1}& b_{g+1,g+2}\\b_{g+2,g+1} & b_{g+2,g+2}\end{pmatrix}\neq 0,\end{align*} $$
$$ \begin{align*}\begin{pmatrix} b_{g+1,g+1}& b_{g+1,g+2}\\b_{g+2,g+1} & b_{g+2,g+2}\end{pmatrix}\neq 0,\end{align*} $$
we see that
![]() $\det (B)$
is a nonzero polynomial in
$\det (B)$
is a nonzero polynomial in
![]() $b_{g+1,n+1}$
,
$b_{g+1,n+1}$
,
![]() $b_{g+2,n+1}$
, and
$b_{g+2,n+1}$
, and
![]() $b_{n+1,n+1}$
.
$b_{n+1,n+1}$
.
6.4 Bounding the number of distinguished elements in the deep cusp
In this subsection, we bound the number of elements with large q-invariant that lie in the deep cusp.
Theorem 6.24. We have
![]() $ {\mathcal {I}}_X^{\mathrm {{dcusp}}}({{\mathcal {L}}(M)} )=O\Big (\frac {X^{n+1+\frac 12\kappa }}{M}\log ^{2n}X\Big ). $
$ {\mathcal {I}}_X^{\mathrm {{dcusp}}}({{\mathcal {L}}(M)} )=O\Big (\frac {X^{n+1+\frac 12\kappa }}{M}\log ^{2n}X\Big ). $
Recall from (40) that
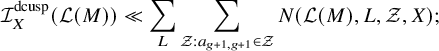 $$ \begin{align*} {\mathcal{I}}_X^{\mathrm{{dcusp}}}({{\mathcal{L}}(M)} )\ll \sum_L\sum_{{\mathcal{Z}}:a_{g+1,g+1}\in{\mathcal{Z}}}N({{\mathcal{L}}(M)} ,L,{\mathcal{Z}},X); \end{align*} $$
$$ \begin{align*} {\mathcal{I}}_X^{\mathrm{{dcusp}}}({{\mathcal{L}}(M)} )\ll \sum_L\sum_{{\mathcal{Z}}:a_{g+1,g+1}\in{\mathcal{Z}}}N({{\mathcal{L}}(M)} ,L,{\mathcal{Z}},X); \end{align*} $$
here, the first sum is over r-tuples
![]() $L=(L_1,\ldots ,L_r)$
with
$L=(L_1,\ldots ,L_r)$
with
![]() $L_1\leq L_2\leq \cdots \leq L_n$
that partition the region
$L_1\leq L_2\leq \cdots \leq L_n$
that partition the region
![]() $\{(\mu _1,\ldots ,\mu _r)\in [Y^{-\Theta _1},Y^{\Theta _2}]^r:\mu _1\leq \ldots \leq \mu _r\}$
into dyadic ranges, and the second sum is over saturated subsets
$\{(\mu _1,\ldots ,\mu _r)\in [Y^{-\Theta _1},Y^{\Theta _2}]^r:\mu _1\leq \ldots \leq \mu _r\}$
into dyadic ranges, and the second sum is over saturated subsets
![]() ${\mathcal {Z}}$
of
${\mathcal {Z}}$
of
![]() ${\mathcal {K}}\cup {\mathcal {M}}$
, where
${\mathcal {K}}\cup {\mathcal {M}}$
, where
The set
![]() ${\mathcal {S}}(L,s)$
is the union over
${\mathcal {S}}(L,s)$
is the union over
![]() $\Lambda \in \Sigma (L,s)$
of
$\Lambda \in \Sigma (L,s)$
of
![]() $S(\Lambda )$
, where
$S(\Lambda )$
, where
![]() $S(\Lambda )$
denotes the lattice of integral symmetric matrices whose row space is contained in
$S(\Lambda )$
denotes the lattice of integral symmetric matrices whose row space is contained in
![]() $\Lambda \otimes {\mathbb {R}}$
, and
$\Lambda \otimes {\mathbb {R}}$
, and
![]() $\Sigma (L,s)$
denotes the set of primitive lattices
$\Sigma (L,s)$
denotes the set of primitive lattices
![]() $\Lambda \in {\mathbb {Z}}^{n+1}$
of rank n such that the successive minima
$\Lambda \in {\mathbb {Z}}^{n+1}$
of rank n such that the successive minima
![]() $\mu _1,\ldots ,\mu _n$
of
$\mu _1,\ldots ,\mu _n$
of
![]() $s^{-1}(\Lambda )$
satisfy
$s^{-1}(\Lambda )$
satisfy
![]() $L_i\leq \mu _i<2L_i$
for each
$L_i\leq \mu _i<2L_i$
for each
![]() $i\in \{1,\ldots ,n\}$
. Finally, recall from §6.1 and Proposition 5.4 that
$i\in \{1,\ldots ,n\}$
. Finally, recall from §6.1 and Proposition 5.4 that
for every
![]() $s\in T_{\mathcal {Z}}(Y,L)$
. Hence, we may assume that
$s\in T_{\mathcal {Z}}(Y,L)$
. Hence, we may assume that
![]() $\ell _{g+1,g+1}\in {\mathcal {Z}}$
.
$\ell _{g+1,g+1}\in {\mathcal {Z}}$
.
The deep cusp contains
![]() $\asymp X^{n+1}$
elements, and we obtain a saving because the elements we are counting have q-invariant greater than M. To make use of this condition, we require an upper bound on the size of the
$\asymp X^{n+1}$
elements, and we obtain a saving because the elements we are counting have q-invariant greater than M. To make use of this condition, we require an upper bound on the size of the
![]() $|q|$
-invariant of elements in
$|q|$
-invariant of elements in
![]() $(s(Y{\mathcal {D}})\times s(Y{\mathcal {D}})) \cap {{\mathcal {L}}(1)} $
. To accomplish this, we have the following preliminary result.
$(s(Y{\mathcal {D}})\times s(Y{\mathcal {D}})) \cap {{\mathcal {L}}(1)} $
. To accomplish this, we have the following preliminary result.
Lemma 6.25. Let
![]() $(A,B)\in (Y{\mathcal {D}}\times Y{\mathcal {D}})\cap W_{0}({\mathbb {R}})$
be such that
$(A,B)\in (Y{\mathcal {D}}\times Y{\mathcal {D}})\cap W_{0}({\mathbb {R}})$
be such that
![]() $\Delta (A,B)> X^{2n-2-\kappa }$
. Denote the top right
$\Delta (A,B)> X^{2n-2-\kappa }$
. Denote the top right
![]() $(g+1)\times (g+2)$
block of B by
$(g+1)\times (g+2)$
block of B by
![]() $B^{\mathrm {{top}}}$
. Then
$B^{\mathrm {{top}}}$
. Then
Proof. Let
![]() $(A',B')=Y^{-1}(A,B)\in ({\mathcal {D}}\times {\mathcal {D}})\cap W_{0}({\mathbb {R}})$
. Then it suffices to prove that
$(A',B')=Y^{-1}(A,B)\in ({\mathcal {D}}\times {\mathcal {D}})\cap W_{0}({\mathbb {R}})$
. Then it suffices to prove that
Since
![]() $|\Delta (A,B)|>X^{2n-2-\kappa }$
, we have
$|\Delta (A,B)|>X^{2n-2-\kappa }$
, we have
![]() $|\Delta (A',B')|>X^{-\kappa }$
. By Proposition 3.6, there is a polynomial
$|\Delta (A',B')|>X^{-\kappa }$
. By Proposition 3.6, there is a polynomial
![]() $P\in {\mathbb {Z}}[W_{0}]$
such that
$P\in {\mathbb {Z}}[W_{0}]$
such that
for any
![]() $(A",B")\in W_{0}({\mathbb {R}})$
. Since
$(A",B")\in W_{0}({\mathbb {R}})$
. Since
![]() $(A',B')\in {\mathcal {D}}\times {\mathcal {D}}$
, which is an absolutely bounded region, we have
$(A',B')\in {\mathcal {D}}\times {\mathcal {D}}$
, which is an absolutely bounded region, we have
![]() $|P(A',B')|\ll 1$
. Hence,
$|P(A',B')|\ll 1$
. Hence,
as desired.
Next, we have the following upper bound on the
![]() $|q|$
-invariant.
$|q|$
-invariant.
Proposition 6.26. Let
![]() ${\mathcal {Z}}\subset {\mathcal {Z}}_1$
be a saturated set containing
${\mathcal {Z}}\subset {\mathcal {Z}}_1$
be a saturated set containing
![]() $a_{g+1,g+1}$
and
$a_{g+1,g+1}$
and
![]() $\ell _{g+1,g+1}$
. Let
$\ell _{g+1,g+1}$
. Let
![]() $L=(L_1,\ldots ,L_n)$
be a sequence of nondecreasing positive real numbers. Then for any
$L=(L_1,\ldots ,L_n)$
be a sequence of nondecreasing positive real numbers. Then for any
![]() $s\in T_{\mathcal {Z}}(L,Y)$
and
$s\in T_{\mathcal {Z}}(L,Y)$
and
![]() $(A,B)\in (s(Y{\mathcal {D}})\times s(Y{\mathcal {D}}))\cap {{\mathcal {L}}(1)} $
, we have
$(A,B)\in (s(Y{\mathcal {D}})\times s(Y{\mathcal {D}}))\cap {{\mathcal {L}}(1)} $
, we have
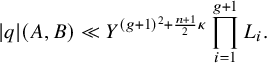 $$ \begin{align} |q|(A,B) \ll Y^{(g+1)^2+\frac{n+1}{2}\kappa}\prod_{i=1}^{g+1} L_i. \end{align} $$
$$ \begin{align} |q|(A,B) \ll Y^{(g+1)^2+\frac{n+1}{2}\kappa}\prod_{i=1}^{g+1} L_i. \end{align} $$
Proof. Suppose
![]() $(A,B)\in (s(Y{\mathcal {D}})\times s(Y{\mathcal {D}}))\cap {{\mathcal {L}}(1)} $
. Since
$(A,B)\in (s(Y{\mathcal {D}})\times s(Y{\mathcal {D}}))\cap {{\mathcal {L}}(1)} $
. Since
![]() $a_{g+1,g+1}\in {\mathcal {Z}}$
, we have
$a_{g+1,g+1}\in {\mathcal {Z}}$
, we have
![]() $(A,B)\in W_{0}({\mathbb {Z}})$
. By Lemma 6.4,
$(A,B)\in W_{0}({\mathbb {Z}})$
. By Lemma 6.4,
![]() $\ker (B)$
is
$\ker (B)$
is
![]() $1$
-dimensional and does not lie inside
$1$
-dimensional and does not lie inside
![]() $\text {Span}\{e_1,\ldots ,e_{g+1}\}$
as this
$\text {Span}\{e_1,\ldots ,e_{g+1}\}$
as this
![]() $(g+1)$
-plane is isotropic with respect to A. Let
$(g+1)$
-plane is isotropic with respect to A. Let
![]() $w_1\in \text {Span}_{\mathbb {Z}}\{e_{g+2},\ldots ,e_{n+1}\}$
be a primitive vector so that
$w_1\in \text {Span}_{\mathbb {Z}}\{e_{g+2},\ldots ,e_{n+1}\}$
be a primitive vector so that
![]() $\{e_1,\ldots ,e_{g+1},w_1\}$
forms a basis for the primitive lattice in
$\{e_1,\ldots ,e_{g+1},w_1\}$
forms a basis for the primitive lattice in
![]() $\text {Span}_{\mathbb {R}}\{e_1,\ldots ,e_{g+1}\} + \ker (B).$
Complete
$\text {Span}_{\mathbb {R}}\{e_1,\ldots ,e_{g+1}\} + \ker (B).$
Complete
![]() $w_1$
to an integral basis
$w_1$
to an integral basis
![]() $\{w_1,\ldots ,w_{g+2}\}$
for
$\{w_1,\ldots ,w_{g+2}\}$
for
![]() $\text {Span}_{\mathbb {Z}}\{e_{g+2},\ldots ,e_{n+1}\}$
. We can now use the integral basis
$\text {Span}_{\mathbb {Z}}\{e_{g+2},\ldots ,e_{n+1}\}$
. We can now use the integral basis
of
![]() ${\mathbb {Z}}^{n+1}$
to compute the
${\mathbb {Z}}^{n+1}$
to compute the
![]() $|q|$
-invariant of
$|q|$
-invariant of
![]() $(A,B)$
, as the first
$(A,B)$
, as the first
![]() $g+1$
vectors generate a primitive lattice isotropic with respect to A and B, and the first
$g+1$
vectors generate a primitive lattice isotropic with respect to A and B, and the first
![]() $g+2$
vectors generate a primitive lattice isotropic with respect to B. Note also that with respect to the standard inner product on
$g+2$
vectors generate a primitive lattice isotropic with respect to B. Note also that with respect to the standard inner product on
![]() ${\mathbb {R}}^{n+1}$
, since
${\mathbb {R}}^{n+1}$
, since
![]() $w_1\in \text {Span}_{\mathbb {R}}\{e_1,\ldots ,e_{g+1}\} + \ker (B)$
, we have
$w_1\in \text {Span}_{\mathbb {R}}\{e_1,\ldots ,e_{g+1}\} + \ker (B)$
, we have
where
![]() $C(B)$
denotes the column space of B.
$C(B)$
denotes the column space of B.
Let
![]() $A'$
and
$A'$
and
![]() $B'$
be the Gram matrices of the quadratic forms defined by A and B with respect to this new basis (67). Since the first
$B'$
be the Gram matrices of the quadratic forms defined by A and B with respect to this new basis (67). Since the first
![]() $g+1$
vectors of this basis are part of the standard basis, we see that
$g+1$
vectors of this basis are part of the standard basis, we see that
![]() $(A,B)$
and
$(A,B)$
and
![]() $(A',B')$
are
$(A',B')$
are
![]() $G_0({\mathbb {Z}})$
-equivalent, where
$G_0({\mathbb {Z}})$
-equivalent, where
![]() $G_0$
is defined in §3.1. Hence,
$G_0$
is defined in §3.1. Hence,
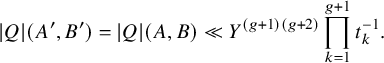 $$ \begin{align*} |Q|(A',B') = |Q|(A,B) \ll Y^{(g+1)(g+2)}\prod_{k=1}^{g+1} t_k^{-1}. \end{align*} $$
$$ \begin{align*} |Q|(A',B') = |Q|(A,B) \ll Y^{(g+1)(g+2)}\prod_{k=1}^{g+1} t_k^{-1}. \end{align*} $$
Let
![]() $B"$
denote the top right
$B"$
denote the top right
![]() $(g+1)\times (g+1)$
block of
$(g+1)\times (g+1)$
block of
![]() $B'$
. Then, by the definition of q, we have
$B'$
. Then, by the definition of q, we have
 $$ \begin{align} |q|(A,B) = |q|(A',B') = \frac{|Q|(A',B')}{|\det(B")|} \ll \frac{1}{|\det(B")|}Y^{(g+1)(g+2)}\prod_{k=1}^{g+1} t_k^{-1}. \end{align} $$
$$ \begin{align} |q|(A,B) = |q|(A',B') = \frac{|Q|(A',B')}{|\det(B")|} \ll \frac{1}{|\det(B")|}Y^{(g+1)(g+2)}\prod_{k=1}^{g+1} t_k^{-1}. \end{align} $$
We now work towards proving a lower bound on
![]() $|\det (B")|$
. Let
$|\det (B")|$
. Let
![]() $p_1$
(resp.,
$p_1$
(resp.,
![]() $p_2$
) denote the projection of
$p_2$
) denote the projection of
![]() ${\mathbb {R}}^{n+1}$
onto the first
${\mathbb {R}}^{n+1}$
onto the first
![]() $g+1$
coefficients (resp., the last
$g+1$
coefficients (resp., the last
![]() $g+2$
coefficients). Let
$g+2$
coefficients). Let
![]() $B^{\mathrm {{top}}}$
(resp.,
$B^{\mathrm {{top}}}$
(resp.,
![]() $B^{\prime \mathrm {{top}}}$
) denote the top right
$B^{\prime \mathrm {{top}}}$
) denote the top right
![]() $(g+1)\times (g+2)$
block of B (resp.,
$(g+1)\times (g+2)$
block of B (resp.,
![]() $B'$
). Then by (68), we have
$B'$
). Then by (68), we have
![]() $B^{\mathrm {{top}}} p_2(w_1) = 0$
. Consider the following two
$B^{\mathrm {{top}}} p_2(w_1) = 0$
. Consider the following two
![]() $(g+2)\times (g+2)$
matrices in block form:
$(g+2)\times (g+2)$
matrices in block form:
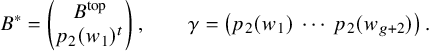 $$ \begin{align*}B^* = \begin{pmatrix}B^{\mathrm{{top}}}\\ p_2(w_1)^t\end{pmatrix},\qquad \gamma = \begin{pmatrix}p_2(w_1)&\cdots&p_2(w_{g+2})\end{pmatrix}. \end{align*} $$
$$ \begin{align*}B^* = \begin{pmatrix}B^{\mathrm{{top}}}\\ p_2(w_1)^t\end{pmatrix},\qquad \gamma = \begin{pmatrix}p_2(w_1)&\cdots&p_2(w_{g+2})\end{pmatrix}. \end{align*} $$
Then
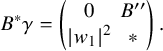 $$ \begin{align*} B^*\gamma = \begin{pmatrix}0&B"\\ |w_1|^2&*\end{pmatrix}. \end{align*} $$
$$ \begin{align*} B^*\gamma = \begin{pmatrix}0&B"\\ |w_1|^2&*\end{pmatrix}. \end{align*} $$
Let
![]() $\Lambda _2$
denote the rank
$\Lambda _2$
denote the rank
![]() $g+1$
lattice in
$g+1$
lattice in
![]() ${\mathbb {Z}}^{g+2}$
spanned by the rows of
${\mathbb {Z}}^{g+2}$
spanned by the rows of
![]() $B^{\mathrm {{top}}}$
. Then
$B^{\mathrm {{top}}}$
. Then
![]() $|\det (B^*)| = d(\Lambda _2)|w_1|.$
Since
$|\det (B^*)| = d(\Lambda _2)|w_1|.$
Since
![]() $\{p_2(w_1),\ldots ,p_2(w_{g+2})\}$
is an integral basis for
$\{p_2(w_1),\ldots ,p_2(w_{g+2})\}$
is an integral basis for
![]() ${\mathbb {Z}}^{g+2}$
, we have
${\mathbb {Z}}^{g+2}$
, we have
![]() $\det \gamma = \pm 1$
, and so
$\det \gamma = \pm 1$
, and so
We now use the fact that
![]() $B\in {\mathcal {S}}(L,s)$
. This means that the row span of B lies in an n-dimensional primitive lattice
$B\in {\mathcal {S}}(L,s)$
. This means that the row span of B lies in an n-dimensional primitive lattice
![]() $\Lambda \subset {\mathbb {Z}}^{n+1}$
with basis of the form
$\Lambda \subset {\mathbb {Z}}^{n+1}$
with basis of the form
![]() $\{s\ell _1,\ldots ,s\ell _n\}$
where
$\{s\ell _1,\ldots ,s\ell _n\}$
where
![]() $L_i\leq |\ell _i|<2L_i$
and
$L_i\leq |\ell _i|<2L_i$
and
![]() $\{\ell _1,\ldots ,\ell _n\}$
are reduced. By assumption,
$\{\ell _1,\ldots ,\ell _n\}$
are reduced. By assumption,
![]() $\ell _{g+1,g+1}\in {\mathcal {Z}}$
, and hence,
$\ell _{g+1,g+1}\in {\mathcal {Z}}$
, and hence,
![]() $\ell _{i,j}\in {\mathcal {Z}}$
for all
$\ell _{i,j}\in {\mathcal {Z}}$
for all
![]() $i\leq g+1$
and
$i\leq g+1$
and
![]() $j\leq g+1$
. Thus, the first
$j\leq g+1$
. Thus, the first
![]() $g+1$
coefficients of
$g+1$
coefficients of
![]() $s\ell _1,\ldots ,s\ell _{g+1}$
are all
$s\ell _1,\ldots ,s\ell _{g+1}$
are all
![]() $0$
, and
$0$
, and
![]() $\{s\ell _1,\ldots ,s\ell _{g+1}\}$
forms an integral basis of a primitive lattice
$\{s\ell _1,\ldots ,s\ell _{g+1}\}$
forms an integral basis of a primitive lattice
![]() $\Lambda _1$
of rank
$\Lambda _1$
of rank
![]() $g+1$
in
$g+1$
in
![]() $\text {Span}_{\mathbb {R}}\{e_{g+2},\ldots ,e_{n+1}\}$
. By (68),
$\text {Span}_{\mathbb {R}}\{e_{g+2},\ldots ,e_{n+1}\}$
. By (68),
![]() $w_1$
is a primitive vector in
$w_1$
is a primitive vector in
![]() $\text {Span}_{\mathbb {R}}\{e_{g+2},\ldots ,e_{n+1}\}$
orthogonal to
$\text {Span}_{\mathbb {R}}\{e_{g+2},\ldots ,e_{n+1}\}$
orthogonal to
![]() $\Lambda _1$
. Hence,
$\Lambda _1$
. Hence,
By (68), we have
![]() $\text {Span}_{\mathbb {R}}\{e_{g+2},\ldots ,e_{n+1}\}\cap C(B)\neq \text {Span}_{\mathbb {R}}\{e_{g+2},\ldots ,e_{n+1}\}$
, and so
$\text {Span}_{\mathbb {R}}\{e_{g+2},\ldots ,e_{n+1}\}\cap C(B)\neq \text {Span}_{\mathbb {R}}\{e_{g+2},\ldots ,e_{n+1}\}$
, and so
In particular, since
![]() $\Lambda _1$
is primitive, the first
$\Lambda _1$
is primitive, the first
![]() $g+1$
columns of B belong to
$g+1$
columns of B belong to
![]() $\Lambda _1$
. That is, there is a
$\Lambda _1$
. That is, there is a
![]() $(g+1)\times (g+1)$
matrix C (with integer coefficients) such that
$(g+1)\times (g+1)$
matrix C (with integer coefficients) such that
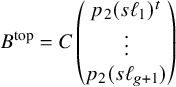 $$ \begin{align*} B^{\mathrm{{top}}} = C\begin{pmatrix}p_2(s\ell_1)^t\\ \vdots\\ p_2(s\ell_{g+1})\end{pmatrix} \end{align*} $$
$$ \begin{align*} B^{\mathrm{{top}}} = C\begin{pmatrix}p_2(s\ell_1)^t\\ \vdots\\ p_2(s\ell_{g+1})\end{pmatrix} \end{align*} $$
and so
To obtain a lower bound on
![]() $|\det (C)|$
, we write
$|\det (C)|$
, we write
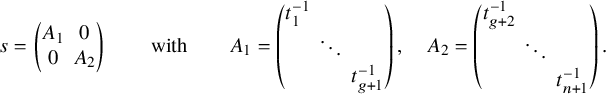 $$ \begin{align*} s = \begin{pmatrix} A_1&0\\0&A_2\end{pmatrix} \qquad \text{with} \qquad A_1 = \begin{pmatrix}t_1^{-1}& &\\ &\ddots&\\&&t_{g+1}^{-1}\end{pmatrix}, \quad A_2 = \begin{pmatrix} t_{g+2}^{-1}& &\\ &\ddots&\\&&t_{n+1}^{-1}\end{pmatrix}. \end{align*} $$
$$ \begin{align*} s = \begin{pmatrix} A_1&0\\0&A_2\end{pmatrix} \qquad \text{with} \qquad A_1 = \begin{pmatrix}t_1^{-1}& &\\ &\ddots&\\&&t_{g+1}^{-1}\end{pmatrix}, \quad A_2 = \begin{pmatrix} t_{g+2}^{-1}& &\\ &\ddots&\\&&t_{n+1}^{-1}\end{pmatrix}. \end{align*} $$
Let
![]() $M^{\mathrm {{top}}}$
denote the
$M^{\mathrm {{top}}}$
denote the
![]() $(g+1)\times (g+2)$
matrix with rows
$(g+1)\times (g+2)$
matrix with rows
![]() $p_2(\ell _1)^t,\ldots ,p_2(\ell _{g+1})^t$
. Then
$p_2(\ell _1)^t,\ldots ,p_2(\ell _{g+1})^t$
. Then
Consider the pair
![]() $(A_0,B_0):=s^{-1}(A,B)\in (Y{\mathcal {D}}\times Y{\mathcal {D}})\cap W_{0,n+1}({\mathbb {R}})$
satisfying
$(A_0,B_0):=s^{-1}(A,B)\in (Y{\mathcal {D}}\times Y{\mathcal {D}})\cap W_{0,n+1}({\mathbb {R}})$
satisfying
since
![]() $(A,B)\in {{\mathcal {L}}(1)} $
. The top right
$(A,B)\in {{\mathcal {L}}(1)} $
. The top right
![]() $(g+1)\times (g+2)$
block
$(g+1)\times (g+2)$
block
![]() $B_{0}^{\mathrm {{top}}}$
of
$B_{0}^{\mathrm {{top}}}$
of
![]() $B_0$
satisfies
$B_0$
satisfies
and so
The rows of
![]() $M^{\mathrm {{top}}}$
form a reduced basis for a lattice
$M^{\mathrm {{top}}}$
form a reduced basis for a lattice
![]() $\Lambda _3\subset {\mathbb {Z}}^{g+2}$
with
$\Lambda _3\subset {\mathbb {Z}}^{g+2}$
with
![]() $L_i\leq |p_2(\ell _i)|<2L_i$
. Thus,
$L_i\leq |p_2(\ell _i)|<2L_i$
. Thus,
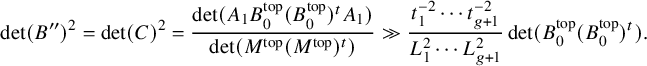 $$ \begin{align} \det(B")^2=\det(C)^2= \frac{\det(A_1B_{0}^{\mathrm{{top}}} (B_{0}^{\mathrm{{top}}})^tA_1)}{\det(M^{\mathrm{{top}}} (M^{\mathrm{{top}}})^t)}\gg \frac{t_1^{-2}\cdots t_{g+1}^{-2}}{L_1^2\cdots L_{g+1}^2} \det(B_{0}^{\mathrm{{top}}} (B_{0}^{\mathrm{{top}}})^t). \end{align} $$
$$ \begin{align} \det(B")^2=\det(C)^2= \frac{\det(A_1B_{0}^{\mathrm{{top}}} (B_{0}^{\mathrm{{top}}})^tA_1)}{\det(M^{\mathrm{{top}}} (M^{\mathrm{{top}}})^t)}\gg \frac{t_1^{-2}\cdots t_{g+1}^{-2}}{L_1^2\cdots L_{g+1}^2} \det(B_{0}^{\mathrm{{top}}} (B_{0}^{\mathrm{{top}}})^t). \end{align} $$
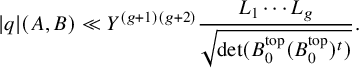 $$ \begin{align*} |q|(A,B)\ll Y^{(g+1)(g+2)} \frac{L_1\cdots L_g}{\sqrt{\det(B_{0}^{\mathrm{{top}}} (B_{0}^{\mathrm{{top}}})^t)}}. \end{align*} $$
$$ \begin{align*} |q|(A,B)\ll Y^{(g+1)(g+2)} \frac{L_1\cdots L_g}{\sqrt{\det(B_{0}^{\mathrm{{top}}} (B_{0}^{\mathrm{{top}}})^t)}}. \end{align*} $$
The result now follows from Lemma 6.25.
Proof of Theorem 6.24.
We write
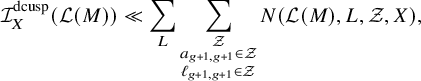 $$ \begin{align} {\mathcal{I}}_X^{\mathrm{{dcusp}}}({{\mathcal{L}}(M)} )\ll \sum_{L} \sum_{\substack{{\mathcal{Z}}\\a_{g+1,g+1}\in{\mathcal{Z}}\\\ell_{g+1,g+1}\in{\mathcal{Z}}}} N({{\mathcal{L}}(M)} ,L,{\mathcal{Z}},X), \end{align} $$
$$ \begin{align} {\mathcal{I}}_X^{\mathrm{{dcusp}}}({{\mathcal{L}}(M)} )\ll \sum_{L} \sum_{\substack{{\mathcal{Z}}\\a_{g+1,g+1}\in{\mathcal{Z}}\\\ell_{g+1,g+1}\in{\mathcal{Z}}}} N({{\mathcal{L}}(M)} ,L,{\mathcal{Z}},X), \end{align} $$
and obtain upper bounds on
![]() $N({{\mathcal {L}}(M)} ,L,{\mathcal {Z}},X)$
for each
$N({{\mathcal {L}}(M)} ,L,{\mathcal {Z}},X)$
for each
![]() ${\mathcal {Z}}\subset {\mathcal {Z}}_1$
with
${\mathcal {Z}}\subset {\mathcal {Z}}_1$
with
![]() $a_{g+1,g+1},\ell _{g+1,g+1}\in {\mathcal {Z}}$
. Fix such a set
$a_{g+1,g+1},\ell _{g+1,g+1}\in {\mathcal {Z}}$
. Fix such a set
![]() ${\mathcal {Z}}$
with
${\mathcal {Z}}$
with
![]() $N({{\mathcal {L}}(M)} ,L,{\mathcal {Z}},X)>0$
and an element
$N({{\mathcal {L}}(M)} ,L,{\mathcal {Z}},X)>0$
and an element
![]() $s\in T_{\mathcal {Z}}(L,Y)$
. Then
$s\in T_{\mathcal {Z}}(L,Y)$
. Then
We begin by bounding the number of elements in
![]() $\#(s(Y{\mathcal {D}})\cap S({\mathbb {Z}}))$
. Let
$\#(s(Y{\mathcal {D}})\cap S({\mathbb {Z}}))$
. Let
![]() ${\mathcal {K}}_{\mathrm {{dist}}} := \{a_{ij}\mid 1\leq i\leq j\leq g+1\}$
. By assumption,
${\mathcal {K}}_{\mathrm {{dist}}} := \{a_{ij}\mid 1\leq i\leq j\leq g+1\}$
. By assumption,
![]() ${\mathcal {K}}_{\mathrm {{dist}}}$
is a subset of
${\mathcal {K}}_{\mathrm {{dist}}}$
is a subset of
![]() ${\mathcal {Z}}\cap {\mathcal {K}}$
. Define
${\mathcal {Z}}\cap {\mathcal {K}}$
. Define
![]() $\pi _{\mathcal {K}}: {\mathcal {Z}}_1\cap {\mathcal {K}}\rightarrow {\mathcal {K}}\backslash {\mathcal {Z}}_1$
by
$\pi _{\mathcal {K}}: {\mathcal {Z}}_1\cap {\mathcal {K}}\rightarrow {\mathcal {K}}\backslash {\mathcal {Z}}_1$
by
This agrees with the
![]() $\pi _k$
as defined in §6.3.1 when restricted to
$\pi _k$
as defined in §6.3.1 when restricted to
![]() ${\mathcal {K}}$
. For any
${\mathcal {K}}$
. For any
![]() $\alpha \in {\mathcal {Z}}_1\cap {\mathcal {K}}$
, we have
$\alpha \in {\mathcal {Z}}_1\cap {\mathcal {K}}$
, we have
![]() $Yw(\pi _{\mathcal {K}}(\alpha ))\gg 1$
and
$Yw(\pi _{\mathcal {K}}(\alpha ))\gg 1$
and
![]() $w(\pi _{\mathcal {K}}(\alpha ))\gg w(\alpha )$
. For any
$w(\pi _{\mathcal {K}}(\alpha ))\gg w(\alpha )$
. For any
![]() $a_{ij}\in ({\mathcal {Z}}_1\cap {\mathcal {K}})\backslash {\mathcal {K}}_{\mathrm {{dist}}}$
, we have
$a_{ij}\in ({\mathcal {Z}}_1\cap {\mathcal {K}})\backslash {\mathcal {K}}_{\mathrm {{dist}}}$
, we have
![]() $i< g+1<j$
. Thus,
$i< g+1<j$
. Thus,
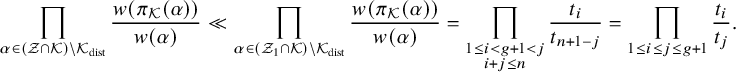 $$ \begin{align*} \prod_{\alpha\in ({\mathcal{Z}}\cap{\mathcal{K}})\backslash {\mathcal{K}}_{\mathrm{{dist}}}} \frac{w(\pi_{\mathcal{K}}(\alpha))}{w(\alpha)} \ll \prod_{\alpha\in ({\mathcal{Z}}_1\cap{\mathcal{K}})\backslash {\mathcal{K}}_{\mathrm{{dist}}}} \frac{w(\pi_{\mathcal{K}}(\alpha))}{w(\alpha)}=\prod_{\substack{1\leq i < g+1 < j \\ i + j \leq n}}\frac{t_i}{t_{n+1-j}}=\prod_{1\leq i\leq j\leq g+1}\frac{t_i}{t_j}. \end{align*} $$
$$ \begin{align*} \prod_{\alpha\in ({\mathcal{Z}}\cap{\mathcal{K}})\backslash {\mathcal{K}}_{\mathrm{{dist}}}} \frac{w(\pi_{\mathcal{K}}(\alpha))}{w(\alpha)} \ll \prod_{\alpha\in ({\mathcal{Z}}_1\cap{\mathcal{K}})\backslash {\mathcal{K}}_{\mathrm{{dist}}}} \frac{w(\pi_{\mathcal{K}}(\alpha))}{w(\alpha)}=\prod_{\substack{1\leq i < g+1 < j \\ i + j \leq n}}\frac{t_i}{t_{n+1-j}}=\prod_{1\leq i\leq j\leq g+1}\frac{t_i}{t_j}. \end{align*} $$
Therefore,
 $$ \begin{align} \nonumber\#\big(s(Y{\mathcal{D}})\cap S({\mathbb{Z}})\big) &\ll Y^{(n+1)(n+2)/2-\#({\mathcal{Z}}\cap{\mathcal{K}})}\prod_{\alpha\in {\mathcal{Z}}\cap{\mathcal{K}}}\frac{1}{w(\alpha)}\\ \nonumber&\ll Y^{(n+1)(n+2)/2-\#({\mathcal{Z}}\cap{\mathcal{K}})}\Big(\prod_{\alpha\in {\mathcal{K}}_{\mathrm{{dist}}}}\frac{1}{w(\alpha)}\Big)\Big(\prod_{\alpha\in ({\mathcal{Z}}\cap{\mathcal{K}})\backslash {\mathcal{K}}_{\mathrm{{dist}}}} \frac{Yw(\pi_q(\alpha))}{w(\alpha)}\Big)\\ \nonumber&\ll \frac{Y^{(n+1)(n+2)/2}}{Y^{\#{\mathcal{K}}_{\mathrm{{dist}}}}}\Big(\prod_{1\leq i\leq j \leq g+1} t_it_j\Big)\Big(\prod_{1\leq i\leq j\leq g+1}\frac{t_i}{t_j}\Big)\\ &= \frac{Y^{(n+1)(n+2)/2}}{Y^{(g+1)(g+2)/2}}(t_1\cdots t_{g+1})^{g+2} \Big(\prod_{1\leq i\leq j\leq g+1}\frac{t_i}{t_j}\Big). \end{align} $$
$$ \begin{align} \nonumber\#\big(s(Y{\mathcal{D}})\cap S({\mathbb{Z}})\big) &\ll Y^{(n+1)(n+2)/2-\#({\mathcal{Z}}\cap{\mathcal{K}})}\prod_{\alpha\in {\mathcal{Z}}\cap{\mathcal{K}}}\frac{1}{w(\alpha)}\\ \nonumber&\ll Y^{(n+1)(n+2)/2-\#({\mathcal{Z}}\cap{\mathcal{K}})}\Big(\prod_{\alpha\in {\mathcal{K}}_{\mathrm{{dist}}}}\frac{1}{w(\alpha)}\Big)\Big(\prod_{\alpha\in ({\mathcal{Z}}\cap{\mathcal{K}})\backslash {\mathcal{K}}_{\mathrm{{dist}}}} \frac{Yw(\pi_q(\alpha))}{w(\alpha)}\Big)\\ \nonumber&\ll \frac{Y^{(n+1)(n+2)/2}}{Y^{\#{\mathcal{K}}_{\mathrm{{dist}}}}}\Big(\prod_{1\leq i\leq j \leq g+1} t_it_j\Big)\Big(\prod_{1\leq i\leq j\leq g+1}\frac{t_i}{t_j}\Big)\\ &= \frac{Y^{(n+1)(n+2)/2}}{Y^{(g+1)(g+2)/2}}(t_1\cdots t_{g+1})^{g+2} \Big(\prod_{1\leq i\leq j\leq g+1}\frac{t_i}{t_j}\Big). \end{align} $$
We now obtain an upper bound on
![]() $\#(s(Y{\mathcal {D}})\cap {\mathcal {S}}(L,s))$
. Recall that
$\#(s(Y{\mathcal {D}})\cap {\mathcal {S}}(L,s))$
. Recall that
Let
![]() $\Lambda \in \Sigma (L,s)$
be a lattice such that
$\Lambda \in \Sigma (L,s)$
be a lattice such that
![]() $s^{-1}(\Lambda )$
has reduced basis
$s^{-1}(\Lambda )$
has reduced basis
![]() $\{\ell _1,\ldots ,\ell _n\}$
with
$\{\ell _1,\ldots ,\ell _n\}$
with
![]() $L_i\leq |\ell _i| < 2L_i$
for each
$L_i\leq |\ell _i| < 2L_i$
for each
![]() $i=1,\ldots ,n$
. Suppose there exists
$i=1,\ldots ,n$
. Suppose there exists
![]() $(A,B)\in (s(Y{\mathcal {D}})\times s(Y{\mathcal {D}}))\cap {{\mathcal {L}}(M)} $
with
$(A,B)\in (s(Y{\mathcal {D}})\times s(Y{\mathcal {D}}))\cap {{\mathcal {L}}(M)} $
with
![]() $B\in s(Y{\mathcal {D}})\cap S(\Lambda )$
. By Proposition 6.26,
$B\in s(Y{\mathcal {D}})\cap S(\Lambda )$
. By Proposition 6.26,
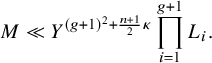 $$ \begin{align} M\ll Y^{(g+1)^2+\frac{n+1}{2}\kappa}\prod_{i=1}^{g+1} L_i. \end{align} $$
$$ \begin{align} M\ll Y^{(g+1)^2+\frac{n+1}{2}\kappa}\prod_{i=1}^{g+1} L_i. \end{align} $$
Recall also from the proof of Proposition 6.26 that
Hence,
It follows that the set
![]() $\{p_1(s\ell _{g+2}),\ldots ,p_1(s\ell _n)\}$
, and thus the set
$\{p_1(s\ell _{g+2}),\ldots ,p_1(s\ell _n)\}$
, and thus the set
![]() $\{p_1(\ell _{g+2}),\ldots ,p_1(\ell _n)\}$
, are both linearly independent. There then exist vectors
$\{p_1(\ell _{g+2}),\ldots ,p_1(\ell _n)\}$
, are both linearly independent. There then exist vectors
![]() $v_{g+2},\ldots ,v_n\in \text {Span}_{\mathbb {R}}\{e_1,\ldots ,e_{g+1}\}$
such that
$v_{g+2},\ldots ,v_n\in \text {Span}_{\mathbb {R}}\{e_1,\ldots ,e_{g+1}\}$
such that
is the identity matrix. Let
![]() $B'\in s(Y{\mathcal {D}})\cap S(\Lambda )$
be any element and write
$B'\in s(Y{\mathcal {D}})\cap S(\Lambda )$
be any element and write
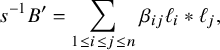 $$ \begin{align*}s^{-1}B' = \sum_{1\leq i\leq j\leq n} \beta_{ij}\ell_i\ast\ell_j,\end{align*} $$
$$ \begin{align*}s^{-1}B' = \sum_{1\leq i\leq j\leq n} \beta_{ij}\ell_i\ast\ell_j,\end{align*} $$
where
![]() $\ell _i\ast \ell _j$
is as defined in (23). Then for
$\ell _i\ast \ell _j$
is as defined in (23). Then for
![]() $g+2\leq i\leq j\leq n$
, since
$g+2\leq i\leq j\leq n$
, since
![]() $v_i,v_j\perp \ell _1,\ldots ,\ell _{g+2}$
, we have
$v_i,v_j\perp \ell _1,\ldots ,\ell _{g+2}$
, we have
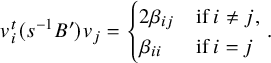 $$ \begin{align*}v_i^t (s^{-1}B') v_j = \begin{cases} 2\beta_{ij} &\text{if }i\neq j,\\ \beta_{ii}&\text{if }i=j\end{cases}.\end{align*} $$
$$ \begin{align*}v_i^t (s^{-1}B') v_j = \begin{cases} 2\beta_{ij} &\text{if }i\neq j,\\ \beta_{ii}&\text{if }i=j\end{cases}.\end{align*} $$
Since the top left
![]() $(g+1)\times (g+1)$
block of
$(g+1)\times (g+1)$
block of
![]() $B'\in s(Y{\mathcal {D}})\cap S(\Lambda )$
is
$B'\in s(Y{\mathcal {D}})\cap S(\Lambda )$
is
![]() $0$
, the same is true for
$0$
, the same is true for
![]() $s^{-1}B'$
. Hence,
$s^{-1}B'$
. Hence,
![]() $\beta _{ij} = 0$
whenever
$\beta _{ij} = 0$
whenever
![]() $g+2\leq i\leq j\leq n$
. In other words,
$g+2\leq i\leq j\leq n$
. In other words,
By Proposition 5.2, we have
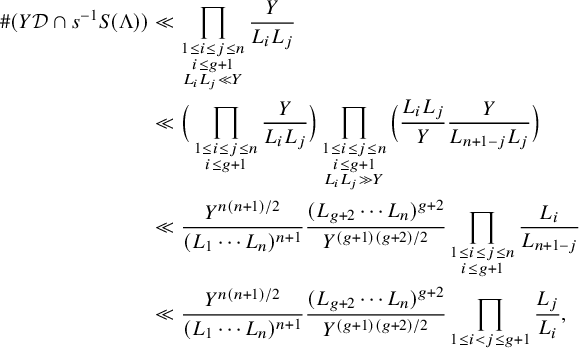 $$ \begin{align} \nonumber\#(Y{\mathcal{D}} \cap s^{-1}S(\Lambda))&\ll \prod_{\substack{1\leq i \leq j\leq n\\i\leq g+1\\L_iL_j\ll Y}}\frac{Y}{L_iL_j}\\ \nonumber&\ll \Big(\prod_{\substack{1\leq i \leq j\leq n\\i\leq g+1}}\frac{Y}{L_iL_j}\Big)\prod_{\substack{1\leq i\leq j\leq n\\i\leq g+1\\L_iL_j\gg Y}}\Big(\frac{L_iL_j}{Y}\frac{Y}{L_{n+1-j}{L_j}}\Big)\\ \nonumber&\ll \frac{Y^{n(n+1)/2}}{(L_1\cdots L_n)^{n+1}}\frac{(L_{g+2}\cdots L_n)^{g+2}}{Y^{(g+1)(g+2)/2}}\prod_{\substack{1\leq i\leq j\leq n\\i\leq g+1}}\frac{L_i}{L_{n+1-j}}\\ &\ll\frac{Y^{n(n+1)/2}}{(L_1\cdots L_n)^{n+1}}\frac{(L_{g+2}\cdots L_n)^{g+2}}{Y^{(g+1)(g+2)/2}}\prod_{1\leq i< j\leq g+1}\frac{L_j}{L_i}, \end{align} $$
$$ \begin{align} \nonumber\#(Y{\mathcal{D}} \cap s^{-1}S(\Lambda))&\ll \prod_{\substack{1\leq i \leq j\leq n\\i\leq g+1\\L_iL_j\ll Y}}\frac{Y}{L_iL_j}\\ \nonumber&\ll \Big(\prod_{\substack{1\leq i \leq j\leq n\\i\leq g+1}}\frac{Y}{L_iL_j}\Big)\prod_{\substack{1\leq i\leq j\leq n\\i\leq g+1\\L_iL_j\gg Y}}\Big(\frac{L_iL_j}{Y}\frac{Y}{L_{n+1-j}{L_j}}\Big)\\ \nonumber&\ll \frac{Y^{n(n+1)/2}}{(L_1\cdots L_n)^{n+1}}\frac{(L_{g+2}\cdots L_n)^{g+2}}{Y^{(g+1)(g+2)/2}}\prod_{\substack{1\leq i\leq j\leq n\\i\leq g+1}}\frac{L_i}{L_{n+1-j}}\\ &\ll\frac{Y^{n(n+1)/2}}{(L_1\cdots L_n)^{n+1}}\frac{(L_{g+2}\cdots L_n)^{g+2}}{Y^{(g+1)(g+2)/2}}\prod_{1\leq i< j\leq g+1}\frac{L_j}{L_i}, \end{align} $$
where the second bound follows since
![]() $L_{n+1-j}L_j\ll Y$
for all j by Proposition 5.4; and the last bound follows because the map from
$L_{n+1-j}L_j\ll Y$
for all j by Proposition 5.4; and the last bound follows because the map from
![]() $\{(i,j):1\leq i\leq j\leq n\text { and }i\leq g+1\}$
to
$\{(i,j):1\leq i\leq j\leq n\text { and }i\leq g+1\}$
to
![]() $\{(k,\ell )\}$
sending
$\{(k,\ell )\}$
sending
![]() $(i,j)$
to
$(i,j)$
to
![]() $(n+1-j,i)$
is one-to-one with its image contained within the set of pairs
$(n+1-j,i)$
is one-to-one with its image contained within the set of pairs
![]() $(k,\ell )$
with
$(k,\ell )$
with
![]() $k<\ell \leq g+1$
, and because the
$k<\ell \leq g+1$
, and because the
![]() $L_i$
’s are nondecreasing.
$L_i$
’s are nondecreasing.
To obtain a bound on the size of
![]() $\Sigma (L,s)$
, we use (43):
$\Sigma (L,s)$
, we use (43):
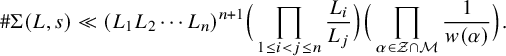 $$ \begin{align*} \#\Sigma(L,s)\ll (L_1L_2\cdots L_n)^{n+1} \Big(\prod_{1\leq i<j\leq n}\frac{L_i}{L_j}\Big) \Big(\prod_{\alpha\in{\mathcal{Z}}\cap{\mathcal{M}}} \frac{1}{w(\alpha)}\Big). \end{align*} $$
$$ \begin{align*} \#\Sigma(L,s)\ll (L_1L_2\cdots L_n)^{n+1} \Big(\prod_{1\leq i<j\leq n}\frac{L_i}{L_j}\Big) \Big(\prod_{\alpha\in{\mathcal{Z}}\cap{\mathcal{M}}} \frac{1}{w(\alpha)}\Big). \end{align*} $$
Let
![]() ${\mathcal {M}}_{\mathrm {{dist}}} = \{\ell _{i,j}\mid 1\leq i\leq g+1,\,1\leq j\leq g+1\}$
. Recall that elements
${\mathcal {M}}_{\mathrm {{dist}}} = \{\ell _{i,j}\mid 1\leq i\leq g+1,\,1\leq j\leq g+1\}$
. Recall that elements
![]() $\ell _{i,j}\in {\mathcal {Z}}_1$
satisfy
$\ell _{i,j}\in {\mathcal {Z}}_1$
satisfy
![]() $i+j\leq n+1$
. Hence, for any
$i+j\leq n+1$
. Hence, for any
![]() $\ell _{ij}\in ({\mathcal {Z}}_1\cap {\mathcal {M}})\backslash {\mathcal {M}}_{\mathrm {{dist}}}$
, exactly one of i and j is
$\ell _{ij}\in ({\mathcal {Z}}_1\cap {\mathcal {M}})\backslash {\mathcal {M}}_{\mathrm {{dist}}}$
, exactly one of i and j is
![]() $\leq g+1$
. Define
$\leq g+1$
. Define
 $$ \begin{align*} \begin{array}{rcl} \pi_{\mathcal{M}}&:&({\mathcal{Z}}_1\cap{\mathcal{M}})\backslash {\mathcal{M}}_{\mathrm{{dist}}}\to{\mathcal{M}}\\[.1in] \pi_{\mathcal{M}}(\ell_{i,j}) &=& \left\{ \begin{array}{rl} \ell_{i,n+2-i}&\;\mathrm{if}\; i\leq g+1;\\ \ell_{n+1-j,j} &\;\mathrm{if}\; j \leq g+1. \end{array}\right. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{rcl} \pi_{\mathcal{M}}&:&({\mathcal{Z}}_1\cap{\mathcal{M}})\backslash {\mathcal{M}}_{\mathrm{{dist}}}\to{\mathcal{M}}\\[.1in] \pi_{\mathcal{M}}(\ell_{i,j}) &=& \left\{ \begin{array}{rl} \ell_{i,n+2-i}&\;\mathrm{if}\; i\leq g+1;\\ \ell_{n+1-j,j} &\;\mathrm{if}\; j \leq g+1. \end{array}\right. \end{array} \end{align*} $$
We claim that the image of
![]() $\pi _{\mathcal {M}}$
is disjoint from
$\pi _{\mathcal {M}}$
is disjoint from
![]() ${\mathcal {Z}}$
. Indeed, when
${\mathcal {Z}}$
. Indeed, when
![]() $i\leq g+1$
, we have
$i\leq g+1$
, we have
![]() $\pi _{\mathcal {M}}(\ell _{i,j})\not \in {\mathcal {Z}}_1$
, and when
$\pi _{\mathcal {M}}(\ell _{i,j})\not \in {\mathcal {Z}}_1$
, and when
![]() $j\leq g+1$
, we have
$j\leq g+1$
, we have
![]() $\pi _{\mathcal {M}}(\ell _{i,j})\not \in {\mathcal {Z}}$
by Lemma 6.5 and the fact that
$\pi _{\mathcal {M}}(\ell _{i,j})\not \in {\mathcal {Z}}$
by Lemma 6.5 and the fact that
![]() $a_{g+1,g+1}\in {\mathcal {Z}}$
. Thus,
$a_{g+1,g+1}\in {\mathcal {Z}}$
. Thus,
![]() $w(\pi _{\mathcal {M}}(\alpha ))\gg 1$
and
$w(\pi _{\mathcal {M}}(\alpha ))\gg 1$
and
![]() $w(\pi _{\mathcal {M}}(\alpha ))\gg w(\alpha )$
for every
$w(\pi _{\mathcal {M}}(\alpha ))\gg w(\alpha )$
for every
![]() $\alpha \in ({\mathcal {Z}}_1\cap {\mathcal {M}})\backslash {\mathcal {M}}_{\mathrm {{dist}}}$
. It follows that
$\alpha \in ({\mathcal {Z}}_1\cap {\mathcal {M}})\backslash {\mathcal {M}}_{\mathrm {{dist}}}$
. It follows that
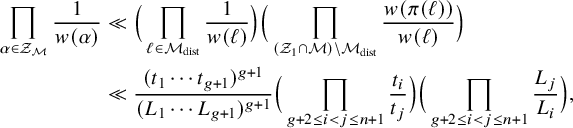 $$ \begin{align*} \prod_{\alpha\in{\mathcal{Z}}_{\mathcal{M}}}\frac{1}{w(\alpha)} &\ll \Big(\prod_{\ell\in {\mathcal{M}}_{\mathrm{{dist}}}}\frac{1}{w(\ell)} \Big)\Big(\prod_{({\mathcal{Z}}_1\cap{\mathcal{M}})\backslash{\mathcal{M}}_{\mathrm{{dist}}}}\frac{w(\pi(\ell))}{w(\ell)}\Big) \\ &\ll \frac{(t_1\cdots t_{g+1})^{g+1}}{(L_1\cdots L_{g+1})^{g+1}} \Big(\prod_{g+2\leq i< j\leq n+1}\frac{t_i}{t_j}\Big) \Big(\prod_{g+2\leq i< j\leq n+1}\frac{L_j}{L_i}\Big), \end{align*} $$
$$ \begin{align*} \prod_{\alpha\in{\mathcal{Z}}_{\mathcal{M}}}\frac{1}{w(\alpha)} &\ll \Big(\prod_{\ell\in {\mathcal{M}}_{\mathrm{{dist}}}}\frac{1}{w(\ell)} \Big)\Big(\prod_{({\mathcal{Z}}_1\cap{\mathcal{M}})\backslash{\mathcal{M}}_{\mathrm{{dist}}}}\frac{w(\pi(\ell))}{w(\ell)}\Big) \\ &\ll \frac{(t_1\cdots t_{g+1})^{g+1}}{(L_1\cdots L_{g+1})^{g+1}} \Big(\prod_{g+2\leq i< j\leq n+1}\frac{t_i}{t_j}\Big) \Big(\prod_{g+2\leq i< j\leq n+1}\frac{L_j}{L_i}\Big), \end{align*} $$
so that
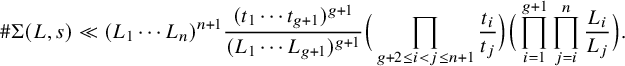 $$ \begin{align} \#\Sigma(L,s) \ll (L_1\cdots L_n)^{n+1}\frac{(t_1\cdots t_{g+1})^{g+1}}{(L_1\cdots L_{g+1})^{g+1}}\Big(\prod_{g+2\leq i< j\leq n+1}\frac{t_i}{t_j}\Big)\Big(\prod_{i=1}^{g+1}\prod_{j=i}^n \frac{L_i}{L_j}\Big). \end{align} $$
$$ \begin{align} \#\Sigma(L,s) \ll (L_1\cdots L_n)^{n+1}\frac{(t_1\cdots t_{g+1})^{g+1}}{(L_1\cdots L_{g+1})^{g+1}}\Big(\prod_{g+2\leq i< j\leq n+1}\frac{t_i}{t_j}\Big)\Big(\prod_{i=1}^{g+1}\prod_{j=i}^n \frac{L_i}{L_j}\Big). \end{align} $$
Combining (74), (76) and (77) and the identity
 $$ \begin{align*} \Big(\prod_{1\leq i< j\leq g+1}\frac{L_j}{L_i}\Big)\Big(\prod_{i=1}^{g+1}\prod_{j=i}^n \frac{L_i}{L_j}\Big) = \frac{(L_1\cdots L_{g+1})^{g+1}}{(L_{g+2}\cdots L_n)^{g+1}} \end{align*} $$
$$ \begin{align*} \Big(\prod_{1\leq i< j\leq g+1}\frac{L_j}{L_i}\Big)\Big(\prod_{i=1}^{g+1}\prod_{j=i}^n \frac{L_i}{L_j}\Big) = \frac{(L_1\cdots L_{g+1})^{g+1}}{(L_{g+2}\cdots L_n)^{g+1}} \end{align*} $$
now yields
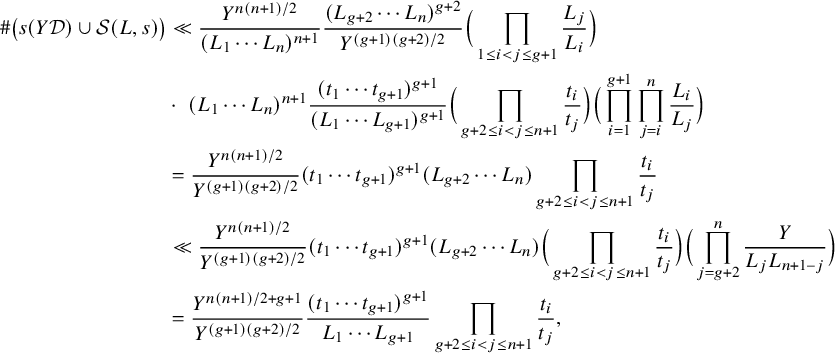 $$ \begin{align} \nonumber\#\big(s(Y{\mathcal{D}})\cup{\mathcal{S}}(L,s)\big) &\ll \frac{Y^{n(n+1)/2}}{(L_1\cdots L_n)^{n+1}} \frac{(L_{g+2}\cdots L_n)^{g+2}}{Y^{(g+1)(g+2)/2}} \Big(\prod_{1\leq i< j\leq g+1}\frac{L_j}{L_i}\Big)\\ \nonumber&\cdot \,\,(L_1\cdots L_n)^{n+1} \frac{(t_1\cdots t_{g+1})^{g+1}}{(L_1\cdots L_{g+1})^{g+1}} \Big(\prod_{g+2\leq i< j\leq n+1}\frac{t_i}{t_j}\Big) \Big(\prod_{i=1}^{g+1}\prod_{j=i}^n \frac{L_i}{L_j}\Big)\\ \nonumber&= \frac{Y^{n(n+1)/2}}{Y^{(g+1)(g+2)/2}}(t_1\cdots t_{g+1})^{g+1}(L_{g+2}\cdots L_n) \prod_{g+2\leq i< j\leq n+1}\frac{t_i}{t_j}\\ \nonumber&\ll \frac{Y^{n(n+1)/2}}{Y^{(g+1)(g+2)/2}}(t_1\cdots t_{g+1})^{g+1}(L_{g+2}\cdots L_n) \Big(\prod_{g+2\leq i< j\leq n+1}\frac{t_i}{t_j}\Big) \Big(\prod_{j=g+2}^n\frac{Y}{L_jL_{n+1-j}}\Big)\\ &= \frac{Y^{n(n+1)/2+g+1}}{Y^{(g+1)(g+2)/2}}\frac{(t_1\cdots t_{g+1})^{g+1}}{L_1\cdots L_{g+1}}\prod_{g+2\leq i< j\leq n+1}\frac{t_i}{t_j}, \end{align} $$
$$ \begin{align} \nonumber\#\big(s(Y{\mathcal{D}})\cup{\mathcal{S}}(L,s)\big) &\ll \frac{Y^{n(n+1)/2}}{(L_1\cdots L_n)^{n+1}} \frac{(L_{g+2}\cdots L_n)^{g+2}}{Y^{(g+1)(g+2)/2}} \Big(\prod_{1\leq i< j\leq g+1}\frac{L_j}{L_i}\Big)\\ \nonumber&\cdot \,\,(L_1\cdots L_n)^{n+1} \frac{(t_1\cdots t_{g+1})^{g+1}}{(L_1\cdots L_{g+1})^{g+1}} \Big(\prod_{g+2\leq i< j\leq n+1}\frac{t_i}{t_j}\Big) \Big(\prod_{i=1}^{g+1}\prod_{j=i}^n \frac{L_i}{L_j}\Big)\\ \nonumber&= \frac{Y^{n(n+1)/2}}{Y^{(g+1)(g+2)/2}}(t_1\cdots t_{g+1})^{g+1}(L_{g+2}\cdots L_n) \prod_{g+2\leq i< j\leq n+1}\frac{t_i}{t_j}\\ \nonumber&\ll \frac{Y^{n(n+1)/2}}{Y^{(g+1)(g+2)/2}}(t_1\cdots t_{g+1})^{g+1}(L_{g+2}\cdots L_n) \Big(\prod_{g+2\leq i< j\leq n+1}\frac{t_i}{t_j}\Big) \Big(\prod_{j=g+2}^n\frac{Y}{L_jL_{n+1-j}}\Big)\\ &= \frac{Y^{n(n+1)/2+g+1}}{Y^{(g+1)(g+2)/2}}\frac{(t_1\cdots t_{g+1})^{g+1}}{L_1\cdots L_{g+1}}\prod_{g+2\leq i< j\leq n+1}\frac{t_i}{t_j}, \end{align} $$
where the fourth line follows since
![]() $L_{n+1-j}L_j\ll Y$
for all j by Proposition 5.4. Finally, note that
$L_{n+1-j}L_j\ll Y$
for all j by Proposition 5.4. Finally, note that
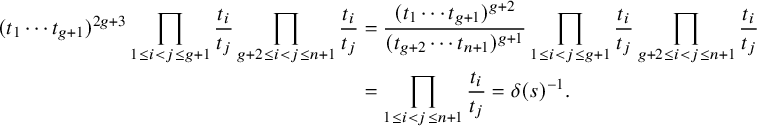 $$ \begin{align*} (t_1\cdots t_{g+1})^{2g+3} \prod_{1\leq i< j\leq g+1}\frac{t_i}{t_j} \prod_{g+2\leq i< j\leq n+1}\frac{t_i}{t_j} &=\frac{(t_1\cdots t_{g+1})^{g+2}}{(t_{g+2}\cdots t_{n+1})^{g+1}} \prod_{1\leq i< j\leq g+1}\frac{t_i}{t_j} \prod_{g+2\leq i< j\leq n+1}\frac{t_i}{t_j} \\ &= \prod_{1\leq i< j\leq n+1}\frac{t_i}{t_j} = \delta(s)^{-1}. \end{align*} $$
$$ \begin{align*} (t_1\cdots t_{g+1})^{2g+3} \prod_{1\leq i< j\leq g+1}\frac{t_i}{t_j} \prod_{g+2\leq i< j\leq n+1}\frac{t_i}{t_j} &=\frac{(t_1\cdots t_{g+1})^{g+2}}{(t_{g+2}\cdots t_{n+1})^{g+1}} \prod_{1\leq i< j\leq g+1}\frac{t_i}{t_j} \prod_{g+2\leq i< j\leq n+1}\frac{t_i}{t_j} \\ &= \prod_{1\leq i< j\leq n+1}\frac{t_i}{t_j} = \delta(s)^{-1}. \end{align*} $$
Therefore, combining (73), (75) and (78) gives
 $$ \begin{align*} N({{\mathcal{L}}(M)} ,L,{\mathcal{Z}},X)&\ll \int_{T_{\mathcal{Z}}(L,Y)}\#\big(s(Y{\mathcal{D}})\cap S({\mathbb{Z}})\big)\cdot\#\big( s(Y{\mathcal{D}})\cap{\mathcal{S}}(L,s)\big)\, \delta(s)d^\times s \\ &\ll \frac{Y^{(n+1)^2-(g+1)^2}}{L_1\cdots L_{g+1}}\int_{T_{\mathcal{Z}}(L,Y)}d^\times s \\ &\ll \frac{X^{(n+1)+\frac12\kappa}}{M}\log^n Y. \end{align*} $$
$$ \begin{align*} N({{\mathcal{L}}(M)} ,L,{\mathcal{Z}},X)&\ll \int_{T_{\mathcal{Z}}(L,Y)}\#\big(s(Y{\mathcal{D}})\cap S({\mathbb{Z}})\big)\cdot\#\big( s(Y{\mathcal{D}})\cap{\mathcal{S}}(L,s)\big)\, \delta(s)d^\times s \\ &\ll \frac{Y^{(n+1)^2-(g+1)^2}}{L_1\cdots L_{g+1}}\int_{T_{\mathcal{Z}}(L,Y)}d^\times s \\ &\ll \frac{X^{(n+1)+\frac12\kappa}}{M}\log^n Y. \end{align*} $$
Theorem 6.24 now follows immediately from (72) by summing over the
![]() $O(1)$
different possible
$O(1)$
different possible
![]() ${\mathcal {Z}}$
’s and the
${\mathcal {Z}}$
’s and the
![]() $O(\log ^n Y)$
different possible L’s.
$O(\log ^n Y)$
different possible L’s.
6.5 Proof of the main uniformity estimates
Proof of Theorem 5.
Case (a) of Theorem 5 follows from an application of the quantitative version of the Ekedahl geometric sieve developed in [Reference Bhargava4, Theorem 3.3]. Case (b) follows from (14), (16), and Theorem 4.2.
We now use the results of this section to prove the most intricate case – namely, Case (c). For any prime p, the number binary n-ic forms mod
![]() $p^2$
having discriminant
$p^2$
having discriminant
![]() $0$
mod
$0$
mod
![]() $p^2$
is
$p^2$
is
![]() $O(p^{2n})$
since the p-adic densities of these forms is
$O(p^{2n})$
since the p-adic densities of these forms is
![]() $O(1/p^2)$
by Proposition A.1. For any squarefree m, we then have
$O(1/p^2)$
by Proposition A.1. For any squarefree m, we then have
![]() $O_\epsilon (m^{2n-\epsilon })$
binary n-ic forms mod
$O_\epsilon (m^{2n-\epsilon })$
binary n-ic forms mod
![]() $m^2$
having discriminant
$m^2$
having discriminant
![]() $0$
mod
$0$
mod
![]() $m^2$
. Hence, for any squarefree
$m^2$
. Hence, for any squarefree
![]() $m \leq X^{1/2}$
, we have the bound
$m \leq X^{1/2}$
, we have the bound
Using this bound for
![]() $m\leq X^{1/2}$
, we may assume that
$m\leq X^{1/2}$
, we may assume that
![]() $M>X^{1/2}$
. We note next that from (35), (37), and Lemmas 6.1 and 6.2, we have
$M>X^{1/2}$
. We note next that from (35), (37), and Lemmas 6.1 and 6.2, we have
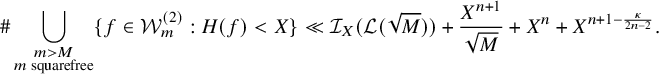 $$ \begin{align*} \#\bigcup_{\substack{m>M\\ m\;\mathrm{ squarefree} }}\{f\in{\mathcal{W}}_m^{\mathrm{{{(2)}}}}:H(f)<X\} \ll {\mathcal{I}}_X({\mathcal{L}}(\sqrt{M}))+\frac{X^{n+1}}{\sqrt{M}}+X^{n}+X^{n+1-\frac{\kappa}{2n-2}}. \end{align*} $$
$$ \begin{align*} \#\bigcup_{\substack{m>M\\ m\;\mathrm{ squarefree} }}\{f\in{\mathcal{W}}_m^{\mathrm{{{(2)}}}}:H(f)<X\} \ll {\mathcal{I}}_X({\mathcal{L}}(\sqrt{M}))+\frac{X^{n+1}}{\sqrt{M}}+X^{n}+X^{n+1-\frac{\kappa}{2n-2}}. \end{align*} $$
Applying Theorems 6.6, 6.11 and 6.24, we obtain
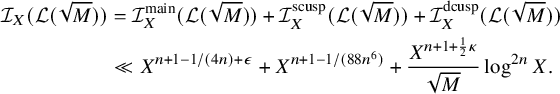 $$ \begin{align*} {\mathcal{I}}_X({\mathcal{L}}(\sqrt{M}))&={\mathcal{I}}_X^{\mathrm{{main}}}({\mathcal{L}}(\sqrt{M}))+{\mathcal{I}}_X^{\mathrm{{scusp}}}({\mathcal{L}}(\sqrt{M}))+{\mathcal{I}}_X^{\mathrm{{dcusp}}}({\mathcal{L}}(\sqrt{M})) \\ &\ll X^{n+1-1/(4n)+\epsilon}+X^{n+1-1/(88n^6)}+\frac{X^{n+1+\frac12\kappa}}{\sqrt{M}}\log^{2n}X. \end{align*} $$
$$ \begin{align*} {\mathcal{I}}_X({\mathcal{L}}(\sqrt{M}))&={\mathcal{I}}_X^{\mathrm{{main}}}({\mathcal{L}}(\sqrt{M}))+{\mathcal{I}}_X^{\mathrm{{scusp}}}({\mathcal{L}}(\sqrt{M}))+{\mathcal{I}}_X^{\mathrm{{dcusp}}}({\mathcal{L}}(\sqrt{M})) \\ &\ll X^{n+1-1/(4n)+\epsilon}+X^{n+1-1/(88n^6)}+\frac{X^{n+1+\frac12\kappa}}{\sqrt{M}}\log^{2n}X. \end{align*} $$
Setting
![]() $\kappa = (2n-2)/(88n^6)$
yields the desired result.
$\kappa = (2n-2)/(88n^6)$
yields the desired result.
Theorem 5 has the following immediate consequence. For a positive squarefree integer m, let
![]() ${\mathcal {W}}_m$
denote the set of integral binary n-ic forms whose discriminants are divisible by
${\mathcal {W}}_m$
denote the set of integral binary n-ic forms whose discriminants are divisible by
![]() $m^2$
.
$m^2$
.
Corollary 6.27. For a positive integer
![]() $N\geq 3$
, and positive real numbers M and X, we have
$N\geq 3$
, and positive real numbers M and X, we have
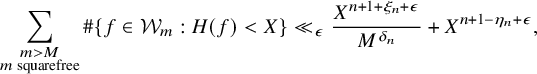 $$ \begin{align*} \sum_{\substack{m>M\\m \textrm{ squarefree}}}\#\{f\in {\mathcal{W}}_{m}:H(f)<X\} \ll_\epsilon \frac{X^{n+1+\xi_n+\epsilon}}{M^{\delta_n}}+X^{n+1-{\eta_n}+\epsilon}, \end{align*} $$
$$ \begin{align*} \sum_{\substack{m>M\\m \textrm{ squarefree}}}\#\{f\in {\mathcal{W}}_{m}:H(f)<X\} \ll_\epsilon \frac{X^{n+1+\xi_n+\epsilon}}{M^{\delta_n}}+X^{n+1-{\eta_n}+\epsilon}, \end{align*} $$
where
![]() $\delta _n=1/2,\,\xi _n = 0,\,\eta _n=1/(2n)$
when n is odd and
$\delta _n=1/2,\,\xi _n = 0,\,\eta _n=1/(2n)$
when n is odd and
![]() $\delta _n=1/3,\,\xi _n = 1/(88n^5),\,\eta _n=1/(88n^6)$
when n is even.
$\delta _n=1/3,\,\xi _n = 1/(88n^5),\,\eta _n=1/(88n^6)$
when n is even.
Proof. Suppose
![]() $f\in {\mathcal {W}}_{m}$
for some squarefree
$f\in {\mathcal {W}}_{m}$
for some squarefree
![]() $m>M$
. Note that for a fixed f, the number of such
$m>M$
. Note that for a fixed f, the number of such
![]() $m> M$
such that
$m> M$
such that
![]() $f\in {\mathcal {W}}_m$
is
$f\in {\mathcal {W}}_m$
is
![]() $\ll _\epsilon X^\epsilon $
. Hence, it suffices to consider the cardinality of the union over squarefree
$\ll _\epsilon X^\epsilon $
. Hence, it suffices to consider the cardinality of the union over squarefree
![]() $m>M$
. Let
$m>M$
. Let
![]() $m_1$
be the product of primes
$m_1$
be the product of primes
![]() $p\mid m$
such that
$p\mid m$
such that
![]() $f\in {\mathcal {W}}_p^{(1)}$
. Let
$f\in {\mathcal {W}}_p^{(1)}$
. Let
![]() $m_2$
be the product of primes
$m_2$
be the product of primes
![]() $p\mid m$
such that
$p\mid m$
such that
![]() $f\in {\mathcal {W}}_p^{(2)}$
. Then
$f\in {\mathcal {W}}_p^{(2)}$
. Then
![]() $m_1m_2 = m$
. For any positive real numbers
$m_1m_2 = m$
. For any positive real numbers
![]() $M_1,M_2$
such that
$M_1,M_2$
such that
![]() $M_1M_2 = M$
, we have either
$M_1M_2 = M$
, we have either
![]() $m_1> M_1$
or
$m_1> M_1$
or
![]() $m_2> M_2$
, and so
$m_2> M_2$
, and so
 $$ \begin{align*} \#\bigcup_{\substack{m>M\\ m \textrm{ squarefree}}}\#\{f\in {\mathcal{W}}_{m}:H(f)<X\} &\leq \#\bigcup_{\substack{m>M_1\\ m \textrm{ squarefree}}}\#\{f\in {\mathcal{W}}_{m}^{(1)}:H(f)<X\},\\ \#\bigcup_{\substack{m>M\\ m \textrm{ squarefree}}}\#\{f\in {\mathcal{W}}_{m}:H(f)<X\} &\leq \#\bigcup_{\substack{m>M_2\\ m \textrm{ squarefree}}}\#\{f\in {\mathcal{W}}_{m}^{(2)}:H(f)<X\}. \end{align*} $$
$$ \begin{align*} \#\bigcup_{\substack{m>M\\ m \textrm{ squarefree}}}\#\{f\in {\mathcal{W}}_{m}:H(f)<X\} &\leq \#\bigcup_{\substack{m>M_1\\ m \textrm{ squarefree}}}\#\{f\in {\mathcal{W}}_{m}^{(1)}:H(f)<X\},\\ \#\bigcup_{\substack{m>M\\ m \textrm{ squarefree}}}\#\{f\in {\mathcal{W}}_{m}:H(f)<X\} &\leq \#\bigcup_{\substack{m>M_2\\ m \textrm{ squarefree}}}\#\{f\in {\mathcal{W}}_{m}^{(2)}:H(f)<X\}. \end{align*} $$
Optimizing, we take
![]() $M_1 = M_2 = \sqrt {M}$
when n is odd, and take
$M_1 = M_2 = \sqrt {M}$
when n is odd, and take
![]() $M_1 = M^{1/3}$
,
$M_1 = M^{1/3}$
,
![]() $M_2 = M^{2/3}$
when n is even. A direct application of Theorem 5 now yields the result.
$M_2 = M^{2/3}$
when n is even. A direct application of Theorem 5 now yields the result.
7 Proofs of the main results
We begin by proving a more general form of Theorem 6. Let N be a positive squarefree integer, and for each
![]() $p\mid N$
, let
$p\mid N$
, let
![]() $\Sigma _p\subset V_n({\mathbb {Z}}/p^2{\mathbb {Z}})$
be a nonempty subset. Denote the collection
$\Sigma _p\subset V_n({\mathbb {Z}}/p^2{\mathbb {Z}})$
be a nonempty subset. Denote the collection
![]() $(\Sigma _p)_{p\mid N}$
by
$(\Sigma _p)_{p\mid N}$
by
![]() $\Sigma $
. Let
$\Sigma $
. Let
![]() $V_n(\Sigma )$
be the set of all
$V_n(\Sigma )$
be the set of all
![]() $f\in V_n({\mathbb {Z}})$
such that the reduction of f modulo
$f\in V_n({\mathbb {Z}})$
such that the reduction of f modulo
![]() $p^2$
lies in
$p^2$
lies in
![]() $\Sigma _p$
for all
$\Sigma _p$
for all
![]() $p\mid N$
. For
$p\mid N$
. For
![]() $p\mid N$
, let
$p\mid N$
, let
![]() $\alpha _n(\Sigma ,p)$
(resp.,
$\alpha _n(\Sigma ,p)$
(resp.,
![]() $\beta _n(\Sigma ,p)$
) denote the density of elements
$\beta _n(\Sigma ,p)$
) denote the density of elements
![]() $f\in V_n({\mathbb {Z}})$
such that
$f\in V_n({\mathbb {Z}})$
such that
![]() $p^2\nmid \Delta (f)$
(resp.,
$p^2\nmid \Delta (f)$
(resp.,
![]() $R_f$
is maximal at p) and such that the reduction of f modulo
$R_f$
is maximal at p) and such that the reduction of f modulo
![]() $p^2$
lies in
$p^2$
lies in
![]() $\Sigma _p$
. For
$\Sigma _p$
. For
![]() $p\nmid N$
, simply set
$p\nmid N$
, simply set
![]() $\alpha _n(\Sigma ,p)=\alpha _n(p)$
and
$\alpha _n(\Sigma ,p)=\alpha _n(p)$
and
![]() $\beta _n(\Sigma ,p)=\beta _n(p)$
. Finally, define
$\beta _n(\Sigma ,p)=\beta _n(p)$
. Finally, define
We are now ready to carry out our sieve.
Theorem 7.1. We have
 $$ \begin{align*} \begin{array}{ccl} \#\{f\in V_n(\Sigma): H(f)<X\text{ and } \Delta(f)\text{ squarefree}\}&\!\!=\!\!& \alpha_n(\Sigma)(2X)^{n+1} + O_\epsilon(\mathcal{E}(X,N,\epsilon)), \\[.115in] \#\{f\in V_n(\Sigma): H(f)<X\text{ and }R_f\text{ maximal}\}&\!\!=\!\!& \beta_n(\Sigma)(2X)^{n+1} + O_\epsilon(\mathcal{E}(X,N,\epsilon)), \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{ccl} \#\{f\in V_n(\Sigma): H(f)<X\text{ and } \Delta(f)\text{ squarefree}\}&\!\!=\!\!& \alpha_n(\Sigma)(2X)^{n+1} + O_\epsilon(\mathcal{E}(X,N,\epsilon)), \\[.115in] \#\{f\in V_n(\Sigma): H(f)<X\text{ and }R_f\text{ maximal}\}&\!\!=\!\!& \beta_n(\Sigma)(2X)^{n+1} + O_\epsilon(\mathcal{E}(X,N,\epsilon)), \end{array} \end{align*} $$
where the error term is given by
where
![]() $\eta _n = 1/(2n),\, \xi _n = 0$
when n is odd, and
$\eta _n = 1/(2n),\, \xi _n = 0$
when n is odd, and
![]() $\eta _n = 1/(88n^6),\,\xi _n = 1/(88n^5)$
when n is even.
$\eta _n = 1/(88n^6),\,\xi _n = 1/(88n^5)$
when n is even.
Proof. For any squarefree integer m that is relatively prime to N, let
![]() ${\mathcal {W}}_{m}(\Sigma )$
denote the set of elements
${\mathcal {W}}_{m}(\Sigma )$
denote the set of elements
![]() $f\in V({\mathbb {Z}})$
such that
$f\in V({\mathbb {Z}})$
such that
![]() $m^2\mid \Delta (f)$
, and such that the reduction of f modulo
$m^2\mid \Delta (f)$
, and such that the reduction of f modulo
![]() $p^2$
belongs to
$p^2$
belongs to
![]() $\Sigma _p$
for every
$\Sigma _p$
for every
![]() $p\mid N$
. Note that
$p\mid N$
. Note that
![]() ${\mathcal {W}}_m(\Sigma )$
is a union of
${\mathcal {W}}_m(\Sigma )$
is a union of
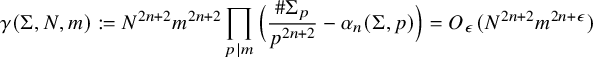 $$ \begin{align*}\gamma(\Sigma,N,m) := N^{2n+2}m^{2n+2}\prod_{p\mid m}\Big(\frac{\#\Sigma_p}{p^{2n+2}} - \alpha_n(\Sigma,p)\Big) = O_\epsilon(N^{2n+2}m^{2n+\epsilon})\end{align*} $$
$$ \begin{align*}\gamma(\Sigma,N,m) := N^{2n+2}m^{2n+2}\prod_{p\mid m}\Big(\frac{\#\Sigma_p}{p^{2n+2}} - \alpha_n(\Sigma,p)\Big) = O_\epsilon(N^{2n+2}m^{2n+\epsilon})\end{align*} $$
translates of
![]() $m^2N^2V({\mathbb {Z}})$
. By inclusion-exclusion and Corollary 6.27, we have for any
$m^2N^2V({\mathbb {Z}})$
. By inclusion-exclusion and Corollary 6.27, we have for any
![]() $M>0$
,
$M>0$
,
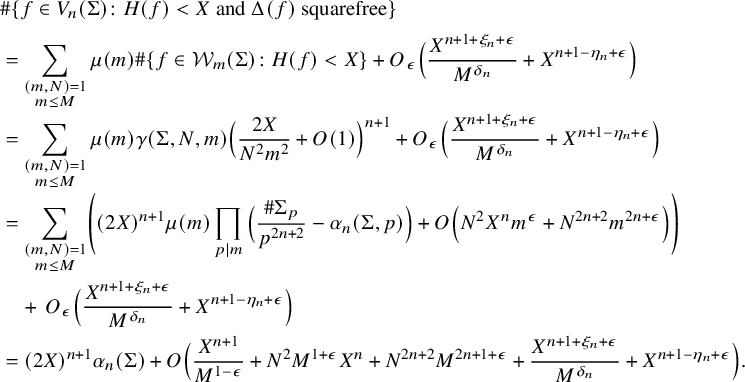 $$ \begin{align*} \nonumber&\#\{f\in V_n(\Sigma)\colon H(f)<X\text{ and } \Delta(f)\text{ squarefree}\}\\[.025in]\nonumber &=\sum_{\substack{(m,N)=1\\m\leq M}} \mu(m)\#\{f\in {\mathcal{W}}_m(\Sigma)\colon H(f)<X\} + O_\epsilon\Big(\frac{X^{n+1+\xi_n+\epsilon}}{M^{\delta_n}}+X^{n+1-{\eta_n}+\epsilon}\Big)\\[-.025in]\nonumber&=\sum_{\substack{(m,N)=1\\m\leq M}} \mu(m)\gamma(\Sigma,N,m)\Big(\frac{2X}{N^{2}m^{2}} + O(1)\Big)^{n+1}+ O_\epsilon\Big(\frac{X^{n+1+\xi_n+\epsilon}}{M^{\delta_n}}+X^{n+1-{\eta_n}+\epsilon}\Big)\\[-.025in]\nonumber&=\sum_{\substack{(m,N)=1\\m\leq M}}\Biggl( (2X)^{n+1}\mu(m)\prod_{p\mid m}\Big(\frac{\#\Sigma_p}{p^{2n+2}} - \alpha_n(\Sigma,p)\Big) + O\Big(N^2X^{n}m^\epsilon+N^{2n+2}m^{2n+\epsilon}\Big)\Biggr)\\& \nonumber \quad +\,O_\epsilon\Big(\frac{X^{n+1+\xi_n+\epsilon}}{M^{\delta_n}}+X^{n+1-{\eta_n}+\epsilon}\Big)\\\nonumber&= (2X)^{n+1}\alpha_n(\Sigma) + O\Big(\frac{X^{n+1}}{M^{1-\epsilon}} + N^2M^{1+\epsilon}X^n + N^{2n+2}M^{2n+1+\epsilon} + \frac{X^{n+1+\xi_n+\epsilon}}{M^{\delta_n}}+X^{n+1-{\eta_n}+\epsilon}\Big). \end{align*} $$
$$ \begin{align*} \nonumber&\#\{f\in V_n(\Sigma)\colon H(f)<X\text{ and } \Delta(f)\text{ squarefree}\}\\[.025in]\nonumber &=\sum_{\substack{(m,N)=1\\m\leq M}} \mu(m)\#\{f\in {\mathcal{W}}_m(\Sigma)\colon H(f)<X\} + O_\epsilon\Big(\frac{X^{n+1+\xi_n+\epsilon}}{M^{\delta_n}}+X^{n+1-{\eta_n}+\epsilon}\Big)\\[-.025in]\nonumber&=\sum_{\substack{(m,N)=1\\m\leq M}} \mu(m)\gamma(\Sigma,N,m)\Big(\frac{2X}{N^{2}m^{2}} + O(1)\Big)^{n+1}+ O_\epsilon\Big(\frac{X^{n+1+\xi_n+\epsilon}}{M^{\delta_n}}+X^{n+1-{\eta_n}+\epsilon}\Big)\\[-.025in]\nonumber&=\sum_{\substack{(m,N)=1\\m\leq M}}\Biggl( (2X)^{n+1}\mu(m)\prod_{p\mid m}\Big(\frac{\#\Sigma_p}{p^{2n+2}} - \alpha_n(\Sigma,p)\Big) + O\Big(N^2X^{n}m^\epsilon+N^{2n+2}m^{2n+\epsilon}\Big)\Biggr)\\& \nonumber \quad +\,O_\epsilon\Big(\frac{X^{n+1+\xi_n+\epsilon}}{M^{\delta_n}}+X^{n+1-{\eta_n}+\epsilon}\Big)\\\nonumber&= (2X)^{n+1}\alpha_n(\Sigma) + O\Big(\frac{X^{n+1}}{M^{1-\epsilon}} + N^2M^{1+\epsilon}X^n + N^{2n+2}M^{2n+1+\epsilon} + \frac{X^{n+1+\xi_n+\epsilon}}{M^{\delta_n}}+X^{n+1-{\eta_n}+\epsilon}\Big). \end{align*} $$
Recalling that
![]() $\delta _n = 1/2$
or
$\delta _n = 1/2$
or
![]() $1/3$
, we may take
$1/3$
, we may take
![]() $M = X^{3\eta _n+3\xi _n}$
to obtain the first claim in Theorem 7.1. The second claim follows identically.
$M = X^{3\eta _n+3\xi _n}$
to obtain the first claim in Theorem 7.1. The second claim follows identically.
Taking
![]() $N=1$
in Theorem 7.1 yields Theorem 6. Theorems 1 and 2 are then immediate consequences of Theorem 6.
$N=1$
in Theorem 7.1 yields Theorem 6. Theorems 1 and 2 are then immediate consequences of Theorem 6.
Next, we prove lower bounds on the number of
![]() $S_n$
-fields having bounded discriminant. Let
$S_n$
-fields having bounded discriminant. Let
![]() $f(x,y) = a_0x^n + a_1x^{n-1}y + \cdots + a_ny^n$
be a real binary n-ic form with
$f(x,y) = a_0x^n + a_1x^{n-1}y + \cdots + a_ny^n$
be a real binary n-ic form with
![]() $a_0\neq 0$
and nonzero discriminant. Let
$a_0\neq 0$
and nonzero discriminant. Let
![]() $\theta $
be the image of x in
$\theta $
be the image of x in
![]() ${\mathbb {R}}[x]/(f(x,1))$
, and write
${\mathbb {R}}[x]/(f(x,1))$
, and write
![]() $R_f$
for the lattice spanned by
$R_f$
for the lattice spanned by
in
![]() ${\mathbb {R}}[x]/(f(x,1))$
. Here, we identify
${\mathbb {R}}[x]/(f(x,1))$
. Here, we identify
![]() ${\mathbb {R}}[x]/(f(x,1))$
with
${\mathbb {R}}[x]/(f(x,1))$
with
![]() ${\mathbb {R}}^n$
via its real and complex embeddings and by identifying
${\mathbb {R}}^n$
via its real and complex embeddings and by identifying
![]() ${\mathbb {C}}={\mathbb {R}}\oplus i{\mathbb {R}}$
with
${\mathbb {C}}={\mathbb {R}}\oplus i{\mathbb {R}}$
with
![]() ${\mathbb {R}}^2$
.
${\mathbb {R}}^2$
.
We say that
![]() $f(x,y)$
is Minkowski-reduced if the basis
$f(x,y)$
is Minkowski-reduced if the basis
![]() $\{1,\zeta _1,\ldots ,\zeta _{n-1}\}$
of
$\{1,\zeta _1,\ldots ,\zeta _{n-1}\}$
of
![]() $R_f$
is Minkowski-reduced. We say that
$R_f$
is Minkowski-reduced. We say that
![]() $f(x,y)$
, or its
$f(x,y)$
, or its
![]() $\mathrm {{SL}}_2({\mathbb {Z}})$
-orbit, is quasi-reduced if there exists
$\mathrm {{SL}}_2({\mathbb {Z}})$
-orbit, is quasi-reduced if there exists
![]() $\gamma \in \mathrm {{SL}}_2({\mathbb {Z}})$
such that
$\gamma \in \mathrm {{SL}}_2({\mathbb {Z}})$
such that
![]() $\gamma .f$
is Minkowski-reduced. We add the prefix ‘strongly’ if the relevant lattice has a unique Minkowski-reduced basis. The relevance of being strongly quasi-reduced is contained in the following lemma.
$\gamma .f$
is Minkowski-reduced. We add the prefix ‘strongly’ if the relevant lattice has a unique Minkowski-reduced basis. The relevance of being strongly quasi-reduced is contained in the following lemma.
Lemma 7.2. Let
![]() $n\geq 3$
and let
$n\geq 3$
and let
![]() $f(x,y)$
and
$f(x,y)$
and
![]() $f^*(x,y)$
be strongly quasi-reduced integral binary n-ic forms. Suppose the corresponding rank-n rings
$f^*(x,y)$
be strongly quasi-reduced integral binary n-ic forms. Suppose the corresponding rank-n rings
![]() $R_f$
and
$R_f$
and
![]() $R_{f^*}$
are isomorphic. Then
$R_{f^*}$
are isomorphic. Then
![]() $f(x,y)$
and
$f(x,y)$
and
![]() $f^*(x,y)$
are
$f^*(x,y)$
are
![]() $\mathrm {{SL}}_2({\mathbb {Z}})$
-equivalent.
$\mathrm {{SL}}_2({\mathbb {Z}})$
-equivalent.
Proof. It suffices to assume
![]() $f(x,y)=a_0x^n + \cdots + a_ny^n$
and
$f(x,y)=a_0x^n + \cdots + a_ny^n$
and
![]() $f^*(x,y) = a_0^*x^n + \cdots + a_n^*y^n$
are strongly Minkowski-reduced with
$f^*(x,y) = a_0^*x^n + \cdots + a_n^*y^n$
are strongly Minkowski-reduced with
![]() $R_f\simeq R_{f^*}$
. We show
$R_f\simeq R_{f^*}$
. We show
![]() $f(x,y) = f^*(x,y)$
. Let
$f(x,y) = f^*(x,y)$
. Let
![]() $\phi :R_f\rightarrow R_{f^*}$
be a ring isomorphism. By the uniqueness of Minkowski-reduced bases,
$\phi :R_f\rightarrow R_{f^*}$
be a ring isomorphism. By the uniqueness of Minkowski-reduced bases,
![]() $\phi $
must map the basis elements
$\phi $
must map the basis elements
![]() $1,\zeta _1,\ldots ,\zeta _{n-1}$
for
$1,\zeta _1,\ldots ,\zeta _{n-1}$
for
![]() $R_f$
to the corresponding basis elements
$R_f$
to the corresponding basis elements
![]() $1,\zeta ^*_1,\ldots ,\zeta ^*_{n-1}$
for
$1,\zeta ^*_1,\ldots ,\zeta ^*_{n-1}$
for
![]() $R_{f^*}$
. Let
$R_{f^*}$
. Let
![]() $\theta $
denote the image of x in
$\theta $
denote the image of x in
![]() ${\mathbb {Q}}[x]/(f(x,1))$
and
${\mathbb {Q}}[x]/(f(x,1))$
and
![]() $\theta ^*$
the image of x in
$\theta ^*$
the image of x in
![]() ${\mathbb {Q}}[x]/(f^*(x,1))$
. Then
${\mathbb {Q}}[x]/(f^*(x,1))$
. Then
![]() $\phi (a_0\theta ) = a_0^*\theta ^*$
and
$\phi (a_0\theta ) = a_0^*\theta ^*$
and
Since
![]() $\theta ^*$
and
$\theta ^*$
and
![]() $\theta ^{*2}$
are linearly independent, we have
$\theta ^{*2}$
are linearly independent, we have
![]() $a_0 = a_0^*$
,
$a_0 = a_0^*$
,
![]() $a_1 = a_1^*$
, and
$a_1 = a_1^*$
, and
![]() $\phi (\theta ) = \theta ^*$
, where we extend
$\phi (\theta ) = \theta ^*$
, where we extend
![]() $\phi $
naturally to
$\phi $
naturally to
![]() $R_f\otimes {\mathbb {Q}} = {\mathbb {Q}}[x]/(f(x,1))$
. Then since
$R_f\otimes {\mathbb {Q}} = {\mathbb {Q}}[x]/(f(x,1))$
. Then since
![]() $\phi (\zeta _{n-1}) = \zeta ^*_{n-1}$
, we have
$\phi (\zeta _{n-1}) = \zeta ^*_{n-1}$
, we have
![]() $a_i=a_i^*$
for
$a_i=a_i^*$
for
![]() $i=0,\ldots ,n-2$
. Finally,
$i=0,\ldots ,n-2$
. Finally,
![]() $\phi (-a_{n-1}\theta - a_n) = \phi (\theta \zeta _{n-1}) =\phi (\theta ^*\zeta _{n-1}^*)= -a_{n-1}^*\theta ^* - a_n^*$
. Hence,
$\phi (-a_{n-1}\theta - a_n) = \phi (\theta \zeta _{n-1}) =\phi (\theta ^*\zeta _{n-1}^*)= -a_{n-1}^*\theta ^* - a_n^*$
. Hence,
![]() $a_{n-1} = a^*_{n-1}$
and
$a_{n-1} = a^*_{n-1}$
and
![]() $a_n = a^*_n$
.
$a_n = a^*_n$
.
Proof of Theorem 3.
The condition of being strongly quasi-reduced is open in
![]() $V_n({\mathbb {R}})$
. Therefore, given a strongly quasi-reduced element
$V_n({\mathbb {R}})$
. Therefore, given a strongly quasi-reduced element
![]() $f\in V_n({\mathbb {R}})$
, there exists an open neighbourhood
$f\in V_n({\mathbb {R}})$
, there exists an open neighbourhood
![]() ${\mathcal {B}}$
of f in which every element is strongly quasi-reduced. Moreover, since the action of
${\mathcal {B}}$
of f in which every element is strongly quasi-reduced. Moreover, since the action of
![]() $\mathrm {{SL}}_2({\mathbb {Z}})$
on
$\mathrm {{SL}}_2({\mathbb {Z}})$
on
![]() $V_n({\mathbb {R}})$
is discrete, we may ensure that no two elements of
$V_n({\mathbb {R}})$
is discrete, we may ensure that no two elements of
![]() ${\mathcal {B}}$
are
${\mathcal {B}}$
are
![]() $\mathrm {{SL}}_2({\mathbb {Z}})$
-equivalent. We may further scale
$\mathrm {{SL}}_2({\mathbb {Z}})$
-equivalent. We may further scale
![]() ${\mathcal {B}}$
in order to assume that every element in
${\mathcal {B}}$
in order to assume that every element in
![]() ${\mathcal {B}}$
has discriminant bounded by
${\mathcal {B}}$
has discriminant bounded by
![]() $1$
.
$1$
.
Consider the set
![]() ${\mathcal {B}}_X:=X^{1/(2n-2)}\cdot {\mathcal {B}}$
. No two elements in it are
${\mathcal {B}}_X:=X^{1/(2n-2)}\cdot {\mathcal {B}}$
. No two elements in it are
![]() $\mathrm {{SL}}_2({\mathbb {Z}})$
-equivalent, and every element in it is strongly quasi-reduced. Therefore, the rings corresponding to any two elements in
$\mathrm {{SL}}_2({\mathbb {Z}})$
-equivalent, and every element in it is strongly quasi-reduced. Therefore, the rings corresponding to any two elements in
![]() ${\mathcal {B}}_X$
are nonisomorphic. However, applying Theorem 7.1, we see that
${\mathcal {B}}_X$
are nonisomorphic. However, applying Theorem 7.1, we see that
![]() $\gg X^{(n+1)/(2n-2)}$
integral elements in
$\gg X^{(n+1)/(2n-2)}$
integral elements in
![]() ${\mathcal {B}}_X$
have discriminant less than X and correspond to maximal orders in degree-n number fields. Since these rings are pairwise nonisomorphic, so are their fields of fractions. Hence, we have constructed
${\mathcal {B}}_X$
have discriminant less than X and correspond to maximal orders in degree-n number fields. Since these rings are pairwise nonisomorphic, so are their fields of fractions. Hence, we have constructed
![]() $\gg X^{(n+1)/(2n-2)}$
nonisomorphic degree-n number fields of absolute discriminant less than X. Restricting to counting forms that have squarefree discriminant yields
$\gg X^{(n+1)/(2n-2)}$
nonisomorphic degree-n number fields of absolute discriminant less than X. Restricting to counting forms that have squarefree discriminant yields
![]() $\gg X^{(n+1)/(2n-2)}$
nonisomorphic
$\gg X^{(n+1)/(2n-2)}$
nonisomorphic
![]() $S_n$
-number fields.
$S_n$
-number fields.
We note that Theorem 7.1 also allows us to construct
![]() $\gg X^{(n+1)/(2n-2)} S_n$
-number fields satisfying any finite set of splitting conditions.
$\gg X^{(n+1)/(2n-2)} S_n$
-number fields satisfying any finite set of splitting conditions.
A Computations of the local densities
 $\alpha _n(p),\beta _n(p)$
$\alpha _n(p),\beta _n(p)$
Let
![]() $n\geq 2$
be a fixed integer. For a prime p, let
$n\geq 2$
be a fixed integer. For a prime p, let
![]() $\alpha _n(p)$
denote the density of the set of binary n-ic forms having discriminant indivisible by
$\alpha _n(p)$
denote the density of the set of binary n-ic forms having discriminant indivisible by
![]() $p^2$
, and let
$p^2$
, and let
![]() $\beta _n(p)$
denote the density of binary n-ic forms whose associated rank-n rings are maximal at p. In this section, we compute
$\beta _n(p)$
denote the density of binary n-ic forms whose associated rank-n rings are maximal at p. In this section, we compute
![]() $\alpha _n(p)$
and
$\alpha _n(p)$
and
![]() $\beta _n(p)$
for all integers
$\beta _n(p)$
for all integers
![]() $n\geq 2$
and all primes p.
$n\geq 2$
and all primes p.
Proposition A.1. We have
![]() $\alpha _2(2) = 1/2$
and
$\alpha _2(2) = 1/2$
and
![]() $\alpha _n(2) = 3/8$
for
$\alpha _n(2) = 3/8$
for
![]() $n\geq 3$
. For odd primes p, we have
$n\geq 3$
. For odd primes p, we have
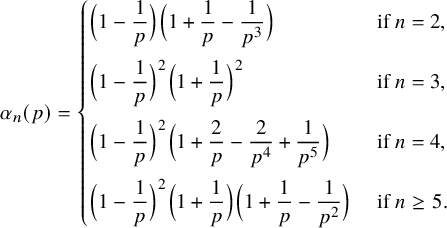 $$ \begin{align*}\alpha_n(p) = \begin{cases}\displaystyle \Big(1-\frac{1}{p}\Big) \Big(1+\frac{1}{p}-\frac{1}{p^3}\Big) &\text{ if }n=2, \\[.15in] \displaystyle\Big(1-\frac{1}{p}\Big)^2\Big(1+\frac{1}{p}\Big)^2 &\text{ if }n=3, \\[.15in] \displaystyle\Big(1-\frac{1}{p}\Big)^2 \Big(1+\frac{2}{p}-\frac{2}{p^4}+\frac{1}{p^5}\Big) &\text{ if }n=4, \\[.15in] \displaystyle\Big(1-\frac{1}{p}\Big)^2 \Big(1+\frac{1}{p}\Big)\Big(1+\frac{1}{p}-\frac{1}{p^2}\Big) &\text{ if }n\geq5.\end{cases}\end{align*} $$
$$ \begin{align*}\alpha_n(p) = \begin{cases}\displaystyle \Big(1-\frac{1}{p}\Big) \Big(1+\frac{1}{p}-\frac{1}{p^3}\Big) &\text{ if }n=2, \\[.15in] \displaystyle\Big(1-\frac{1}{p}\Big)^2\Big(1+\frac{1}{p}\Big)^2 &\text{ if }n=3, \\[.15in] \displaystyle\Big(1-\frac{1}{p}\Big)^2 \Big(1+\frac{2}{p}-\frac{2}{p^4}+\frac{1}{p^5}\Big) &\text{ if }n=4, \\[.15in] \displaystyle\Big(1-\frac{1}{p}\Big)^2 \Big(1+\frac{1}{p}\Big)\Big(1+\frac{1}{p}-\frac{1}{p^2}\Big) &\text{ if }n\geq5.\end{cases}\end{align*} $$
Proof. For
![]() $j\geq 0$
,
$j\geq 0$
,
![]() $n\geq 1$
, and p prime, we let
$n\geq 1$
, and p prime, we let
![]() $\nu _{j}(n,p)$
denote the density within monic degree-n integer polynomials of the set of those whose discriminants have p-adic valuation j. Then
$\nu _{j}(n,p)$
denote the density within monic degree-n integer polynomials of the set of those whose discriminants have p-adic valuation j. Then
![]() $\nu _0(n,p)$
and
$\nu _0(n,p)$
and
![]() $\nu _1(n,p)$
are computed in [Reference Ash, Brakenhoff and Zarrabi2, Proposition 6.4 and Theorem 6.8]:
$\nu _1(n,p)$
are computed in [Reference Ash, Brakenhoff and Zarrabi2, Proposition 6.4 and Theorem 6.8]:
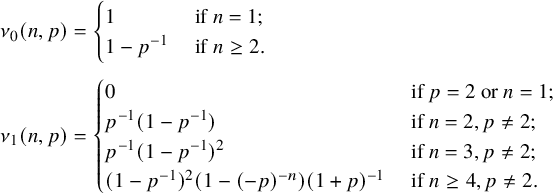 $$ \begin{align*} \nonumber \nu_0(n,p) &= \begin{cases}1&\text{ if }n= 1;\\ 1-p^{-1}&\text{ if }n\geq 2.\end{cases}\\[.035in] \nonumber\nu_1(n,p) &= \begin{cases}0&\text{ if }p=2 \text{ or }n= 1;\\ p^{-1}(1-p^{-1})&\text{ if }n=2,p\neq2;\\ p^{-1}(1-p^{-1})^2&\text{ if }n=3,p\neq2;\\ (1-p^{-1})^2(1-(-p)^{-n})(1+p)^{-1}&\text{ if }n\geq4,p\neq2. \end{cases} \end{align*} $$
$$ \begin{align*} \nonumber \nu_0(n,p) &= \begin{cases}1&\text{ if }n= 1;\\ 1-p^{-1}&\text{ if }n\geq 2.\end{cases}\\[.035in] \nonumber\nu_1(n,p) &= \begin{cases}0&\text{ if }p=2 \text{ or }n= 1;\\ p^{-1}(1-p^{-1})&\text{ if }n=2,p\neq2;\\ p^{-1}(1-p^{-1})^2&\text{ if }n=3,p\neq2;\\ (1-p^{-1})^2(1-(-p)^{-n})(1+p)^{-1}&\text{ if }n\geq4,p\neq2. \end{cases} \end{align*} $$
To compute the densities
![]() $\alpha _n(p)$
, we partition the set of integral binary n-ic forms
$\alpha _n(p)$
, we partition the set of integral binary n-ic forms
![]() $f(x,y)=a_0x^n+a_1x^{n-1}y+\cdots +a_ny^n$
whose discriminants are not divisible by
$f(x,y)=a_0x^n+a_1x^{n-1}y+\cdots +a_ny^n$
whose discriminants are not divisible by
![]() $p^2$
into three subsets, and compute each of their densities. For any binary form
$p^2$
into three subsets, and compute each of their densities. For any binary form
![]() $f(x,y)$
in
$f(x,y)$
in
![]() ${\mathbb {Z}}[x,y]$
or in
${\mathbb {Z}}[x,y]$
or in
![]() $({\mathbb {Z}}/p^2{\mathbb {Z}})[x,y]$
, we write
$({\mathbb {Z}}/p^2{\mathbb {Z}})[x,y]$
, we write
![]() $\bar {f}(x,y)$
for its reduction modulo p.
$\bar {f}(x,y)$
for its reduction modulo p.
Subset 1: The set of
![]() $f(x,y)$
with
$f(x,y)$
with
![]() $p\nmid a_0$
and
$p\nmid a_0$
and
![]() $p^2\nmid \Delta (f)$
. Here, for any fixed leading coefficient
$p^2\nmid \Delta (f)$
. Here, for any fixed leading coefficient
![]() $a_0\not \equiv 0\pmod p$
, the density of
$a_0\not \equiv 0\pmod p$
, the density of
![]() $f(x,y)$
having discriminant indivisible by
$f(x,y)$
having discriminant indivisible by
![]() $p^2$
is simply given by
$p^2$
is simply given by
![]() $\nu _0(n,p)+\nu _1(n,p)$
. Therefore, the p-adic density of this subset is equal to
$\nu _0(n,p)+\nu _1(n,p)$
. Therefore, the p-adic density of this subset is equal to
Subset 2: The set of
![]() $f(x,y)$
with
$f(x,y)$
with
![]() $p\mid a_0$
,
$p\mid a_0$
,
![]() $p\nmid a_1$
, and
$p\nmid a_1$
, and
![]() $p^2\nmid \Delta (f)$
. In this case, we begin by proving that the density of elements f with fixed
$p^2\nmid \Delta (f)$
. In this case, we begin by proving that the density of elements f with fixed
![]() $a_0$
and
$a_0$
and
![]() $a_1$
and with
$a_1$
and with
![]() $p^2\nmid \Delta (f)$
is the same as the density of binary
$p^2\nmid \Delta (f)$
is the same as the density of binary
![]() $(n-1)$
-ic forms g, with fixed leading coefficient
$(n-1)$
-ic forms g, with fixed leading coefficient
![]() $a_1$
such that
$a_1$
such that
![]() $p^2\nmid \Delta (g)$
. Indeed, given any
$p^2\nmid \Delta (g)$
. Indeed, given any
![]() $(a_2,\ldots ,a_n)\in ({\mathbb {Z}}/p^2{\mathbb {Z}})^{n-1}$
, we write
$(a_2,\ldots ,a_n)\in ({\mathbb {Z}}/p^2{\mathbb {Z}})^{n-1}$
, we write
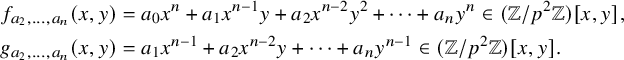 $$ \begin{align*} f_{a_2,\ldots,a_n}(x,y) &= a_0x^n + a_1x^{n-1}y + a_2x^{n-2}y^2 + \cdots + a_ny^n\in({\mathbb{Z}}/p^2{\mathbb{Z}})[x,y],\\g_{a_2,\ldots,a_n}(x,y) &= a_1x^{n-1} + a_2x^{n-2}y + \cdots + a_ny^{n-1}\in({\mathbb{Z}}/p^2{\mathbb{Z}})[x,y]. \end{align*} $$
$$ \begin{align*} f_{a_2,\ldots,a_n}(x,y) &= a_0x^n + a_1x^{n-1}y + a_2x^{n-2}y^2 + \cdots + a_ny^n\in({\mathbb{Z}}/p^2{\mathbb{Z}})[x,y],\\g_{a_2,\ldots,a_n}(x,y) &= a_1x^{n-1} + a_2x^{n-2}y + \cdots + a_ny^{n-1}\in({\mathbb{Z}}/p^2{\mathbb{Z}})[x,y]. \end{align*} $$
Define
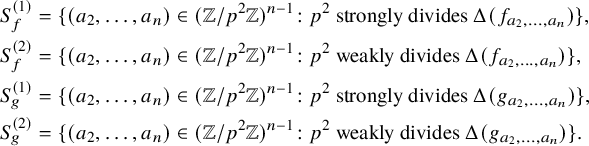 $$ \begin{align*} \nonumber S_f^{(1)} &= \{(a_2,\ldots,a_n)\in({\mathbb{Z}}/p^2{\mathbb{Z}})^{n-1} \colon p^2 \text{ strongly divides }\Delta(f_{a_2,\ldots,a_n})\},\\ \nonumber S_f^{(2)} &= \{(a_2,\ldots,a_n)\in({\mathbb{Z}}/p^2{\mathbb{Z}})^{n-1} \colon p^2 \text{ weakly divides }\Delta(f_{a_2,\ldots,a_n})\},\\ \nonumber S_g^{(1)} &= \{(a_2,\ldots,a_n)\in({\mathbb{Z}}/p^2{\mathbb{Z}})^{n-1} \colon p^2 \text{ strongly divides }\Delta(g_{a_2,\ldots,a_n})\},\\ \nonumber S_g^{(2)} &= \{(a_2,\ldots,a_n)\in({\mathbb{Z}}/p^2{\mathbb{Z}})^{n-1} \colon p^2 \text{ weakly divides }\Delta(g_{a_2,\ldots,a_n})\}. \end{align*} $$
$$ \begin{align*} \nonumber S_f^{(1)} &= \{(a_2,\ldots,a_n)\in({\mathbb{Z}}/p^2{\mathbb{Z}})^{n-1} \colon p^2 \text{ strongly divides }\Delta(f_{a_2,\ldots,a_n})\},\\ \nonumber S_f^{(2)} &= \{(a_2,\ldots,a_n)\in({\mathbb{Z}}/p^2{\mathbb{Z}})^{n-1} \colon p^2 \text{ weakly divides }\Delta(f_{a_2,\ldots,a_n})\},\\ \nonumber S_g^{(1)} &= \{(a_2,\ldots,a_n)\in({\mathbb{Z}}/p^2{\mathbb{Z}})^{n-1} \colon p^2 \text{ strongly divides }\Delta(g_{a_2,\ldots,a_n})\},\\ \nonumber S_g^{(2)} &= \{(a_2,\ldots,a_n)\in({\mathbb{Z}}/p^2{\mathbb{Z}})^{n-1} \colon p^2 \text{ weakly divides }\Delta(g_{a_2,\ldots,a_n})\}. \end{align*} $$
Recall that
![]() $p^2$
strongly divides the discriminant of f if and only if
$p^2$
strongly divides the discriminant of f if and only if
![]() $\bar {f}(x,y)$
has a factor of the form
$\bar {f}(x,y)$
has a factor of the form
![]() $h(x,y)^3$
for some linear form h or a factor of the form
$h(x,y)^3$
for some linear form h or a factor of the form
![]() $j(x,y)^2$
where j is a binary form of degree at least 2. Since
$j(x,y)^2$
where j is a binary form of degree at least 2. Since
![]() $\overline {f_{a_2,\ldots ,a_n}}(x,y)\equiv y\,\overline {g_{a_2,\ldots ,a_n}}(x,y)$
, and since y does not divide
$\overline {f_{a_2,\ldots ,a_n}}(x,y)\equiv y\,\overline {g_{a_2,\ldots ,a_n}}(x,y)$
, and since y does not divide
![]() $\overline {g_{a_2,\ldots ,a_n}}(x,y)$
, we see that
$\overline {g_{a_2,\ldots ,a_n}}(x,y)$
, we see that
![]() $\overline {f_{a_2,\ldots ,a_n}}(x,y)$
admits such a factor if and only if
$\overline {f_{a_2,\ldots ,a_n}}(x,y)$
admits such a factor if and only if
![]() $\overline {g_{a_2,\ldots ,a_n}}(x,y)$
does. Hence,
$\overline {g_{a_2,\ldots ,a_n}}(x,y)$
does. Hence,
![]() $S_f^{(1)} = S_g^{(1)}$
. However, we have
$S_f^{(1)} = S_g^{(1)}$
. However, we have
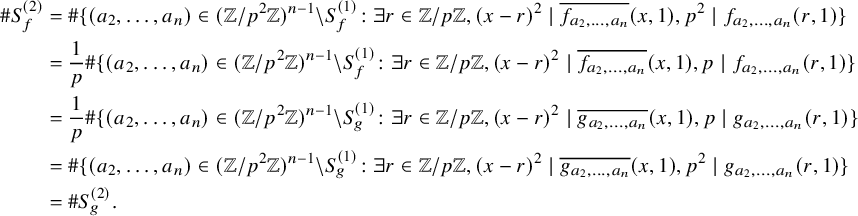 $$ \begin{align*} \nonumber\#S_f^{(2)} &= \#\{(a_2,\ldots,a_n)\in({\mathbb{Z}}/p^2{\mathbb{Z}})^{n-1}\backslash S_f^{(1)} \colon \exists r\in{\mathbb{Z}}/p{\mathbb{Z}}, (x-r)^2\mid \overline{f_{a_2,\ldots,a_n}}(x,1), p^2\mid f_{a_2,\ldots,a_n}(r,1)\}\\ \nonumber&= \frac{1}{p}\#\{(a_2,\ldots,a_n)\in({\mathbb{Z}}/p^2{\mathbb{Z}})^{n-1}\backslash S_f^{(1)} \colon \exists r\in{\mathbb{Z}}/p{\mathbb{Z}}, (x-r)^2\mid \overline{f_{a_2,\ldots,a_n}}(x,1), p\mid f_{a_2,\ldots,a_n}(r,1)\}\\ \nonumber&= \frac{1}{p}\#\{(a_2,\ldots,a_n)\in({\mathbb{Z}}/p^2{\mathbb{Z}})^{n-1}\backslash S_g^{(1)} \colon \exists r\in{\mathbb{Z}}/p{\mathbb{Z}}, (x-r)^2\mid \overline{g_{a_2,\ldots,a_n}}(x,1), p\mid g_{a_2,\ldots,a_n}(r,1)\}\\ \nonumber&= \#\{(a_2,\ldots,a_n)\in({\mathbb{Z}}/p^2{\mathbb{Z}})^{n-1}\backslash S_g^{(1)} \colon \exists r\in{\mathbb{Z}}/p{\mathbb{Z}}, (x-r)^2\mid \overline{g_{a_2,\ldots,a_n}}(x,1), p^2\mid g_{a_2,\ldots,a_n}(r,1)\}\\ &= \#S_g^{(2)}. \end{align*} $$
$$ \begin{align*} \nonumber\#S_f^{(2)} &= \#\{(a_2,\ldots,a_n)\in({\mathbb{Z}}/p^2{\mathbb{Z}})^{n-1}\backslash S_f^{(1)} \colon \exists r\in{\mathbb{Z}}/p{\mathbb{Z}}, (x-r)^2\mid \overline{f_{a_2,\ldots,a_n}}(x,1), p^2\mid f_{a_2,\ldots,a_n}(r,1)\}\\ \nonumber&= \frac{1}{p}\#\{(a_2,\ldots,a_n)\in({\mathbb{Z}}/p^2{\mathbb{Z}})^{n-1}\backslash S_f^{(1)} \colon \exists r\in{\mathbb{Z}}/p{\mathbb{Z}}, (x-r)^2\mid \overline{f_{a_2,\ldots,a_n}}(x,1), p\mid f_{a_2,\ldots,a_n}(r,1)\}\\ \nonumber&= \frac{1}{p}\#\{(a_2,\ldots,a_n)\in({\mathbb{Z}}/p^2{\mathbb{Z}})^{n-1}\backslash S_g^{(1)} \colon \exists r\in{\mathbb{Z}}/p{\mathbb{Z}}, (x-r)^2\mid \overline{g_{a_2,\ldots,a_n}}(x,1), p\mid g_{a_2,\ldots,a_n}(r,1)\}\\ \nonumber&= \#\{(a_2,\ldots,a_n)\in({\mathbb{Z}}/p^2{\mathbb{Z}})^{n-1}\backslash S_g^{(1)} \colon \exists r\in{\mathbb{Z}}/p{\mathbb{Z}}, (x-r)^2\mid \overline{g_{a_2,\ldots,a_n}}(x,1), p^2\mid g_{a_2,\ldots,a_n}(r,1)\}\\ &= \#S_g^{(2)}. \end{align*} $$
The density
![]() $(\#S_g^{(1)}+\#S_g^{(2)})/p^{2(n-1)}$
is
$(\#S_g^{(1)}+\#S_g^{(2)})/p^{2(n-1)}$
is
![]() $\nu _0(n-1,p)+\nu _1(n-1,p)$
. Taking into account that
$\nu _0(n-1,p)+\nu _1(n-1,p)$
. Taking into account that
![]() $p\mid a_0$
and
$p\mid a_0$
and
![]() $p\nmid a_1$
, we see that the density of this second subset is
$p\nmid a_1$
, we see that the density of this second subset is
Subset 3: The set of
![]() $f(x,y)$
with
$f(x,y)$
with
![]() $p\mid a_0$
,
$p\mid a_0$
,
![]() $p\mid a_1$
, and
$p\mid a_1$
, and
![]() $p^2\nmid \Delta (f)$
. Note that we already have
$p^2\nmid \Delta (f)$
. Note that we already have
![]() $p\mid \Delta (f)$
in this case. To ensure that
$p\mid \Delta (f)$
in this case. To ensure that
![]() $p^2\nmid \Delta (f)$
, we must have
$p^2\nmid \Delta (f)$
, we must have
![]() $p>2$
,
$p>2$
,
![]() $p^2\nmid a_0$
, and
$p^2\nmid a_0$
, and
![]() $p\nmid a_2$
. Indeed, if
$p\nmid a_2$
. Indeed, if
![]() $p=2$
, then since
$p=2$
, then since
![]() $2\mid \Delta (f)$
, we have
$2\mid \Delta (f)$
, we have
![]() $4\mid \Delta (f)$
; if
$4\mid \Delta (f)$
; if
![]() $p^2\mid a_0$
, then
$p^2\mid a_0$
, then
![]() $p^2$
(weakly) divides
$p^2$
(weakly) divides
![]() $\Delta (f)$
; and if
$\Delta (f)$
; and if
![]() $p\mid a_2$
, then
$p\mid a_2$
, then
![]() $y^3\mid \bar {f}$
and so
$y^3\mid \bar {f}$
and so
![]() $p^2$
(strongly) divides
$p^2$
(strongly) divides
![]() $\Delta (f)$
. As polynomials in
$\Delta (f)$
. As polynomials in
![]() $a_0,\ldots ,a_n$
, we have
$a_0,\ldots ,a_n$
, we have
Hence, if
![]() $p>2$
,
$p>2$
,
![]() $p^2\nmid a_0$
, and
$p^2\nmid a_0$
, and
![]() $p\nmid a_2$
, then
$p\nmid a_2$
, then
![]() $p^2\nmid \Delta (f)$
if and only if
$p^2\nmid \Delta (f)$
if and only if
![]() $p\nmid \Delta (a_2x^{n-2}+a_3x^{n-3}y+\cdots a_ny^{n-2})$
. Hence, the density of this third subset is
$p\nmid \Delta (a_2x^{n-2}+a_3x^{n-3}y+\cdots a_ny^{n-2})$
. Hence, the density of this third subset is
Adding together these three densities yields the proposition.
Next, we compute the value of
![]() $\beta _n(p)$
for integers
$\beta _n(p)$
for integers
![]() $n\geq 2$
and primes p.
$n\geq 2$
and primes p.
Proposition A.2. We have
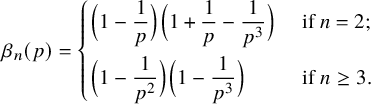 $$ \begin{align*} \beta_n(p) = \begin{cases} \displaystyle\Big(1-\frac{1}{p}\Big)\Big(1+\frac{1}{p}-\frac{1}{p^3}\Big)&\text{ if }n=2; \\[.125in] \displaystyle\Big(1-\frac{1}{p^2}\Big)\Big(1-\frac{1}{p^3}\Big) &\text{ if }n\geq3.\end{cases} \end{align*} $$
$$ \begin{align*} \beta_n(p) = \begin{cases} \displaystyle\Big(1-\frac{1}{p}\Big)\Big(1+\frac{1}{p}-\frac{1}{p^3}\Big)&\text{ if }n=2; \\[.125in] \displaystyle\Big(1-\frac{1}{p^2}\Big)\Big(1-\frac{1}{p^3}\Big) &\text{ if }n\geq3.\end{cases} \end{align*} $$
Proof. The density of monic degree-n integer polynomials that are maximal at p was computed in [Reference Ash, Brakenhoff and Zarrabi2, Proposition 3.5] to be
![]() $1-p^{-2}$
for all
$1-p^{-2}$
for all
![]() $n\geq 2$
and all primes p.
$n\geq 2$
and all primes p.
We compute
![]() $\beta _n(p)$
by working over
$\beta _n(p)$
by working over
![]() ${\mathbb {Z}}_p$
. Fix a binary n-ic form
${\mathbb {Z}}_p$
. Fix a binary n-ic form
![]() $f(x,y)\in V_n({\mathbb {Z}}_p)$
. Suppose
$f(x,y)\in V_n({\mathbb {Z}}_p)$
. Suppose
![]() $f(x,y)$
(mod p) factors as
$f(x,y)$
(mod p) factors as
![]() $y^kg(x,y)$
, where
$y^kg(x,y)$
, where
![]() $g(x,y)$
is a binary
$g(x,y)$
is a binary
![]() $(n-k)$
-ic form over
$(n-k)$
-ic form over
![]() ${\mathbb {F}}_p$
with nonzero
${\mathbb {F}}_p$
with nonzero
![]() $x^{n-k}$
-term for some
$x^{n-k}$
-term for some
![]() $k\in \{0,\ldots ,n\}$
. Then, by Hensel’s lemma,
$k\in \{0,\ldots ,n\}$
. Then, by Hensel’s lemma,
![]() $f(x,y)$
factors as
$f(x,y)$
factors as
![]() $h_1(x,y)h_2(x,y)$
where
$h_1(x,y)h_2(x,y)$
where
![]() $h_1(x,y)\in {\mathbb {Z}}_p[x]$
is a binary k-ic form such that
$h_1(x,y)\in {\mathbb {Z}}_p[x]$
is a binary k-ic form such that
![]() $h_1(x,y)$
(mod p) is
$h_1(x,y)$
(mod p) is
![]() $y^k$
and
$y^k$
and
![]() $h_2(x,y)\in {\mathbb {Z}}_p[x]$
is a binary
$h_2(x,y)\in {\mathbb {Z}}_p[x]$
is a binary
![]() $(n-k)$
-ic such that
$(n-k)$
-ic such that
![]() $h_2(x,y)$
(mod p) is
$h_2(x,y)$
(mod p) is
![]() $g(x,y)$
. By scaling
$g(x,y)$
. By scaling
![]() $h_1$
and
$h_1$
and
![]() $h_2$
, we may further assume that the leading coefficient of
$h_2$
, we may further assume that the leading coefficient of
![]() $h_2(x,y)$
is
$h_2(x,y)$
is
![]() $1$
.
$1$
.
Since
![]() $h_1(x,y)$
and
$h_1(x,y)$
and
![]() $h_2(x,y)$
share no common factors (mod p), the rank-n ring over
$h_2(x,y)$
share no common factors (mod p), the rank-n ring over
![]() ${\mathbb {Z}}_p$
associated to
${\mathbb {Z}}_p$
associated to
![]() $f(x,y)$
is isomorphic to the product of the rings associated to
$f(x,y)$
is isomorphic to the product of the rings associated to
![]() $h_1(x,y)$
and
$h_1(x,y)$
and
![]() $h_2(x,y)$
. Since
$h_2(x,y)$
. Since
![]() $h_1(x,y)$
reduces to a unit times
$h_1(x,y)$
reduces to a unit times
![]() $y^k$
modulo p, the rank-k ring associated to
$y^k$
modulo p, the rank-k ring associated to
![]() $h_1(x,y)$
is always maximal when
$h_1(x,y)$
is always maximal when
![]() $k\leq 1$
and is maximal when
$k\leq 1$
and is maximal when
![]() $k\geq 2$
if and only if
$k\geq 2$
if and only if
![]() $p^2$
does not divide the
$p^2$
does not divide the
![]() $x^k$
-coefficient. However,
$x^k$
-coefficient. However,
![]() $h_2(x,y)$
is monic, and so the probability that it is maximal is exactly
$h_2(x,y)$
is monic, and so the probability that it is maximal is exactly
![]() $1-p^{-2}$
when
$1-p^{-2}$
when
![]() $n-k\geq 2$
, and
$n-k\geq 2$
, and
![]() $1$
when
$1$
when
![]() $n-k=1$
. When
$n-k=1$
. When
![]() $k=n$
,
$k=n$
,
![]() $f(x,y)$
is a multiple of p and is automatically nonmaximal. Summing over k, we have for
$f(x,y)$
is a multiple of p and is automatically nonmaximal. Summing over k, we have for
![]() $n\geq 3$
,
$n\geq 3$
,
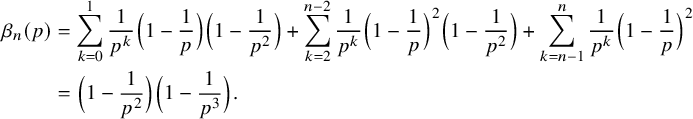 $$ \begin{align*} \nonumber\beta_n(p) &= \sum_{k=0}^1 \frac1{p^k}\Big(1-\frac{1}{p}\Big)\Big(1-\frac{1}{p^2}\Big) + \sum_{k=2}^{n-2} \frac{1}{p^k}\Big(1-\frac{1}{p}\Big)^2 \Big(1-\frac{1}{p^2}\Big) + \sum_{k=n-1}^n \frac{1}{p^{k}}\Big(1-\frac{1}{p}\Big)^2 \\ &= \Big(1-\frac{1}{p^2}\Big)\Big(1-\frac{1}{p^3}\Big). \end{align*} $$
$$ \begin{align*} \nonumber\beta_n(p) &= \sum_{k=0}^1 \frac1{p^k}\Big(1-\frac{1}{p}\Big)\Big(1-\frac{1}{p^2}\Big) + \sum_{k=2}^{n-2} \frac{1}{p^k}\Big(1-\frac{1}{p}\Big)^2 \Big(1-\frac{1}{p^2}\Big) + \sum_{k=n-1}^n \frac{1}{p^{k}}\Big(1-\frac{1}{p}\Big)^2 \\ &= \Big(1-\frac{1}{p^2}\Big)\Big(1-\frac{1}{p^3}\Big). \end{align*} $$
When
![]() $n=2$
, we have
$n=2$
, we have
This concludes the proof of Proposition A.2.
Acknowledgements
We are grateful for comments from the anonymous referees.
Competing interest
The authors have no competing interests to declare.
Funding statement
The first-named author was supported by a Simons Investigator Grant and NSF Grant DMS-1001828. The second-named author was supported by an NSERC Discovery Grant and Sloan Research Fellowship. The third-named author was supported by an NSERC Discovery Grant.