A previously unknown pricing anomaly existed for a few years in the late 1840s in the British government bond market, in which the larger and more liquid of two very large bonds was underpriced. None of the published mechanisms explains this phenomenon. It may be related to another pricing anomaly that existed for much of the nineteenth century in which terminable annuities were significantly underpriced relative to so-called ‘perpetual’ annuities that dominated the government bond market. The reasons for these mispricings seem to lie in the early Victorian culture, since the basic economic incentives as well as laws and institutions were essentially the familiar modern ones. This provides new perspectives on the origins and nature of modern corporate capitalism.

British government bonds formed the deepest, most liquid and most transparent financial market of the nineteenth century. This article shows that those bonds had long periods, extending over decades, of anomalous behavior, in which Consols, the largest and best known of these instruments, were noticeably overpriced relative to equivalent securities which offered the same interest rate and the same guarantee of payment. This finding and similar ones for other comparable pairs of British gilts appear to provide the most extreme counterexamples documented so far to the Efficient Markets Hypothesis and to the Law of One Price, and point the way to further investigations on the origins and nature of the modern economy.

The number, , of rooted plane binary trees of height ≤ h with n internal nodes is shown to satisfy

uniformly for δ−1(log n)−1/2 ≤ β ≤ δ(log n)1/2, where and δ is a positive constant. An asymptotic formula for is derived for h = cn, where 0 < c < 1. Bounds for are also derived for large and small heights. The methods apply to any simple family of trees, and the general asymptotic results are stated.

Using Feferman-Vaught techniques a condition on the fine spectrum of an admissible class of structures is found which leads to a first-order 0–1 law. The condition presented is best possible in the sense that if it is violated then one can find an admissible class with the same fine spectrum which does not have a first–order 0–1 law.

If the condition is satisfied (and hence we have a first-order 0–1 law) we give a natural model of the limit law theory; and show that the limit law theory is decidable if the theory of the directly indecomposables is decidable. Using asymptotic methods from the partition calculus a useful test is derived to show several admissible classes have a first–order 0–1 law.

The problem of Josephus is the following. We are given two positive integers n, q. There are n places arranged around a circle, and numbered clockwise 1, 2, …, n. Each of n people takes one of the places, then (please excuse this, but we didn't invent the problem!) every qth one is executed, until just one remains. More precisely, the occupant of place q is ‘removed’ first, and in general, if some place j has just been vacated, then the qth one of the places clockwise around from j that are still occupied will be vacated next. One question is this: if you would like to be the last survivor, then into what place should you go initially? We denote the answer to this question by Jq(n). For example, if n = 5 and q = 2, the order of execution is 2, 4, 1, 5, 3, and J2(5) = 3. Other questions have been raised about the problem, and it has an extensive literature (see [1]–[10]). In this paper we deal with the Jq(n)'s.

Given a set of n items with real-valued sizes, the optimum partition problem asks how it can be partitioned into two subsets so that the absolute value of the difference of the sums of the sizes over the two subsets is minimized. We present bounds on the probability distribution of this minimum under the assumption that the sizes are independent random variables drawn from a common distribution. For a large class of distributions, we determine the asymptotic behavior of the median of this minimum, and show that it is exponentially small.

In [1, b.2, VIII, 128] Pólya and Szegö give the following interesting result of A. Cohn:

THEOREM 1. If a prime p is expressed in the decimal system as

then the polynomial 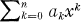irreducible inZ[x].

The proof of this result rests on the following theorem of Pólya and Szegö [1, b.2, VIII, 127] which essentially states that a polynomial f(x) is irreducible if it takes on a prime value at an integer which is sufficiently far from the zeros of f(x).

THEOREM 2. Let f(x) ∊ Z[x] be a polynomial with the zeros α 1, α 2, …, αn . If there is an integer b for which f(b) is a prime, f(b – 1) ≠ 0, and for 1 ≦ i ≦ n, then f(x) is irreducible inZ[x].