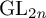 $\mathrm {GL}_{2n}$
OF UNITARY TYPE
$\mathrm {GL}_{2n}$
OF UNITARY TYPE
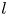 $l$-adic Galois representations, II
$l$-adic Galois representations, II
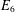 $E_{6}$ AND THE ARITHMETIC OF A FAMILY OF NON-HYPERELLIPTIC CURVES OF GENUS 3
$E_{6}$ AND THE ARITHMETIC OF A FAMILY OF NON-HYPERELLIPTIC CURVES OF GENUS 3
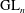 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\text {GL}_{{n}}$
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\text {GL}_{{n}}$