Let n be a positive integer, let 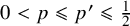$0<p\leqslant p'\leqslant \frac 12$, and let $\ell \leqslant pn$ be a nonnegative integer. We prove that if $\mathcal {F},\mathcal {G}\subseteq \{0,1\}^n$ are two families whose cross intersections forbid 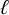$\ell $—that is, they satisfy 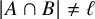$|A\cap B|\neq \ell $ for every 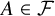$A\in \mathcal {F}$ and every 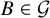$B\in \mathcal {G}$ – then, setting 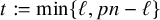$t:= \min \{\ell ,pn-\ell \}$, we have the subgaussian bound

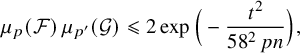$$\begin{align*}\mu_p(\mathcal{F})\, \mu_{p'}(\mathcal{G}) \leqslant 2\exp\Big( - \frac{t^2}{58^2\,pn}\Big), \end{align*}$$

where 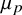$\mu _p$ and 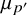$\mu _{p'}$ denote the p-biased and 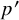$p'$-biased measures on 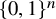$\{0,1\}^n$, respectively.

Let A be a finite set with , let n be a positive integer, and let $A^n$ denote the discrete $n\text {-dimensional}$ hypercube (that is, $A^n$ is the Cartesian product of n many copies of A). Given a family $\langle D_t:t\in A^n\rangle $ of measurable events in a probability space (a stochastic process), what structural information can be obtained assuming that the events $\langle D_t:t\in A^n\rangle $ are not behaving as if they were independent? We obtain an answer to this problem (in a strong quantitative sense) subject to a mild ‘stationarity’ condition. Our result has a number of combinatorial consequences, including a new (and the most informative so far) proof of the density Hales-Jewett theorem.

A tree T is said to be homogeneous if it is uniquely rooted and there exists an integer b ≥ 2, called the branching number of T, such that every t ∈ T has exactly b immediate successors. We study the behaviour of measurable events in probability spaces indexed by homogeneous trees.

Precisely, we show that for every integer b ≥ 2 and every integer n ≥ 1 there exists an integer q(b,n) with the following property. If T is a homogeneous tree with branching number b and {At:t ∈ T} is a family of measurable events in a probability space (Ω,Σ,μ) satisfying μ(At)≥ϵ>0 for every t ∈ T, then for every 0<θ<ϵ there exists a strong subtree S of T of infinite height, such that for every finite subset F of S of cardinality n ≥ 1 we haveIn fact, we can take q(b,n)= ((2b−1)2n−1−1)·(2b−2)−1. A finite version of this result is also obtained.

Let X and Y be separable Banach spaces and denote by 𝒮𝒮(X,Y ) the subset of ℒ(X,Y ) consisting of all strictly singular operators. We study various ordinal ranks on the set 𝒮𝒮(X,Y ). Our main results are summarized as follows. Firstly, we define a new rank r𝒮 on 𝒮𝒮(X,Y ). We show that r𝒮 is a co-analytic rank and that it dominates the rank ϱ introduced by Androulakis, Dodos, Sirotkin and Troitsky [Israel J. Math.169 (2009), 221–250]. Secondly, for every 1≤p<+∞, we construct a Banach space Yp with an unconditional basis such that 𝒮𝒮(ℓp,Yp) is a co-analytic non-Borel subset of ℒ(ℓp,Yp) yet every strictly singular operator T:ℓp→Yp satisfies ϱ(T)≤2. This answers a question of Argyros.

We show that for every separable Banach space $X$ , either $\text{S}{{\text{P}}_{w}}\left( X \right)$ (the set of all spreading models of $X$ generated by weakly-null sequences in $X$ , modulo equivalence) is countable, or $\text{S}{{\text{P}}_{w}}\left( X \right)$ contains an antichain of the size of the continuum. This answers a question of S. J. Dilworth, E. Odell, and B. Sari.

Let ϵ > 0 and be a family of finite subsets of the Cantor set . Following D.H. Fremlin, we say that is ϵ-filling over if is hereditary and for every F ⊆ finite there exists G ⊆ F such that G ϵ and . We show that if is ϵ-filling over and C-measurable in , then for every P ⊆ perfect there exists Q ⊆ P perfect with . A similar result for weaker versions of density is also obtained.

The research presented in this paper was motivated by our aim to study a problem due to J. Bourgain [3]. The problem in question concerns the uniform boundedness of the classical separation rank of the elements of a separable compact set of the first Baire class. In the sequel we shall refer to these sets (separable or non-separable) as Rosenthal compacta and we shall denote by ∝(f) the separation rank of a real-valued function f in B1(X), with X a Polish space. Notice that in [3], Bourgain has provided a positive answer to this problem in the case of K satisfying with X a compact metric space. The key ingredient in Bourgain's approach is that whenever a sequence of continuous functions pointwise converges to a function f, then the possible discontinuities of the limit function reflect a local ℓ1-structure to the sequence (fn)n. More precisely the complexity of this ℓ1-structure increases as the complexity of the discontinuities of f does. This fruitful idea was extensively studied by several authors (c.f. [5], [7], [8]) and for an exposition of the related results we refer to [1]. It is worth mentioning that A.S. Kechris and A. Louveau have invented the rank rND(f) which permits the link between the c0-structure of a sequence (fn)n of uniformly bounded continuous functions and the discontinuities of its pointwise limit. Rosenthal's c0-theorem [11] and the c0-index theorem [2] are consequences of this interaction.

Passing to the case where either (fn)n are not continuous or X is a non-compact Polish space, this nice interaction is completely lost.

The notions of a Baire-1 and a weak Baire-1 multifunction are defined and a striking analogy between Baire-1 multifunctions and classical Baire-1 functions is established. A selection theorem is presented which asserts that if X is a metrisable space, Y a Polish space and F: X → 2Y/{∅} a closed-valued, weak Baire-1 multifunction, then F admits a Baire-1 selection. Using the machinery developed we prove that if X is a Banach space with separable dual, then every weak* usco, defined on a completely metrisable space Z, which values are weakly* compact subsets of the dual, is norm lower semicontinuous on a dense Gδ set.