Let S0,…,Sn be a symmetric random walk that starts at the origin (S0 = 0) and takes steps uniformly distributed on [— 1,+1]. We study the large-n behavior of the expected maximum excursion and prove the estimate
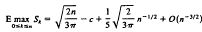 ,
,
where c = 0.297952.... This estimate applies to the problem of packing n rectangles into a unit-width strip; in particular, it makes much more precise the known upper bound on the expected minimum height, 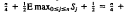 O(n½), when the rectangle sides are 2n independent uniform random draws from [0,1].
O(n½), when the rectangle sides are 2n independent uniform random draws from [0,1].
