A model is proposed for the one-dimensional spectrum and streamwise Reynolds stress in pipe flow for arbitrarily large Reynolds numbers. Constructed in wavenumber space, the model comprises four principal contributions to the spectrum: streaks, large-scale motions, very-large-scale motions and incoherent turbulence. It accounts for the broad and overlapping spectral content of these contributions from different eddy types. The model reproduces well the broad structure of the premultiplied one-dimensional spectrum of the streamwise velocity, although the bimodal shape that has been observed at certain wall-normal locations, and the  $-5/3$ slope of the inertial subrange, are not captured effectively because of the simplifications made within the model. Regardless, the Reynolds stress distribution is well reproduced, even within the near-wall region, including key features of wall-bounded flows such as the Reynolds number dependence of the inner peak, the formation of a logarithmic region, and the formation of an outer peak. These findings suggest that many of these features arise from the overlap of energy content produced by both inner- and outer-scaled eddy structures combined with the viscous-scaled influence of the wall. The model is also used to compare with canonical turbulent boundary layer and channel flows, and despite some differences being apparent, we speculate that with only minor modifications to its coefficients, the model can be adapted to these flows as well.
$-5/3$ slope of the inertial subrange, are not captured effectively because of the simplifications made within the model. Regardless, the Reynolds stress distribution is well reproduced, even within the near-wall region, including key features of wall-bounded flows such as the Reynolds number dependence of the inner peak, the formation of a logarithmic region, and the formation of an outer peak. These findings suggest that many of these features arise from the overlap of energy content produced by both inner- and outer-scaled eddy structures combined with the viscous-scaled influence of the wall. The model is also used to compare with canonical turbulent boundary layer and channel flows, and despite some differences being apparent, we speculate that with only minor modifications to its coefficients, the model can be adapted to these flows as well.
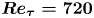 $\boldsymbol {{Re}_\tau = 720}$
$\boldsymbol {{Re}_\tau = 720}$