Suppose each permutation (πl,…,πn) of ( 1, …, n) has probability 1/n!. The oscillation of (πl; …, πn) is defined as Tn = 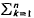 | πk − πk+1|, where πn+1 = π1. It is proved that (Tn − ETn)/(var Tn)1/2 converges in distribution to N(0,1). The connection between the oscillation and the presortedness measure is also discussed.
| πk − πk+1|, where πn+1 = π1. It is proved that (Tn − ETn)/(var Tn)1/2 converges in distribution to N(0,1). The connection between the oscillation and the presortedness measure is also discussed.