The bootstrap current in stellarators can be presented as a sum of a collisionless value given by the Shaing–Callen asymptotic formula and an off-set current, which non-trivially depends on plasma collisionality and radial electric field. Using NEO-2 modeling, analytical estimates and semi-analytical studies with the help of a propagator method, it is shown that the off-set current in the 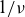$1/\nu$ regime does not converge with decreasing collisionality 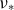$\nu _\ast$ but rather shows oscillations over 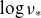$\log \nu _\ast$ with an amplitude of the order of the bootstrap current in an equivalent tokamak. The convergence to the Shaing–Callen limit appears in regimes with significant orbit precession, in particular, due to a finite radial electric field, where the off-set current decreases as 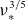$\nu _\ast ^{3/5}$. The off-set current strongly increases in case of nearly aligned magnetic field maxima on the field line where it diverges as 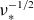$\nu _\ast ^{-1/2}$ in the 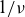$1/\nu$ regime and saturates due to the precession at a level exceeding the equivalent tokamak value by 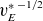${v_E^\ast }^{-1/2}$, where 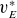$v_E^\ast$ is the perpendicular Mach number. The latter off-set, however, can be minimized by further aligning the local magnetic field maxima and by fulfilling an extra integral condition of “equivalent ripples” for the magnetic field. A criterion for the accuracy of this alignment and of ripple equivalence is derived. In addition, the possibility of the bootstrap effect at the magnetic axis caused by the above off-set is also discussed.

We present orbit classification schemes for use as fast metrics for fusion alpha particle losses implemented in the symplectic guiding-centre code SIMPLE. Two variants respectively based on conservation of the parallel adiabatic invariant, and topology of footprints in Poincaré sections are introduced. Like an existing approach based on the Minkowski fractal dimension, those methods estimate whether a guiding-centre orbit is regular and therefore expected to be confined for infinite time in the collisionless case, or chaotic, which might lead to its loss. Compared with the existing approach, the required orbit tracing time for the novel classifiers is shorter by at least an order of magnitude. This enables massive sampling of orbits across the whole phase space to identify regular and chaotic regions for the purpose stellarator optimization. Based on conservation of the perpendicular invariant, we demonstrate how extended regular regions may act as radial barriers for orbits from the chaotic regions on the radially inboard side. We propose to use a quantified version of this property as a new metric for collisionless fusion alpha losses. As pitch-angle scattering becomes only relevant after alphas have already deposited a significant fraction of their energy, such a metric remains useful also for the case with collisions. This is illustrated by comparison with collisional loss computations. Results are presented for applications to two quasi-isodynamic configurations, a quasi-helical configuration and two quasi-axisymmetric configurations. In addition, the Hamiltonian action-angle formalism is used in quasi-axisymmetric configurations to investigate the overlap of drift-orbit resonances leading to chaos. The respective analysis is performed with the NEO-RT code originally developed for investigation of neoclassical toroidal viscous torque in tokamak plasmas.

Accelerated statistical computation of collisionless fusion alpha particle losses in stellarator configurations is presented based on direct guiding-centre orbit tracing. The approach relies on the combination of recently developed symplectic integrators in canonicalized magnetic flux coordinates and early classification into regular and chaotic orbit types. Only chaotic orbits have to be traced up to the end, as their behaviour is unpredictable. An implementation of this technique is provided in the code SIMPLE (symplectic integration methods for particle loss estimation, Albert et al., 2020b, doi:10.5281/zenodo.3666820). Reliable results were obtained for an ensemble of 1000 orbits in a quasi-isodynamic, a quasi-helical and a quasi-axisymmetric configuration. Overall, a computational speed up of approximately one order of magnitude is achieved compared to direct integration via adaptive Runge–Kutta methods. This reduces run times to the range of typical magnetic equilibrium computations and makes direct alpha particle loss computation adequate for use within a stellarator optimization loop.