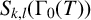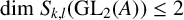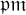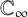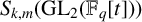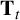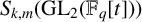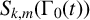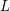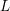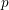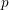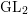Refine search
Actions for selected content:
6 results
NORMAL BASES FOR FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 06 May 2024, pp. 44-55
- Print publication:
- August 2024
-
- Article
- Export citation
NOTES ON ATKIN–LEHNER THEORY FOR DRINFELD MODULAR FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 15 November 2022, pp. 50-68
- Print publication:
- August 2023
-
- Article
- Export citation
HECKE OPERATORS AND DRINFELD CUSP FORMS OF LEVEL
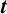 $\boldsymbol {t}$
$\boldsymbol {t}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 15 June 2022, pp. 184-195
- Print publication:
- April 2023
-
- Article
- Export citation
Arithmetic of positive characteristic
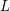 $L$-series values in Tate algebras
$L$-series values in Tate algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 07 September 2015, pp. 1-61
- Print publication:
- January 2016
-
- Article
- Export citation
Hecke characters associated to Drinfeld modular forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 11 / November 2015
- Published online by Cambridge University Press:
- 01 June 2015, pp. 2006-2058
- Print publication:
- November 2015
-
- Article
- Export citation
K1 of products of Drinfeld modular curves and special values of L-functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 4 / July 2010
- Published online by Cambridge University Press:
- 08 June 2010, pp. 886-918
- Print publication:
- July 2010
-
- Article
-
- You have access
- Export citation