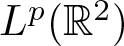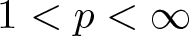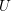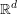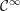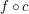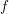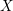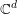Refine search
Actions for selected content:
7 results
Perron’s capacity of random sets
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 01 September 2023, pp. 960-970
-
- Article
- Export citation
ON SEPARATE CONTINUITY AND SEPARATE CONVEXITY: A SYNTHETIC TREATMENT FOR FUNCTIONS AND SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 17 July 2023, pp. 541-551
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A dichotomy of sets via typical differentiability
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 04 November 2020, e41
-
- Article
-
- You have access
- Open access
- Export citation
AN ALTERNATIVE APPROACH TO FRÉCHET DERIVATIVES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 14 May 2020, pp. 202-220
- Print publication:
- October 2021
-
- Article
- Export citation
Arc-smooth functions on closed sets
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 4 / April 2019
- Published online by Cambridge University Press:
- 15 March 2019, pp. 645-680
- Print publication:
- April 2019
-
- Article
- Export citation
METRIC DIFFERENTIABILITY OF LIPSCHITZ MAPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 15 October 2013, pp. 25-35
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
Curves of infinite length in labyrinth fractals
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 30 March 2011, pp. 329-344
-
- Article
-
- You have access
- Export citation