We investigate different geometrical properties, related to Carleson measures and pseudo-hyperbolic separation, of inhomogeneous Poisson point processes on the unit disk. In particular, we give conditions so that these random sequences are almost surely interpolating for the Hardy, Bloch or weighted Dirichlet spaces.

Classical results about peaking from complex interpolation theory are extended to polynomials on a closed disk, and on the complement of its interior. New results are obtained concerning interpolation by univalent polynomials on a Jordan domain whose boundary satisfies certain smoothness conditions.

This paper presents an approach, based on interpolation theory of operators, to the study of interpolating sequences for interpolation Banach spaces between Hardy spaces. It is shown that the famous Carleson result for H∞ can be lifted to a large class of abstract Hardy spaces. A description is provided of the range of the Carleson operator defined on interpolation spaces between the classical Hardy spaces in terms of uniformly separated sequences. A key role in this description is played by some general interpolation results proved in the paper. As by-products, novel results are obtained which extend the Shapiro–Shields result on the characterisation of interpolation sequences for the classical Hardy spaces Hp. Applications to Hardy–Lorentz, Hardy–Marcinkiewicz and Hardy–Orlicz spaces are presented.

We present a new connection between the Hele-Shaw flow, also known as two-dimensional Laplacian growth, and the theory of holomorphic discs with boundary contained in a totally real submanifold. Using this, we prove short-time existence and uniqueness of the Hele-Shaw flow with varying permeability both when starting from a single point and also when starting from a smooth Jordan domain. Applying the same ideas, we prove that the moduli space of smooth quadrature domains is a smooth manifold whose dimension we also calculate, and we give a local existence theorem for the inverse potential problem in the plane.

We complete the investigation of growth properties of analytic functions connected with the Nevanlinna parametrization of the solutions of an indeterminate strong Hamburger moment problem.

Hilbert spaces of analytic functions generated by rotationally symmetric measures on disks and annuli are studied. A domination relation between function norm and weighted sums of integral means on circles is developed. The function norm and the weighted sum take the same value for a specified class of polynomials. This class can be varied according to two parameters. Parts of the construction carry over to other Banach spaces of analytic of harmonic functions. Counterexamples illuminating properties of the complex method of interpolation appear as a byproduct.

In this paper, we consider a class of strong symmetric distributions, which we refer to as the strong c-symmetric distributions. We provide, as the main result of this paper, conditions satisfied by the recurrence relations of certain polynomials associated with these distributions.

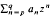Methods from the theory of orthogonal polynomials are extended to L-polynomials . By this means the authors and W. B. Jones (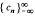J. Math. Anal. Appl. 98 (1984), 528–554) solved the strong Hamburger moment problem, that is, given a double sequence , to find a distribution function ψ(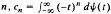t), non-decreasing, with an infinitenumber of points of increase and bounded on −∞ < t < ∞, such that for all integers . In this article further menthods such as analogues of the Lioville-Ostrogradski formula and of the Christoffel-Darboux formula are developed to investigated When the moment porblem has a unique solution. This will be the case if and only if a sequence of nested disks associated with the sequence 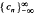has only a point as its intersection (the so called limit point case).