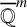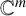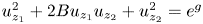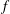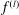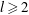Refine search
Actions for selected content:
6 results
Entire solutions of product type nonlinear partial differential equations in
 $\mathbb{C}^n$
$\mathbb{C}^n$
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 12 August 2025, pp. 1-6
-
- Article
- Export citation
Characterization of continuous homomorphisms on entire slice monogenic functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 17 May 2024, pp. 892-920
-
- Article
- Export citation
ON THE EXCEPTIONAL SET OF TRANSCENDENTAL ENTIRE FUNCTIONS IN SEVERAL VARIABLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 20 October 2023, pp. 64-71
- Print publication:
- August 2024
-
- Article
- Export citation
Entire solutions of a variation of the eikonal equation and related PDEs
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 3 / August 2020
- Published online by Cambridge University Press:
- 07 May 2020, pp. 697-708
-
- Article
- Export citation
THE TUMURA–CLUNIE THEOREM IN SEVERAL COMPLEX VARIABLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 13 June 2014, pp. 444-456
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Multidimensional Volterra integral equations of convolution type
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 27 / Issue 3 / May 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 305-312
- Print publication:
- May 1979
-
- Article
-
- You have access
- Export citation