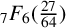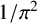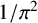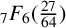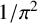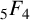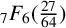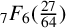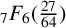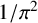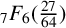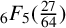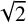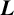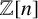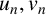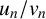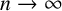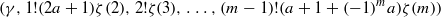Refine search
Actions for selected content:
6 results
THE WZ METHOD AND FLAWLESS WZ PAIRS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 28 April 2025, pp. 1-9
-
- Article
- Export citation
ON GUILLERA’S
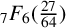 ${}_{7}F_{6}( \frac {27}{64} )$-SERIES FOR
${}_{7}F_{6}( \frac {27}{64} )$-SERIES FOR 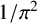 ${1}/{\pi ^2}$
${1}/{\pi ^2}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 09 February 2023, pp. 464-471
- Print publication:
- December 2023
-
- Article
- Export citation
APÉRY LIMITS FOR ELLIPTIC
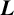 $\boldsymbol {L}$-VALUES
$\boldsymbol {L}$-VALUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 19 January 2022, pp. 273-279
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A MAGNETIC DOUBLE INTEGRAL
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 18 February 2019, pp. 9-25
- Print publication:
- August 2019
-
- Article
-
- You have access
- Open access
- Export citation
RANDOM WALKS, ELLIPTIC INTEGRALS AND RELATED CONSTANTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 26 November 2013, pp. 166-167
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
RATIONAL APPROXIMATIONS TO VALUES OF BELL POLYNOMIALS AT POINTS INVOLVING EULER’S CONSTANT AND ZETA VALUES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 15 June 2012, pp. 71-98
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation